最大連通子數組

這次是求聯通子數組的求和，我們想用圖的某些算法，比如迪杰斯特拉等，但是遇到了困難。用BFS搜索能達到要求，但是還未能成功。

??? 那么我們這樣想，先將每行的最大子數組之和，然后再將這些最大之和組成一個數組，在進行求和，這樣就保證了，加入中間一行為負數，再進行篩選。增加了直接相加的正確率。

??? 實現代碼：

#include <iostream>
#include <fstream>
using namespace std;
int Max(int Array[],int length) { int maxSumOfArray,maxSum; int first=0,last=1; maxSumOfArray=maxSum=Array[0]; //當我們加上一個正數時，和會增加；當我們加上一個負數時，和會減少。 //如果當前得到的和是個負數，那么這個和在接下來的累加中應該拋棄并重新清零，不然的話這個負數將會減少接下來的和。 for(int i=1;i<length;i++) { maxSumOfArray=max(maxSumOfArray+Array[i],Array[i]); //變量maxSumOfArray 為包含Array[i] 與Array[i] 取最大 maxSum=max(maxSum,maxSumOfArray); ////變量maxSum 為maxSum 與 maxSumOfArray 取最大  } cout<<"最大子數組和："<<maxSum<<endl; return maxSum; } int main() { int a; int i=0,j=0; int b[10][10],c[10]; FILE * fp1 = fopen("E:\\input.txt", "r");//打開輸入文件 if (fp1==NULL) {//若打開文件失敗則退出 puts("不能打開文件！"); return 0; } int M,N; fscanf(fp1,"%d",&a); M=a; //行 cout<<"行數:"<<M<<endl; fscanf(fp1,"%d",&a); N=a; //列 cout<<"列數:"<<N<<endl; for (i=0;i<M;i++) { for(j=0;j<N;j++) { if(fscanf(fp1,"%d",&a)==1) { b[i][j]=a; cout<<b[i][j]<<" "; } } cout<<endl; } cout<<"文件已經讀取到第 "<<ftell(fp1)<<" 個偏移字節"<<endl;//輸出fp1指針當前位置相對于文件首的偏移字節數 fclose(fp1);//關閉輸入文件 int thismax[10]; //存放數組每行的最大子數組 cout<<"每行的最大數組和："<<endl; for(i=0;i<M;i++) { for(j=0;j<N;j++) { c[j]=b[i][j]; } thismax[i]=Max(c,N); } cout<<"每行的最大子數組之和再求和"<<endl; int sum=Max(thismax,M); //每行作為一個數組再求最大的子數組和 cout<<"最大聯通子數組的和為："<<sum<<endl; return 0; }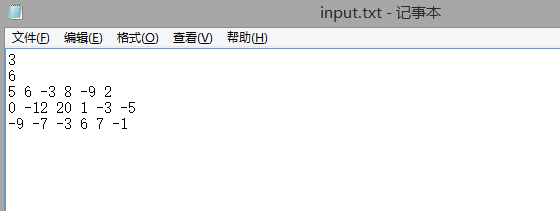

這種方法只能在某些情況下可以實現，更加完整的我們還在完善。

隊友 于磊http://www.cnblogs.com/cnyulei/