? ? ? ? 給定一個不含重復數字的整數數組?
nums?,返回其?所有可能的全排列?。可以?按任意順序?返回答案。輸入:nums = [1,2,3] 輸出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
先在這里說明一下排列和組合的區別?
組合:是指從一個元素集合中選擇出若干個元素,形成一個無序的子集,組合不考慮元素的順序,只關注元素的選擇
排列:是指從一個元素集合中選擇出若干元素,形成一個有序的序列。排列關注元素的順序。
簡單的來說,就是排列是元素是有序的,組合是無序的
一般排列組合問題我們都可以看成是一棵樹(每個元素不允許重復)? ? ? ? ? ?
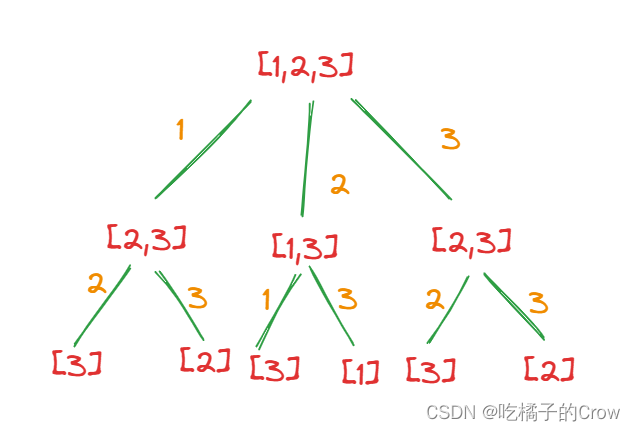
因為我們這題要求的是不重復的排列數,所以我們的模板就可以套了(模板必須要記的——理解)
//不含重復元素的排列數
void backTrack(int[] nums){1for(int i=0;i<nums.length;i++){if(uesd[i])continue;used[i]=true;path.addLast(nums[i]);backTrack(nums);path.removeLast(nums[i]);used[i]=false;}源代碼如下:
//存儲結果集List<List<Integer>> list = new ArrayList<>();//路徑Deque<Integer> path = new LinkedList<>();//是否被訪問boolean[] visited = null;public List<List<Integer>> permute(int[] nums) {//對入參進行判斷if (nums == null || nums.length == 0) {return list;}//對數組進行初始化visited=new boolean[nums.length];//開始遞歸,因為是排列,后面的元素也有可能在前面的元素前面,所以不需要傳遞索引backtracking(nums);//返回結果集return list;}private void backtracking(int[] nums) {//找到滿足條件得到一種情況,存入結果集中if (path.size()== nums.length) {list.add(new ArrayList<>(path));return;}//遍歷每一個元素for (int j = 0; j < nums.length; j++) {//如果被訪問過,直接跳過,避免重復選擇if(visited[j]){continue;}path.add(nums[j]);visited[j]=true;backtracking(nums);//回溯path.removeLast();visited[j]=false;}
}在這里給大家提供我刷組合排列問題總結的模板:
組合子集問題每個元素的相對位置已經固定,所以每次去枚舉的時候都是從自身的右側開始枚舉
排列問題的每個元素的相對位置是不固定的。左側的元素可能會出現在右側,故每次每次枚舉都是從0位置上開始枚舉的
-
元素無重不可復選(nums中的元素唯一,每個元素最多只能被使用一次)
/*組合/子集問題回溯模板*/
/* [1,2,3] */
void backTrack(int[] nums,int start){//順序無關,每次從自身的右邊開始for(int i=start;i<nums.length;i++){path.addLast(nums[i]);backTrack(nums,i+1);path.removeLast(nums[i]);}
}
/* 排列問題回溯模板*/
void backTrack(int[] nums){//順序有關,每次從0開始for(int i=0;i<nums.length;i++){if(uesd[i])continue;used[i]=true;path.addLast(nums[i]);backTrack(nums);path.removeLast(nums[i]);used[i]=false;}
}-
.元素可重不可復選(nums中的元素可以存在重復,每個元素最多只能被使用一次)
Arrays.sort(nums); /* 組合/子集問題回溯算法框架 */ void backtrack(int[] nums, int start) {// 回溯算法標準框架for (int i = start; i < nums.length; i++) {// 剪枝邏輯,跳過值相同的相鄰樹枝if (i > start && nums[i] == nums[i - 1]) {continue;}// 做選擇track.addLast(nums[i]);// 注意參數backtrack(nums, i + 1);// 撤銷選擇track.removeLast();} }Arrays.sort(nums); /* 排列問題回溯算法框架 */ void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 剪枝邏輯if (used[i]) {continue;}// 剪枝邏輯,固定相同的元素在排列中的相對位置if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;}// 做選擇used[i] = true;track.addLast(nums[i]);backtrack(nums);// 撤銷選擇track.removeLast();used[i] = false;} }
有很多人對上述剪枝操作不理解,看了這幅圖你就會豁然開?
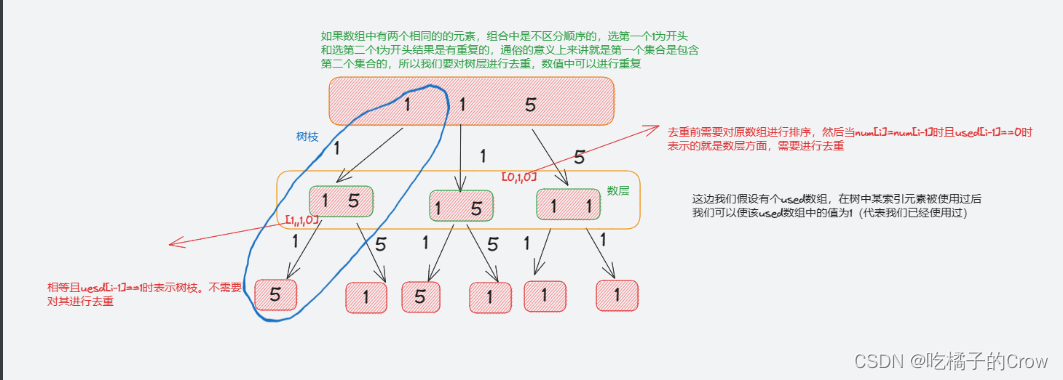
-
元素無重可復選(nums中的元素都是唯一的,每個元素可以被使用若干次)
/* 組合/子集問題回溯算法框架 */ void backtrack(int[] nums, int start) {// 回溯算法標準框架for (int i = start; i < nums.length; i++) {// 做選擇track.addLast(nums[i]);// 可以復選,所以i不用+1作為參數backtrack(nums, i);// 撤銷選擇track.removeLast();} }/* 排列問題回溯算法框架 */ void backtrack(int[] nums) {for (int i = 0; i < nums.length; i++) {// 做選擇track.addLast(nums[i]);backtrack(nums);// 撤銷選擇track.removeLast();} }

)















)

)