1.案例背景
????????一般神經網絡中所包含的網絡輸人數據是研究者根據專業知識和經驗預先選擇好的,然而在許多實際應用中,由于沒有清晰的理論依據,神經網絡所包含的自變量即網絡輸入特征難以預先確定,如果將一些不重要的自變量也引入神經網絡,會降低模型的精度,因此選擇有意義的自變量特征作為網絡輸入數據常常是應用神經網絡分析預測問題中很關鍵一步。選擇神經網絡輸入的方法有多種,其基本思路是:盡可能將作用效果顯著的自變量選入神經網絡模型中,將作用不顯著的自變量排除在外。本例將結合BP神經網絡應用平均影響值(Mean Impact Value,MIV)算法來說明如何使用神經網絡來篩選變量,找到對結果有較大影響的輸人項,繼而實現使用神經網絡進行變量篩選。
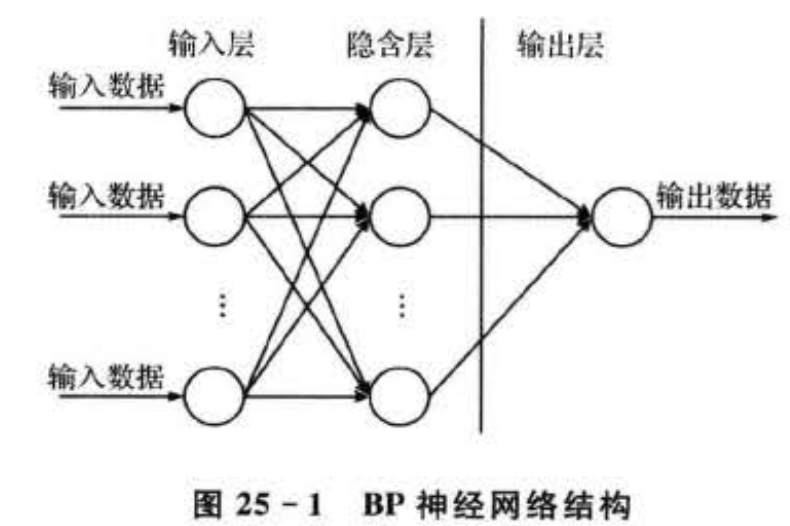
????????BP(back propagation)神經網絡是一種神經網絡學習算法,其全稱為基于誤差反向傳播算法的人工神經網絡。圖25-1所示為單隱藏層前饋網絡拓撲結構,一般稱為三層前饋網或三層感知器,即輸入層,中間層(也稱隱藏層)和輸出層。輸入層各神經元負責接收來自外界的輸入信息,并傳遞給中間層各神經元;中間層是內部信息處理層,可以設計為單隱層或者多隱層結構;最后一個隱層傳遞到輸出層各神經元的信息,經進一步處理后,完成一次學習的正向傳播處理過程,由輸出層向外界輸出信息處理結果。BP神經網絡的特點是:各層神經元僅與相鄰層神經元之間相互全連接,同層內神經元之間無連接,各層神經元之間無反饋連接,構成具有層次結構的前饋型神經網絡系統。單層前饋神經網絡只能求解線性可分問題,能夠求解非線性問題的網絡必須是具有隱層的多層神經網絡。當實際輸出與期望輸出不符時,進入誤差的反向傳播階段。誤差通過輸出層,按誤差梯度下降的方式修正各層權值,向隱層、輸入層逐層反傳。周而復始的信息正向傳播和誤差反向傳播過程,是各層權值不斷調整的過程,也是神經網絡學習訓練的過程,此過程一直進行到網絡輸出的誤差減少到可以接受的程度﹐或者預先設定的學習次數為止。
????????Dombi等人提出用MIV來反映神經網絡中權重矩陣的變化情況,MIV被認為是在神經網絡中評價變量相關性最好的指標之一,也為解決此類問題開創了新思路。因此探索此類型的評價指標在實際工作中的運用以及尋找新的評價指標是值得研究的課題。
????????本例選擇MIV作為評價各個自變量對于因變量影響的重要性大小指標。MIV是用于確定輸人神經元對輸出神經元影響大小的一個指標,其符號代表相關的方向,絕對值大小代表影響的相對重要性。具體計算過程:在網絡訓練終止后,將訓練樣本P中每一自變量特征在其原值的基礎上分別加和減10%構成兩個新的訓練樣本P,和P. ,將P,和P:分別作為仿真樣本利用已建成的網絡進行仿真,得到兩個仿真結果A和A,求出A和A2的差值,即為變動該自變量后對輸出產生的影響變化值(Impact Value,1V),最后將IⅣ按觀測例數平均得出該自變量對于應變量——網絡輸出的MIV。按照上面步驟依次算出各個自變量的MIV值,最后根據MIV絕對值的大小為各自變量排序,得到各自變量對網絡輸出影響相對重要性的位次表,從而判斷出輸入特征對于網絡結果的影響程度,即實現了變量篩選。
2.模型建立
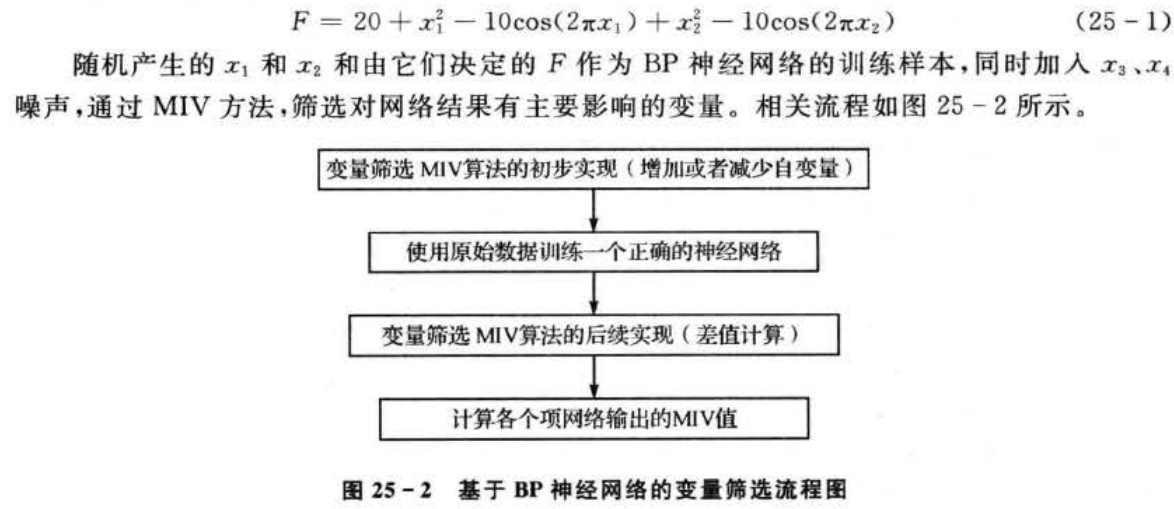
????????本例產生網絡訓練數據的方法如下:
3.MATLAB實現
?
%% 清空環境變量
clc
clear
%% 產生輸入 輸出數據% 設置步長
interval=0.01;% 產生x1 x2
x1=-1.5:interval:1.5;
x2=-1.5:interval:1.5;% 產生x3 x4(噪聲)
x=rand(1,301);
x3=(x-0.5)*1.5*2;
x4=(x-0.5)*1.5*2;% 按照函數先求得相應的函數值,作為網絡的輸出。
F =20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);%設置網絡輸入輸出值
p=[x1;x2;x3;x4];
t=F;%% 變量篩選 MIV算法的初步實現(增加或者減少自變量)p=p';
[m,n]=size(p);
yy_temp=p;% p_increase為增加10%的矩陣 p_decrease為減少10%的矩陣
for i=1:np=yy_temp;pX=p(:,i);pa=pX*1.1;p(:,i)=pa;aa=['p_increase' int2str(i) '=p;'];eval(aa);
endfor i=1:np=yy_temp;pX=p(:,i);pa=pX*0.9;p(:,i)=pa;aa=['p_decrease' int2str(i) '=p;'];eval(aa);
end%% 利用原始數據訓練一個正確的神經網絡
nntwarn off;
p=yy_temp;
p=p';
% bp網絡建立
net=newff(minmax(p),[8,1],{'tansig','purelin'},'traingdm');
% 初始化bp網絡
net=init(net);
% 網絡訓練參數設置
net.trainParam.show=50;
net.trainParam.lr=0.05;
net.trainParam.mc=0.9;
net.trainParam.epochs=2000;% bp網絡訓練
net=train(net,p,t);%% 變量篩選 MIV算法的后續實現(差值計算)% 轉置后simfor i=1:neval(['p_increase',num2str(i),'=transpose(p_increase',num2str(i),');'])
endfor i=1:neval(['p_decrease',num2str(i),'=transpose(p_decrease',num2str(i),');'])
end% result_in為增加10%后的輸出 result_de為減少10%后的輸出
for i=1:neval(['result_in',num2str(i),'=sim(net,','p_increase',num2str(i),');'])
endfor i=1:neval(['result_de',num2str(i),'=sim(net,','p_decrease',num2str(i),');'])
endfor i=1:neval(['result_in',num2str(i),'=transpose(result_in',num2str(i),');'])
endfor i=1:neval(['result_de',num2str(i),'=transpose(result_de',num2str(i),');'])
end%% MIV的值為各個項網絡輸出的MIV值 MIV被認為是在神經網絡中評價變量相關的最好指標之一,其符號代表相關的方向,絕對值大小代表影響的相對重要性。for i=1:nIV= ['result_in',num2str(i), '-result_de',num2str(i)];eval(['MIV_',num2str(i) ,'=mean(',IV,')'])end
????????運行結果如下:
MIV_1 =1.2030MIV_2 =1.0120MIV_3 =-0.0376MIV_4 =0.0773????????MIV_n的值為各項網絡輸出的MIV值,MIV被認為是在神經網絡應用中評價變量對結果影響大小的最好指標之一,其符號代表相關的方向,絕對值大小代表影響的相對重要性。
????????由此可見;第一,二個變量得出的MIV值較大;因為F值是靠x1?,x2計算出來的,與x3 ,x4無關,所以MIV篩選出的對結果有重要影響的自變量同真實情況一致。神經網絡使用MIV方法對變量進行篩選是可行的。
4.案例擴展
????????神經網絡模型本身可以應用于多重共線性的數據,所謂多重共線性(multicollinearity)是指回歸模型中的自變量之間由于存在精確相關關系或高度相關關系而使模型估計失真或難以估計準確。為了網絡的訓練效果更佳,使用了MIV算法來尋找對結果影響大的變量。不只是BP神經網絡,其他很多神經網絡在進行擬合,回歸,分類的條件下,都可以應用MIV算法進行變量篩選并且建立自變量更少.效果更好的神經網絡模型。



)
)



)










