In short, the Diffie Hellman is a widely used technique for securely sending a symmetric encryption key to another party. Before proceeding, let’s discuss why we’d want to use something like the Diffie Hellman in the first place. When transmitting data over the Internet as plain text, it’s easy for someone to use some kind of packet sniffer like WireShark to capture packets. A malicious person, could listen in on the conversation you had with your girlfriend or worse yet, steals passwords and credit card information. Fortunately, some very smart people came up with a way to encode information for transit. The process by which we convert ordinary plain text into something unintelligible and vice-versa is known as cryptography. The most basic example of cryptography is called the Caesar Cypher.

簡而言之，Diffie Hellman是一種用于將對稱加密密鑰安全發送給另一方的廣泛使用的技術。 在繼續之前，讓我們討論為什么首先要使用Diffie Hellman之類的東西。 當以純文本格式在Internet上傳輸數據時，對于某人來說，使用諸如WireShark之??類的數據包嗅探器來捕獲數據包很容易。 惡意軟件的人可能會收聽您與女友的交談，甚至更糟，他們會竊取密碼和信用卡信息。 幸運的是，一些非常聰明的人想出了一種方法來編碼信息以進行運輸。 我們將普通的純文本轉換為難以理解的過程的過程，反之亦然，即密碼術 。 密碼學的最基本示例稱為凱撒密碼。

In essence, both parties have a symmetric key which specifies what characters map to what symbol of the encrypted text. Those who don’t possess the key cannot read the message. For example, in the preceding image, the character ‘A’ would be encoded as a ‘T’ in the encrypted message. An individual on the receiving end could then use the same Caesar Cypther to decode the message.

本質上，雙方都有一個對稱密鑰，它指定哪些字符映射到加密文本的什么符號。 那些沒有鑰匙的人無法閱讀消息。 例如，在前面的圖像中，字符“ A”在加密消息中將被編碼為“ T”。 然后，接收端的個人可以使用相同的Caesar Cypther對消息進行解碼。

In the realm of computer networking, the problem with symmetric encryption algorithms is that the key must be inevitably be sent over the network to the other party so that they can decrypt incoming messages, and encrypt them in turn. If a malicious actor happened to be listening to the network at that point in time, they could obtain the key, and use it for nefarious purposes.

在計算機網絡領域，對稱加密算法的問題在于必須將密鑰不可避免地通過網絡發送給另一方，以便他們可以解密傳入的消息并依次對其進行加密。 如果惡意行為者恰好在該時間點正在偵聽網絡，則他們可以獲得密鑰，并將其用于惡意目的。

This is where asymmetrical encryption comes in to play. Asymmetrical encryption works by generating a public and private key pair. The public key can only be used to encrypt messages whereas the private key can only be used to decrypt messages. For example, when you do your online banking, you give the bank your public key which is then used to encrypt the data sent back to you. If a bad guy gets their hands on the public key, they can’t do any real harm since they only have the ability to encrypt data.

這就是非對稱加密發揮作用的地方。 非對稱加密通過生成公鑰和私鑰對來工作。 公鑰只能用于加密消息，而私鑰只能用于解密消息。 例如，當您進行在線銀行業務時，您給銀行您的公共密鑰，然后將其用于加密發送回給您的數據。 如果一個壞人得到了公鑰，那么他們就不會造成任何真正的傷害，因為他們只能加密數據。

Today, the most widely used asymmetrical encryption algorithm is RSA. RSA stands for Rivest–Shamir–Adleman after the people who first described the algorithm back in 1977. The RSA algorithm encrypts messages by raising the message to the power of the public key and then taking the modulo of the result. To decrypt a given message, we raise it to the power of the private key and then take the modulo of the result. RSA relies on a mathematical concept known as a one-way function. Suppose we had the following equation:

如今，使用最廣泛的非對稱加密算法是RSA。 在此之后，RSA代表Rivest–Shamir–Adleman 最早是在1977年對算法進行描述的人們。RSA算法通過將消息提升為公鑰的能力然后對結果取模來對消息進行加密。 為了解密給定的消息，我們將其提升為私鑰的能力，然后對結果取模。 RSA依賴于稱為單向函數的數學概念。 假設我們有以下等式：

Now, say you were given the number 8 and asked to get back to 23. Could you do it?

現在，假設您得到的數字為8，并要求返回23 。 你能做到嗎？

It’s relatively easy to work our way backwards in order figure out all the factors of 8.

找出8的所有因素，倒退比較容易。

In contrast, the modulo (synonymous with remainder) operation is an example of a one-way function. Suppose we had the following equation:

相反，取模(與余數同義)操作是單向函數的一個示例。 假設我們有以下等式：

If you were asked to derive 11 from 3, could you do it?

如果要求您從3導出11 ，您可以這樣做嗎？

You may be able to obtain the correct answer (11) by trying out all the different possibilities (i.e. 3 % 4 = 3, 7 % 4 = 3, 11 % 4 = 3), but when the numerator is very large, as in the case of RSA (i.e. 4096 bits long), there are a lot and I mean A LOT of permutations that give a remainder of 3. Given this property, hackers would have no choice but to use brute force (try every possibility) to determine the private key from the encrypted message and public key. Given that today’s keys are 4096 bits long, it would take traditional computers centuries to go through all the possible values.

通過嘗試所有不同的可能性(例如3％4 = 3，7％4 = 3，11％4 = 3) ，您可能能夠獲得正確的答案( 11 ) ，但是當分子很大時，例如對于RSA(即4096位長)的情況，有很多，我的意思是說，很多置換提供剩余的3。給定此屬性，黑客別無選擇，只能使用蠻力(嘗試各種可能性)來確定加密消息中的私鑰和公鑰。 鑒于今天的密鑰長為4096位，傳統計算機要花所有幾個世紀才能經歷所有可能的值。

In practice, asymmetrical encryption is 3 to 5 orders of magnitude slower than symmetric encryption. Therefore, we don’t encrypt the actual payload using asymmetrical encryption. Rather, we use a technique like Diffie-Hellman to securely send a symmetric encryption key to the other party, and then use said key to encrypt/decrypt all further messages.

實際上，非對稱加密比對稱加密慢3至5個數量級。 因此，我們不會使用非對稱加密來加密實際的有效負載。 相反，我們使用Diffie-Hellman之類的技術將對稱加密密鑰安全地發送給另一方，然后使用所述密鑰對所有其他消息進行加密/解密。

模算術(RSA)Diffie Hellman (Modulo Arithmetic (RSA) Diffie Hellman)

We’ve already described the RSA at a high level. Now, let’s take a look at a concrete example. Suppose, Bob wants to send a message to Alice. Bob will start off by generating a new random prime number N and corresponding generator g.

我們已經在較高層次上描述了RSA。 現在，讓我們看一個具體的例子。 假設，鮑勃想要發送一條消息給愛麗絲。 Bob將通過生成一個新的隨機素數N和相應的生成器g來開始。

NOTE: g isn’t random, but how we go about selecting it is beyond the scope of this article.

注意：g不是隨機的，但是如何選擇它超出了本文的范圍。

In practice, N is a large number. However, for the sake of simplicity, we’ll use the following values:

實際上，N是一個很大的數字。 但是，為簡單起見，我們將使用以下值：

Both g & N are sent over the network as plain text. Bob then generates a secret key a = 2. Next, Bob raises the generator g to the power of his secret key a, and takes the modulo of the result. The end product A = 5 is sent to Alice.

g和N均以純文本形式通過網絡發送。 鮑勃然后生成一個秘密密鑰a = 2 。 接下來，鮑勃將生成器g提升到他的私鑰a的冪，并對結果取模。 最終產品A = 5被發送給Alice。

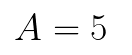
On the other end, Alice performs the same steps — that is, she generates a secret key b, raises the generator g to the power of her secret key b, takes the modulo of the product, and sends the end result B = 3 to Bob.

在另一端，愛麗絲執行相同的步驟-即，她生成一個秘密密鑰b，將生成器g提升為她的秘密密鑰b的冪，取乘積的模，然后將最終結果B = 3發送給鮑勃

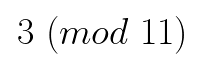
Even if a malicious actor were to snoop on their traffic. They wouldn’t be able to derive Bob’s or Alice’s secret key from A and B.

即使惡意行為者會監聽他們的流量。 他們將無法從A和B導出Bob或Alice的秘密密鑰。

Upon receiving B from Alice, Bob raises it to the power of his private key a, and takes the modulo of the result.

一旦從接收到乙 愛麗絲(Alice)，鮑勃(Bob)將其提升為私鑰a的冪，然后對結果取模。

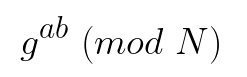
Alice does the same.

愛麗絲也一樣。

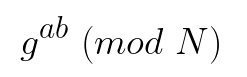
Alice and Bob both end up with the same number, 9, in this case. They then use 9 as the key for a symmetrical encryption algorithm like AES.

在這種情況下，愛麗絲和鮑伯都以相同的數字9結束。 然后，他們使用9作為對稱加密算法(例如AES)的密鑰。

橢圓曲線Diffie Hellman (Elliptic Curve Diffie Hellman)

Trying to derive the private key from a point on an elliptic curve is harder problem to crack than traditional RSA (modulo arithmetic). In consequence, Elliptic Curve Diffie Hellman can achieve a comparable level of security with less bits.

試圖從橢圓曲線上的某個點導出私鑰比傳統的RSA(模算術)更難破解。 因此，橢圓曲線Diffie Hellman可以用更少的位達到可比較的安全級別。

A smaller key requires less computational steps in order to encrypt/decrypt a given payload. You wouldn’t notice much of a difference when establishing secured connections from your local machine. However, on something like a Medium web server that performs thousands upon thousands of key exchanges every second, the use of Elliptic Curve Diffie Hellman can lead to significant savings.

較小的密鑰需要較少的計算步驟才能加密/解密給定的有效負載。 從本地計算機建立安全連接時，您不會注意到很大的不同。 但是，在諸如中型Web服務器這樣每秒執行成千上萬次密鑰交換的事物上，使用橢圓曲線Diffie Hellman可以節省大量資金。

We can visualize the domain of all possible numbers in a Diffie Hellman RSA key exchange as a circle (due to the nature of the modulo function). The larger the value of n, the larger the circle, and the harder it is to guess the correct number.

我們可以將Diffie Hellman RSA密鑰交換中所有可能數字的域可視化為一個圓(由于取模函數的性質)。 n的值越大，圓圈越大，猜測正確的數字就越困難。

In contrast, as the name implies, the domain of all possible numbers for an elliptic curve Diffie Hellman key exchange takes the form of an elliptic curve.

相反，顧名思義，橢圓曲線的所有可能數字的域Diffie Hellman密鑰交換采用橢圓曲線的形式。

The preceding elliptic curve is characterized by the following mathematical equation:

前面的橢圓曲線的特征在于以下數學方程式：

In the wild, it’s pretty common to take use the equation (mod n).

在野外，使用等式( mod n )很常見。

In practice, you want to use curves that have been developed by professional mathematicians, and vetted to ensure they are secure.

在實踐中，您想使用由專業數學家開發并經過審查以確保其安全性的曲線。

Instead of raising things to powers as in the case of RSA, elliptic curve Diffie Hellman works by adding the point G to itself several times over.

橢圓曲線Diffie Hellman并沒有像RSA那樣提高功效，而是通過將G點自身加數倍來工作。

Let’s take a look at an example. Suppose Bob initiates a connection with Alice. Bob selects a generator G (a point on the curve) and the parameters a, b, n of the elliptic curve equation, and sends them across the wire as plain text.

讓我們看一個例子。 假設Bob啟動與Alice的連接。 鮑勃選擇一個生成器G(曲線上的一個點)和橢圓曲線方程的參數a ， b ， n ，并將它們以純文本形式發送到網上。

Bob and Alice then each generate a private key (number). For the sake of simplicity, let’s assume Bob selects b = 9 and Alice selects a = 3. Bob and Alice are responsible for computing bG = 9G and aG = 3G respectively.

然后，Bob和Alice各自生成一個私鑰(數字)。 為了簡單起見，我們假設Bob選擇b = 9并選擇 愛麗絲選擇a = 3 。 Bob和Alice分別負責計算bG = 9G和aG = 3G 。

In order to compute xG (where x is any number), we use the formulas for adding and doubling a point. For instance, to determine 2G, we use the formula for doubling a point.

為了計算xG (其中x是任意數字) ，我們使用公式對一個點進行加法和加倍。 例如，要確定2G，我們使用公式將點加倍。

To take the modulo of a fraction, we can make use of a modular multiplicative inverse calculator.

為了取小數的模，我們可以使用模塊化的乘法逆計算器。

We then multiply the answer with 77 % 17 = 9, and take the modulo of the result.

然后，將答案乘以77％17 = 9，并對結果取模。

The x coordinate of the point can be calculated as follows:

點的x坐標可以如下計算：

We then use x2G to compute y2G.

然后，我們使用x2G計算y2G。

To calculate 3G, we use the formula for adding a point.

為了計算3G，我們使用公式來添加一個點。

We start off by calculating the slope.

我們從計算斜率開始。

Then we compute the x position of the new point.

然后，我們計算新點的x位置。

Finally, we use the value of the x coordinate to compute y.

最后，我們使用x坐標的值來計算y。

Bob sends bG = 9G = (7, 6) over the network. Similarly, Alice sends aG = 3G = (10, 6). In the event, a malicious actor is listening, it’s damn well impossible to derive the value of aG or bG from the points (7, 6) and (10, 6) on the elliptic curve.

鮑勃通過網絡發送bG = 9G =( 7，6 ) 。 類似地，愛麗絲發送aG = 3G =(10，6) 。 如果出現惡意行為者正在監聽的情況，從橢圓曲線上的點( 7，6 )和( 10，6)得出aG或bG的值是絕對不可能的。

Once Bob receives aG = (10 , 6) from Alice, he computes abG = 9(3G) = 27G = (13, 7). When Alice receives bG = (7, 6) from Bob, she computes abG = 3(9G) = 27G = (13, 7). They then both use the x coordinate of abG as their symmetrical encryption key for all further data transfer.

一旦Bob從Alice 收到aG =(10，6 ) ，他就計算abG = 9(3G)= 27G =(13，7) 。 當Alice從Bob收到bG =( 7，6 )時，她計算abG = 3(9G)= 27G =(13，7) 。 然后，它們都將abG的x坐標用作所有進一步數據傳輸的對稱加密密鑰。