Bayes’ Theorem is one of the most known to the field of probability, and it is used often as a baseline model in machine learning. It is, however, too often memorized and chanted by people who don’t really know what P(B|E) = P(E|B) * P(B) / P(E) actually does. This short article will pick apart Bayes’ Theorem and show how it simplifies to an intuitive fraction we all use on a common basis.

貝葉斯定理是概率領域中最著名的定理之一，它經常被用作機器學習中的基線模型。 然而，它經常被那些并不真正知道P(B|E) = P(E|B) * P(B) / P(E)實際工作的人記住和高呼。 這篇簡短的文章將分解貝葉斯定理，并說明如何將其簡化為我們大家共同使用的直觀分數。

First, some basic probability context.

首先，一些基本的概率背景。

The belief is a statement we would like to verify is correct or incorrect, like ‘a person is male’ or ‘a person has long hair’. The evidence is known information about the subject in the belief. Lastly, the | vertical pipe is used as the word ‘given…’. You’ll often see (B|E) as ‘the probability belief B is true, given the evidence E.’

信念是我們要驗證正確或不正確的陳述，例如“一個人是男性”或“一個人有長發”。 證據是有關信念中受試者的已知信息。 最后， | 垂直管道被用作“給定...”一詞。 在給定證據E的情況下，您經常會看到(B|E)為“概率信念B為真”。

Let’s take the following table of students at Hypothetical High School.

讓我們看一下假設高中學生的下表。

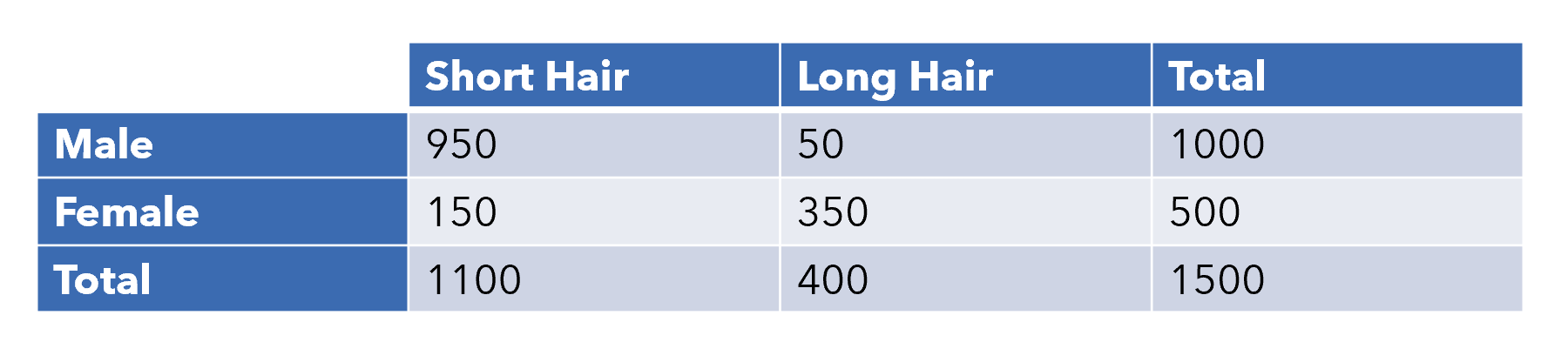
We want to find the probability that a person is female (belief) given long hair (evidence). This can be expressed as (female|long hair). Even without the theorem, this is quite simple to calculate, intuitively. We simply need to divide the number of females who have long hair by the total number of people who have long hair, which is 350/400=0.875.

我們想要找到在長發(證據)下一個人是女性(信念)的概率。 這可以表示為(female|long hair) 。 即使沒有定理，這在直觀上也很容易計算。 我們只需要將長發女性的數量除以長發總數即可，即350/400=0.875 。

It’s worthwhile diving a little into why we have this intuition. Since we know that the person has long hair, we look in the column of ‘Long Hair’ and the two classes within that category (being male or female). Then, our formula is simply people who are female and who have long hair divided by all people who have long hair.

值得深入探討為什么我們有這種直覺。 由于我們知道該人長發，因此我們在“長發”列中查找該類別中的兩個類別(男性或女性)。 那么，我們的公式就是女性，長發的人除以所有長發的人。

Hence, we can confidently say that, if you have long hair, you have a 87.5% chance of being a female at Hypothetical High School.

因此，我們可以自信地說，如果您留著長發，那么在假高中成為女性的可能性為87.5％。

Let’s use Bayes’ Theorem to solve this — and you’ll realize that it is simply putting into rigorously mathematical terms this intuition!

讓我們使用貝葉斯定理來解決這個問題，您會意識到，它只是將這種直覺嚴格地數學化了！

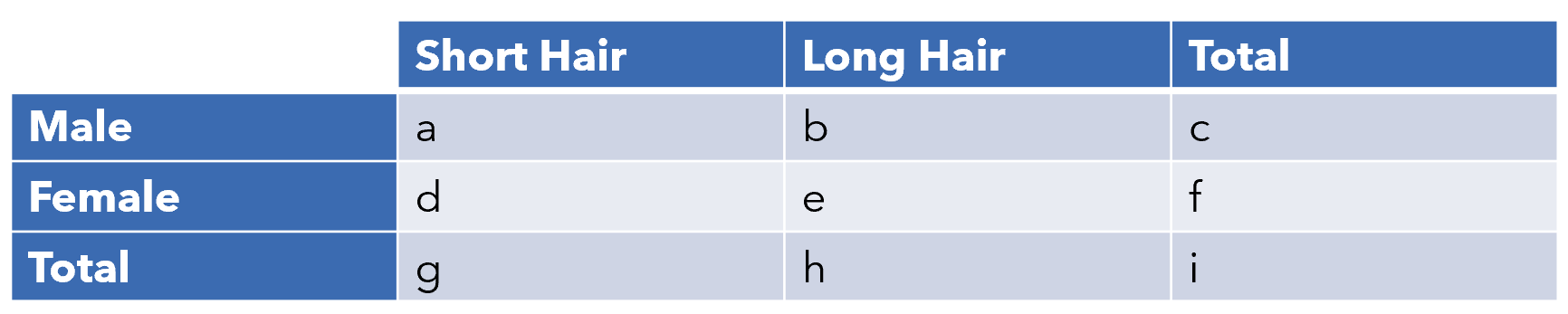
Variable names from a-i will be used to represent different quantities. Remember that our intuitive formula was e/h, or the number of people who are female and have long hair, divided by the total number of people with long hair.

從變量名a - i將被用來代表不同的數量。 請記住，我們的直觀公式是e/h ，即長發的女性人數除以長發總數。

Bayes formula says the following:

貝葉斯公式表示以下內容：

P(B|E) = P(E|B)*P(B) / P(E)

This translates in our scenario to:

在我們的方案中，這意味著：

P(Female|Long Hair) = P(Long Hair|Female)*P(Female)/P(Long Hair)

Let’s represent these using variables. For example, the probability that someone has long hair given that they are female is e/f, since e represents the number of females with long hair and f represents the total number of females. P(Female) is f/i, since f is the number of females and i is the total number of people (males and females).

讓我們使用變量來表示它們。 例如，某人由于是女性而e/f長發的概率為e/f ，因為e代表留長發的女性人數， f代表女性總數。 P(Female)是f/i ，因為f是女性的數量，而i是總人數(男性和女性)。

P(Female|Long Hair) = (e/f)*(f/i) / (h/i) = (e/f)*(f/i)*(i/h)

With some simple algebraic manipulation, we realize that (e/f)*(f/i) results in (e/i), and (e/i)*(i/h) equals (e/h) — our intuitive formula!

通過一些簡單的代數運算，我們意識到(e/f)*(f/i)結果為(e/i) ，而(e/i)*(i/h)等于(e/h) -我們的直觀公式！

So, Bayes’ Theorem is really a roundabout way to express a simple idea. At least in our context of fraction manipulation, P(B) simply serves as a bridge to cancel out reciprocals. So, when use Bayes’ Theorem to calculate P(B|E), you are essentially calculating the following:

因此，貝葉斯定理實際上是表達簡單思想的一種回旋方式。 至少在分數操作的上下文中， P(B)只是充當抵消倒數的橋梁。 因此，當使用貝葉斯定理來計算P(B|E) ，實際上是在計算以下內容：

# items that are B and E / total # items that are E

Bayes’ Theorem is useful for calculating this probability if it is difficult or thorny to directly calculate this by making use of other more accessible probabilities. This can be useful when calculating three separate probabilities is less expensive than calculating one primary one.

如果難以或棘手通過利用其他更容易獲得的概率直接計算此概率，則貝葉??斯定理對于計算該概率很有用。 當計算三個獨立的概率比計算一個主要的概率便宜時，這將很有用。

At a higher level, one may be inclined to say that Bayes’ Theorem reveals relationships in the nature of probability. At a lower — and perhaps more practical — level, Bayes’ Theorem is a clever way to get around directly calculating a probability with other probabilities and chain multiplication.

在更高的層次上，人們可能傾向于說貝葉斯定理揭示了概率性質中的關系。 貝葉斯定理在較低的水平上，也許是在更實際的水平上，是一種聰明的方法，可以直接計算其他概率和鏈乘法的概率。

All images created by author.

作者創作的所有圖像。