給你一個 m x n 的整數矩陣 points （下標從 0 開始）。一開始你的得分為 0 ，你想最大化從矩陣中得到的分數。

你的得分方式為：每一行 中選取一個格子，選中坐標為 (r, c) 的格子會給你的總得分 增加 points[r][c] 。

然而，相鄰行之間被選中的格子如果隔得太遠，你會失去一些得分。對于相鄰行 r 和 r + 1 （其中 0 <= r < m - 1），選中坐標為 (r, c1) 和 (r + 1, c2) 的格子，你的總得分 減少 abs(c1 - c2) 。

請你返回你能得到的 最大 得分。

abs(x) 定義為：

如果 x >= 0 ，那么值為 x 。
如果 x < 0 ，那么值為 -x 。

示例 1：

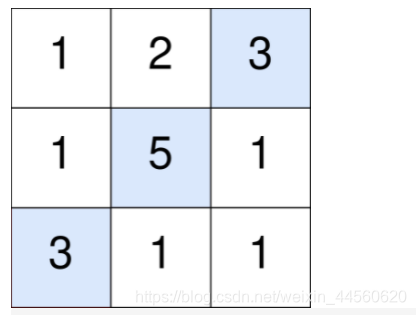
輸入：points = [[1,2,3],[1,5,1],[3,1,1]]
輸出：9
解釋：
藍色格子是最優方案選中的格子，坐標分別為 (0, 2)，(1, 1) 和 (2, 0) 。
你的總得分增加 3 + 5 + 3 = 11 。
但是你的總得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最終得分為 11 - 2 = 9 。

解題思路

數組定義

dp[i]代表在數組的最后一行選擇第i列格子時的最大得分

狀態轉移

dp[i]只由上一行決定，樸素的想法是對于每一個dp[i]都遍歷上一行的所有值，找出減去abs(c1 - c2)最大的那個得分，但是我們可以進行優化只維護上一行中位于i左邊的最大得分lMax和i右邊的最大得分rMax，通過在線性時間內掃描一遍i的同時，維護lMax和rMax，而dp[i]=max(t[i],lMax-1,rMax-1)(t[i]為上一行的dp[i])

代碼

class Solution {public long maxPoints(int[][] points) {int m=points[0].length,n=points.length;long[] dp =new long[m];for (int i=0;i<n;i++){long lMax=0,rMax=0;long[] t = Arrays.copyOf(dp, m);for (int j=0;j<m;j++){lMax=Math.max(lMax-1,dp[j]);t[j]=Math.max(t[j],lMax);}for (int j=m-1;j>=0;j--){rMax=Math.max(rMax-1,dp[j]);t[j]=Math.max(t[j],rMax);}for (int j=0;j<m;j++){t[j]+=points[i][j];}dp=t;}long res=0;for (int j=0;j<m;j++){res= Math.max(res,dp[j]);}return res;}
}