在有向圖中,以某個節點為起始節點,從該點出發,每一步沿著圖中的一條有向邊行走。如果到達的節點是終點(即它沒有連出的有向邊),則停止。
對于一個起始節點,如果從該節點出發,無論每一步選擇沿哪條有向邊行走,最后必然在有限步內到達終點,則將該起始節點稱作是 安全 的。
返回一個由圖中所有安全的起始節點組成的數組作為答案。答案數組中的元素應當按 升序 排列。
該有向圖有 n 個節點,按 0 到 n - 1 編號,其中 n 是?graph?的節點數。圖以下述形式給出:graph[i] 是編號 j 節點的一個列表,滿足 (i, j) 是圖的一條有向邊。
- 示例 1:
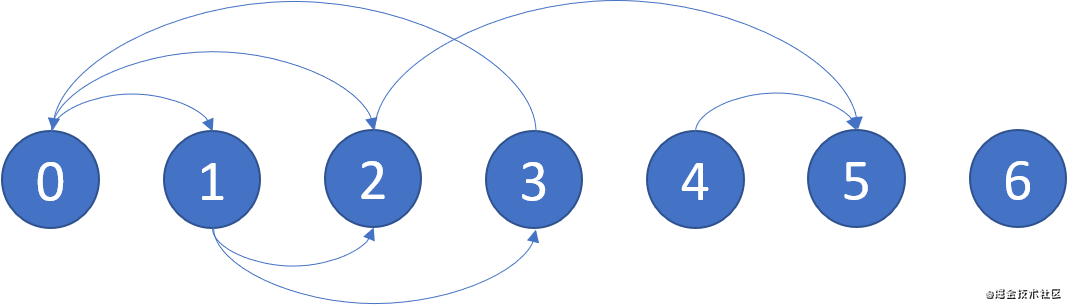
輸入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
輸出:[2,4,5,6]
解釋:示意圖如上。
- 示例 2:
輸入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
輸出:[4]
提示:
n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
graph[i] 按嚴格遞增順序排列。
圖中可能包含自環。
圖中邊的數目在范圍 [1, 4 * 104] 內。
解題思路
這題原來的路徑是從起點經過所以的可能路徑都能到達終點,也就是說我們路徑上不能產生環,我們可以使用拓撲排序來檢查是否有環的產生。
- 我們先將圖的指向全部變為反向,那么我們的目標就變為從終點去到達起點
- map維護一個節點指向其他節點的邊,使用一個數組維護每個節點的入度
- 當節點的入度為0時,代表該節點的依賴節點已經全部滿足,可以將當前節點刪除,將其指向的節點全部入度減去1,而對于環,因為他們的節點之間存在循環的依賴,因此永遠不可能被刪除,所以最后入度為0就是可在有限步內到達終點的節點
代碼
class Solution {public List<Integer> eventualSafeNodes(int[][] graph) {int n = graph.length;Queue<Integer> queue=new LinkedList<>();Map<Integer,List<Integer>> map=new HashMap<>();int[] degree=new int[n];for (int i = 0; i < graph.length; i++) {for (int j : graph[i]) {map.putIfAbsent(j,new ArrayList<Integer>());map.get(j).add(i);}degree[i]=graph[i].length;if (degree[i]==0)queue.add(i);}while (!queue.isEmpty()){Integer cur = queue.poll();for (Integer next : map.getOrDefault(cur, new ArrayList<>())) {if (--degree[next]==0)queue.add(next);}}ArrayList<Integer> res = new ArrayList<>();for (int i = 0; i < n; i++) {if (degree[i]==0)res.add(i);}return res;}
}



















