441. 排列硬幣

你總共有 n 枚硬幣，并計劃將它們按階梯狀排列。對于一個由 k 行組成的階梯，其第 i 行必須正好有 i 枚硬幣。階梯的最后一行 可能 是不完整的。

給你一個數字 n ，計算并返回可形成 完整階梯行 的總行數。

示例 1：

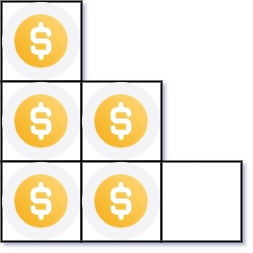
輸入：n = 5
輸出：2
解釋：因為第三行不完整，所以返回 2 。
示例 2：

輸入：n = 8
輸出：3
解釋：因為第四行不完整，所以返回 3 。

解題思路

• 每一行的硬幣數量是一個等差數列，首項為1，公差為1，因此硬幣數量和行數的關系滿足等差數列的求和公式。
• 通過硬幣的行數，我們就可以得知硬幣總數，因此我們可以使用二分查找，找出一個滿足硬幣總數的最大行數

代碼

class Solution {public int arrangeCoins(int n) {if(n==1) return 1;  int l=1,r=n/2+1;while(l<=r){int mid=(r-l)/2+l;if((mid+(long)mid*(mid-1)/2)>n)r=mid-1;else  l=mid+1;}return r;}
}