文章目錄

前言

?1. 樹的概念及結構

? ?1.1 樹的概念

?1.2 樹的基礎概念

1.3 樹的表示

1.4 樹的應用

?2. 二叉樹

2.1 二叉樹的概念

?2.2 二叉樹的遍歷

前言

????????在計算機科學中，數據結構是解決問題的關鍵。而二叉樹作為最基本、最常用的數據結構之一，不僅在算法和數據處理中發揮著重要作用，也在日常生活中有著豐富的應用。無論是搜索引擎的索引算法、文件系統的組織方式，還是編譯器的語法分析，二叉樹都扮演著不可或缺的角色。為了便于大家更好的入門二叉樹，本期先向大家簡單介紹一下二叉樹的基本性質，以及代碼理解實現，給大家預預熱。

?1. 樹的概念及結構

? ?1.1 樹的概念

?????????樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。把它叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。

有一個特殊的結點，稱為根結點，根節點沒有前驅結點
除根節點外，其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm，其中每一個集合Ti(1<= i<= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以有0個或多個后繼
因此，樹是遞歸定義的。

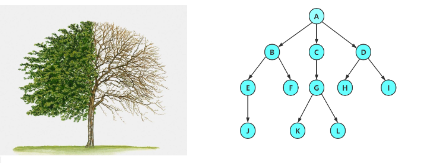
?那這樣是樹還是非樹？

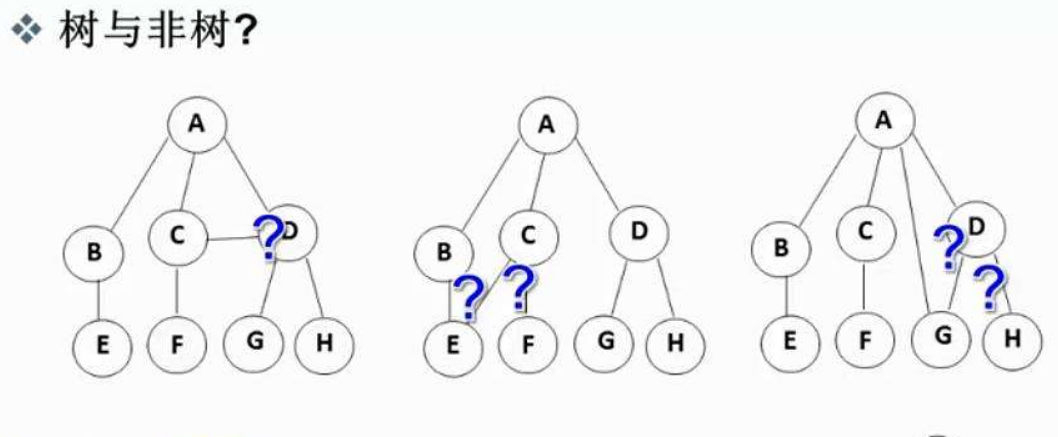
?答案是非樹，樹形結構中，子樹之間不能有交集，否則就不是樹形結構。

?1.2 樹的基礎概念

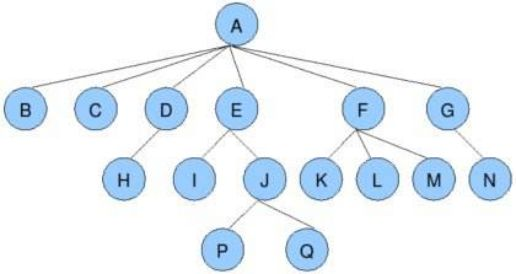
節點的度：一個節點含有的子樹的個數稱為該節點的度；如上圖：A的為6
葉節點或終端節點：度為0的節點稱為葉節點；如上圖：B、C、H、I...等節點為葉節點
*非終端節點或分支節點：度不為0的節點；如上圖：D、E、F、G...等節點為分支節點
雙親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點；如上圖：A是B的父節點
孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點；如上圖：B是A的孩子節點
兄弟節點：具有相同父節點的節點互稱為兄弟節點；如上圖：B、C是兄弟節點
樹的度：一棵樹中，最大的節點的度稱為樹的度；如上圖：樹的度為6
*節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推；
*樹的高度或深度：樹中節點的最大層次；如上圖：樹的高度為4
*堂兄弟節點：雙親在同一層的節點互為堂兄弟；如上圖：H、I互為兄弟節點
*節點的祖先：從根到該節點所經分支上的所有節點；如上圖：A是所有節點的祖先
*子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫
*森林：由m（m>0）棵互不相交的樹的集合稱為森林；

帶星號的了解即可。

????????這里我們重點說一下樹的高度和節點層次，不同的數據結構書中一般有兩種方式表示樹的高度，一種是從0開始例如上述的樹，根節點A高度就是0，到P、Q高度就是3。另外一種是從1開始，根節點1的高度為1，那P、Q的高度就是4。個人更推薦使用從1開始的，如果使用從0開始的，那如果是空樹，在使用0表示就有點說不過去了，那空樹的高度就只能是-1了。如果使用從1開始的，那空樹就可以使用0來表示。

1.3 樹的表示

?????????樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，既然保存值域，也要保存結點和結點之間的關系，實際中樹有很多種表示方式如：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。

? ? ? ? ?首先在定義樹的節點時就很為難，一個節點到底要定義多少個指向子節點的指針：

struct TreeNode
{Datatype x;struct TreeNode* child1;struct TreeNode* child2;……};

?要想定義一個節點就要先知道一個樹的度，例如上述的樹：

?????????這棵樹的度為6，那我們定義時就要定義6個指針變量嗎？那大部分的節點的子節點并沒有達到6個，這樣就會很浪費，定義也很費勁。

在C++中，有這樣一種定義方法：

struct TreeNode
{Datatype x;vector<struct TreeNode*> childs;
};

?????????可以不規定個數，它使用數組的方式來存儲，如果不夠還可以進行增容，這種方式是使用順序表來存儲孩子節點的信息。

?????????還有一種非常巧的方式，叫孩子兄弟表示法，即左孩子右兄弟。

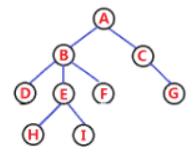
?????????拿這棵樹為例，這種方法在定義節點時就只定義兩個指針，一個指針叫左孩子指針，一個指針叫右兄弟指針。怎么指向呢？就是說無論一個節點有多少個孩子，它的孩子指針就只指向第一個孩子（最左邊的孩子節點），剩下的孩子用第一個孩子的兄弟指針指向第二個，第二個孩子的兄弟指針指向第三個。

表示出來就是這樣的結構：

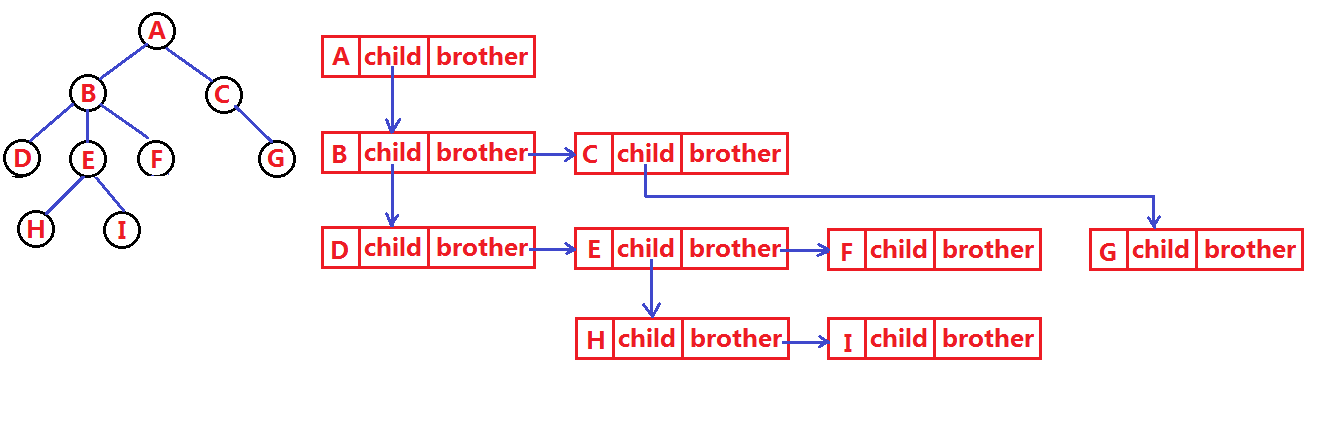?除此之外還有其他的表示法，這里就不再一一列舉。

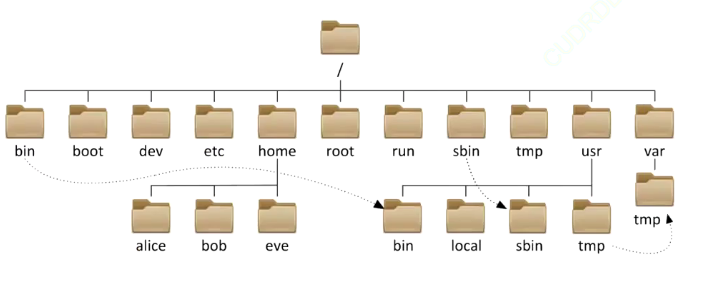
1.4 樹的應用

?在現實生活中我們也經常使用到樹狀結構，例如：文件存儲

?2. 二叉樹

?? ? ? ? 了解完樹的基本概念后，我們接下來進入二叉樹的學習。

2.1 二叉樹的概念

?一棵二叉樹是結點的一個有限集合，該集合:

或者為空
由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成

?二叉樹的特點：

二叉樹不存在度大于2的結點
二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹

?對于任何一顆二叉樹都是由一下幾種情況復合而成。

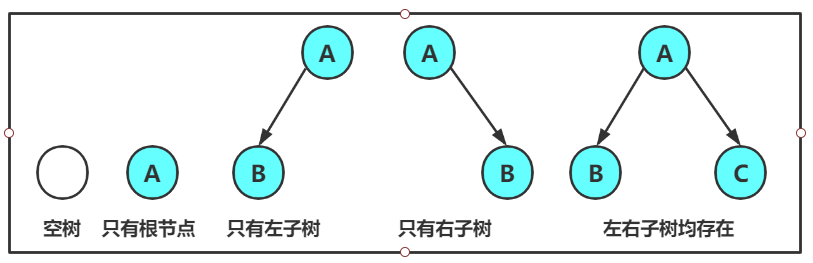
?????????當然關于二叉樹的基礎概念還有很多，今天就先簡單介紹，接下來給大家來點干貨，先讓大家切身體驗一下二叉樹。? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

?2.2 二叉樹的遍歷

?當我們看到任何一顆二叉樹都應該把它分為三個部分：

根節點
左子樹
右子樹

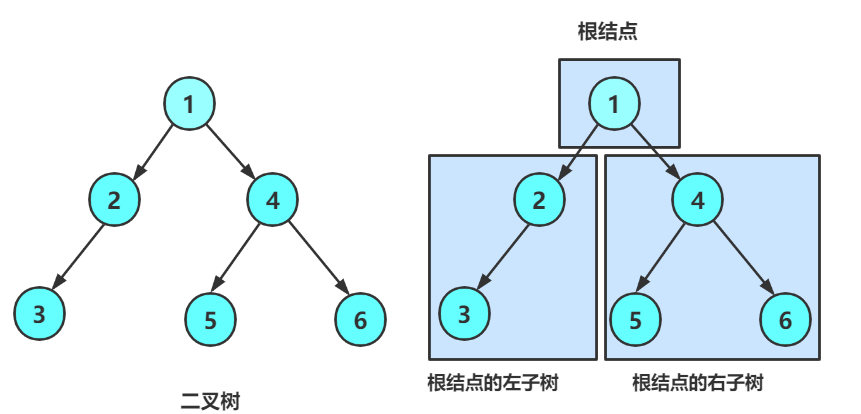
?我們以這棵樹為例進行分析：

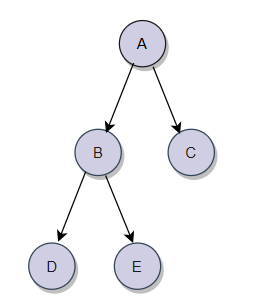
?????????A為這棵樹的根節點，B及其以下的節點（D、E）被稱為左子樹，C及其以下節點被稱為右子樹。然后B子樹仍然可以分為D及其以下節點是左子樹，E及其以下節點是右子樹，然后再分，直到子節點為NULL，停止。

我們這里用的是分治算法。分治算法：

????????把大問題分成類似的子問題，子問題再分成子問題，……，直到子問題無法再分割為止。

遍歷可分為三種：

前序：也叫先根遍歷，遍歷順序為：根、左子樹、右子樹

中序：也叫中根遍歷，遍歷順序為：左子樹、根、右子樹

后序：也叫后根遍歷，遍歷順序為：左子樹、右子樹、根

?????????我們先來嘗試以下前序遍歷，理解了前序遍歷后兩個就簡單了。還是以這棵樹為例：

?????????前序遍歷，我們是先訪問根，然后是左子樹、右子樹。那應該先遍歷A，然后遍歷A的左子樹B（及其以下節點），然后就以B為根繼續遍歷它的左子樹D（及其以下節點），然后再次以D為根開始，遍歷左子樹（NULL），然后開始返回到D，D再遍歷右子樹（NULL），然后D（這個子樹）就遍歷完畢，返回到B，B開始遍歷右子樹E（及其以下節點），E左子樹為NULL返回到E，然后遍歷右子樹，右子樹也為空（E子樹遍歷完畢），然后返回E（B的右子樹遍歷完畢），接著返回B（B的所有子樹遍歷完畢），接著返回到A，A開始遍歷右子樹……這個規律很符合遞歸。

????????遍歷完的順序為：A、B、D、NULL、NULL、E、NULL、NULL、C、NULL、NULL。大部分學校講的都是A、B、D、E、C。大部分同學應該都知道這個規律，但不知道為什么這樣遍歷。

????????根據這個思路我們再來寫一下中序遍歷，中序遍歷先訪問左子樹，然后是跟，最后是右子樹。還是從A開始找，A的左子樹B，然后以B為根，找B的左子樹，接著以D為根，找D的左子樹，D的左子樹為NULL（D左子樹遍歷結束），返回到D（根），開始遍歷D的右子樹……

?????????最后遍歷的順序為：【NULL、D、NULL(B的左子樹）、B(根)、NULL、E、NULL? ? ? ? ? ? ? (B的右子樹）、】(A的左子樹）、A(根）、【NULL、C、NULL】(A的右子樹）。整理一下：

NULL、D、NULL、B、NULL、E、NULL、A、NULL、C、NULL（D、B、E、C、A）。

? ? ? ? ?我們接著寫一下后序遍歷：NULL、NULL、D、NULL、NULL、E、B、NULL、NULL、C、A（D、E、B、C、A）。

我們再來練一個：

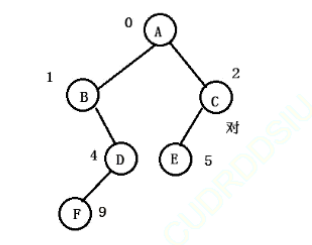
?????????前序遍歷：A（根）||這部分為整體二叉樹的根、B（左子樹）、NULL（B的左子樹）、D（B的右子樹）、F（D的左子樹）、NULL（F的左子樹）、NULL（F的右子樹）、NULL（D的右子樹）||這部分屬于A的左子樹、C、E、NULL（E的左子樹）、NULL（E的右子樹）、NULL（C的右子樹）||這部分為A的右子樹。

?后續的中序遍歷和后續遍歷大家可以自己私下練一下。

????????好了我們已經了解了遍歷，接下來我們來說實現以下前序遍歷。給大家來點干貨，便于大家更好理解。

?我們依然以這個簡單的二叉樹為例進行實現。

?我們先定義一個二叉樹的節點：

typedef char Datatype;
typedef struct BinaryTreeNode
{Datatype data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

?然后就是它的前序遍歷的實現：

void PrevOrder(BTNode* root)
{}

????????我們知道前序遍歷的順序是根，然后是左子樹，最后是右子樹。因此在開始前我們先判斷以下root是否為NULL，如果不為NULL我們就打印根節點的數據。?

void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);}

?????????那如何遍歷到左子樹、右子樹呢？其實很簡單，我們之前介紹的時候說：二叉樹的遍歷復合遞歸結構，這里我們就可以使用遞歸來完成遍歷，代碼如下：

void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

?????????先遍歷左子樹，再遍歷右子樹，那調用的順序就先調用自己傳左孩子指針過去，以左孩子節點為根，再按照這個程序進行執行，再次傳左孩子指針過去……，知道左孩子為NULL，返回上一層，開始遍歷右子樹。

?我們可以簡單粗暴的測試以下，測試代碼如下：

#include<stdio.h>
#include<stdlib.h>typedef char Datatype;
typedef struct BinaryTreeNode
{Datatype data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;PrevOrder(A);printf("\n");return 0;
}

執行結果：

?和上述分析的結果一致。

那剩下的中序遍歷和后序遍歷也很簡單，只需要改變一下遞歸調用函數的次序即可：

//中序遍歷
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}//后序遍歷
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);}

?我們也可以測試以下看看執行結果，測試代碼如下：

typedef struct BinaryTreeNode
{Datatype data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);}
int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;printf("前序遍歷：");PrevOrder(A);printf("\n");printf("中序遍歷：");InOrder(A);printf("\n");printf("后序遍歷：");PostOrder(A);printf("\n");return 0;
}

?執行結果如下：

?可以和上邊的分析對比一下，沒有問題，

總結

????????二叉樹遍歷是學習和理解二叉樹的重要部分。通過遍歷，我們可以按照特定的順序訪問二叉樹的節點，從而深入了解它們的結構和關系。在這篇博客中，我們介紹了三種常見的二叉樹遍歷方式：前序遍歷、中序遍歷和后序遍歷，并對它們的原理、特點和應用進行了詳細討論。本期內容為預熱階段，先讓大家熟悉一下二叉樹，以便于后續二叉樹的學習，好的本期內容到此結束，感謝閱讀！