I recently came across the article titled High-dimensional data clustering by using local affine/convex hulls by HakanCevikalp in Pattern Recognition Letters. It proposes a novel algorithm to cluster high-dimensional data using local affine/convex hulls. I was inspired by their method of using convex hulls for clustering. I wanted to give a try at implementing my own simple clustering approach using convex hulls. So, in this article, I will walk you through my implementation of my clustering approach using convex hulls. Before we get into coding, let’s see what a convex hull is.

我最近在“ 模式識別字母”中碰到了一篇文章，標題為HakanCevikalp 使用本地仿射/凸包來進行高維數據聚類 。 提出了一種使用局部仿射/凸包對高維數據進行聚類的新算法。 他們使用凸包進行聚類的方法給我啟發。 我想嘗試使用凸包實現我自己的簡單聚類方法。 因此，在本文中，我將引導您完成使用凸包的聚類方法的實現。 在進行編碼之前，讓我們看看什么是凸包。

凸包 (Convex Hull)

According to Wikipedia, a convex hull is defined as follows.

根據維基百科 ，凸包的定義如下。

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it.

在幾何中，形狀的凸包或凸包絡或凸包是包含該形狀的最小凸集。

Let us consider an example of a simple analogy. Assume that there are a few nails hammered half-way into a plank of wood as shown in Figure 1. You take a rubber band, stretch it to enclose the nails and let it go. It will fit around the outermost nails (shown in blue) and take a shape that minimizes its length. The area enclosed by the rubber band is called the convex hull of the set of nails.

讓我們考慮一個簡單類比的例子。 如圖1所示，假設有一些釘子被釘在一塊木板上。將橡皮筋拉開，將其拉緊以包住釘子，然后松開。 它將適合最外面的釘子(以藍色顯示)，并具有使長度最小化的形狀。 橡皮筋包圍的區域稱為釘組的凸包 。

This convex hull (shown in Figure 1) in 2-dimensional space will be a convex polygon where all its interior angles are less than 180°. If it is in a 3-dimensional or higher-dimensional space, the convex hull will be a polyhedron.

這個在二維空間中的凸包(如圖1所示)將是一個凸多邊形 ，其所有內角均小于180°。 如果在3維或更高維空間中，則凸包將是多面體 。

There are several algorithms that can determine the convex hull of a given set of points. Some famous algorithms are the gift wrapping algorithm and the Graham scan algorithm.

有幾種算法可以確定給定點集的凸包。 一些著名的算法是禮品包裝算法和Graham掃描算法 。

Since a convex hull encloses a set of points, it can act as a cluster boundary, allowing us to determine points within a cluster. Hence, we can make use of convex hulls and perform clustering. Let’s get into the code.

由于凸包包圍著一組點，因此它可以充當群集邊界，從而使我們能夠確定群集中的點。 因此，我們可以利用凸包并執行聚類。 讓我們進入代碼。

一個簡單的例子 (A Simple Example)

I will be using Python for this example. Before getting started, we need the following Python libraries.

我將在此示例中使用Python。 在開始之前，我們需要以下Python庫。

sklearn
numpy
matplotlib
mpl_toolkits
itertools
scipy
quadprog

數據集 (Dataset)

To create our sample dataset, I will be using sci-kit learn library’s make blobs function. I will make 3 clusters.

為了創建示例數據集，我將使用sci-kit學習庫的make blobs函數。 我將制作3個群集。

import numpy as np
from sklearn.datasets import make_blobscenters = [[0, 1, 0], [1.5, 1.5, 1], [1, 1, 1]]
stds = [0.13, 0.12, 0.12]X, labels_true = make_blobs(n_samples=1000, centers=centers, cluster_std=stds, random_state=0)
point_indices = np.arange(1000)

Since this is a dataset of points with 3 dimensions, I will be drawing a 3D plot to show our ground truth clusters. Figure 2 denotes the scatter plot of the dataset with coloured clusters.

由于這是3維點的數據集，因此我將繪制3D圖以顯示我們的地面真相群集。 圖2表示帶有彩色簇的數據集的散點圖。

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Dx = X[:,0]
y = X[:,1] 
z = X[:,2]
# Creating figure 
fig = plt.figure(figsize = (15, 10)) 
ax = plt.axes(projection ="3d") 
    
# Add gridlines  
ax.grid(b = True, color ='grey',  
        linestyle ='-.', linewidth = 0.3,  
        alpha = 0.2)  
  
mycolours = ["red", "green", "blue"]# Creating color map 
col = [mycolours[i] for i in labels_true]# Creating plot 
sctt = ax.scatter3D(x, y, z, c = col, marker ='o')plt.title("3D scatter plot of the data\n") 
ax.set_xlabel('X-axis', fontweight ='bold')  
ax.set_ylabel('Y-axis', fontweight ='bold')  
ax.set_zlabel('Z-axis', fontweight ='bold')
  
# show plot 
plt.draw()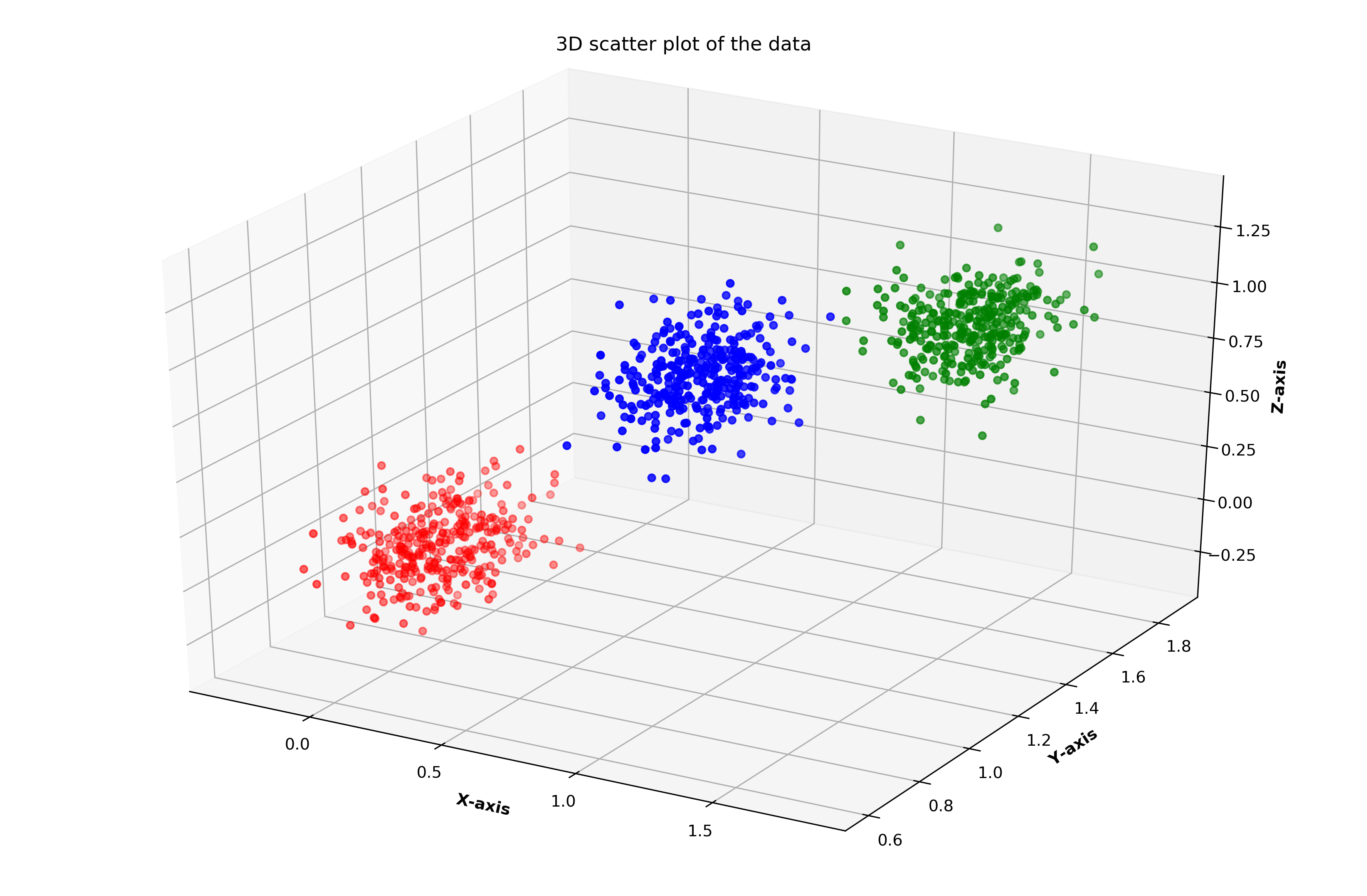

獲取初始聚類 (Obtaining an Initial Clustering)

First, we need to break our dataset into 2 parts. One part will be used as seeds to obtain an initial clustering using K-means. The points in the other part will be assigned to clusters based on the initial clustering.

首先，我們需要將數據集分為兩部分。 一部分將用作種子，以使用K均值獲得初始聚類。 另一部分中的點將根據初始聚類分配給聚類。

from sklearn.model_selection import train_test_splitX_seeds, X_rest, y_seeds, y_rest, id_seeds, id_rest = train_test_split(X, labels_true, point_indices, test_size=0.33, random_state=42)

Now we perform K-means clustering on the seed points.

現在我們對種子點執行K-均值聚類。

from sklearn.cluster import KMeanskmeans = KMeans(n_clusters=3, random_state=9).fit(X_seeds)
initial_result = kmeans.labels_

Since the resulting labels may not be the same as the ground truth labels, we have to map the two sets of labels. For this, we can use the following function.

由于生成的標簽可能與地面真相標簽不同，因此我們必須映射兩組標簽。 為此，我們可以使用以下功能。

from itertools import permutations# Source: https://stackoverflow.com/questions/11683785/how-can-i-match-up-cluster-labels-to-my-ground-truth-labels-in-matlabdef remap_labels(pred_labels, true_labels):    pred_labels, true_labels = np.array(pred_labels), np.array(true_labels)
    assert pred_labels.ndim == 1 == true_labels.ndim
    assert len(pred_labels) == len(true_labels)
    cluster_names = np.unique(pred_labels)
    accuracy = 0    perms = np.array(list(permutations(np.unique(true_labels))))    remapped_labels = true_labels    for perm in perms:        flipped_labels = np.zeros(len(true_labels))
        for label_index, label in enumerate(cluster_names):
            flipped_labels[pred_labels == label] = perm[label_index]        testAcc = np.sum(flipped_labels == true_labels) / len(true_labels)        if testAcc > accuracy:
            accuracy = testAcc
            remapped_labels = flipped_labels    return accuracy, remapped_labels

We can get the accuracy and the mapped initial labels from the above function.

我們可以從上面的函數中獲得準確性和映射的初始標簽。

intial_accuracy, remapped_initial_result = remap_labels(initial_result, y_seeds)

Figure 3 denotes the initial clustering of the seed points.

圖3表示種子點的初始聚類。

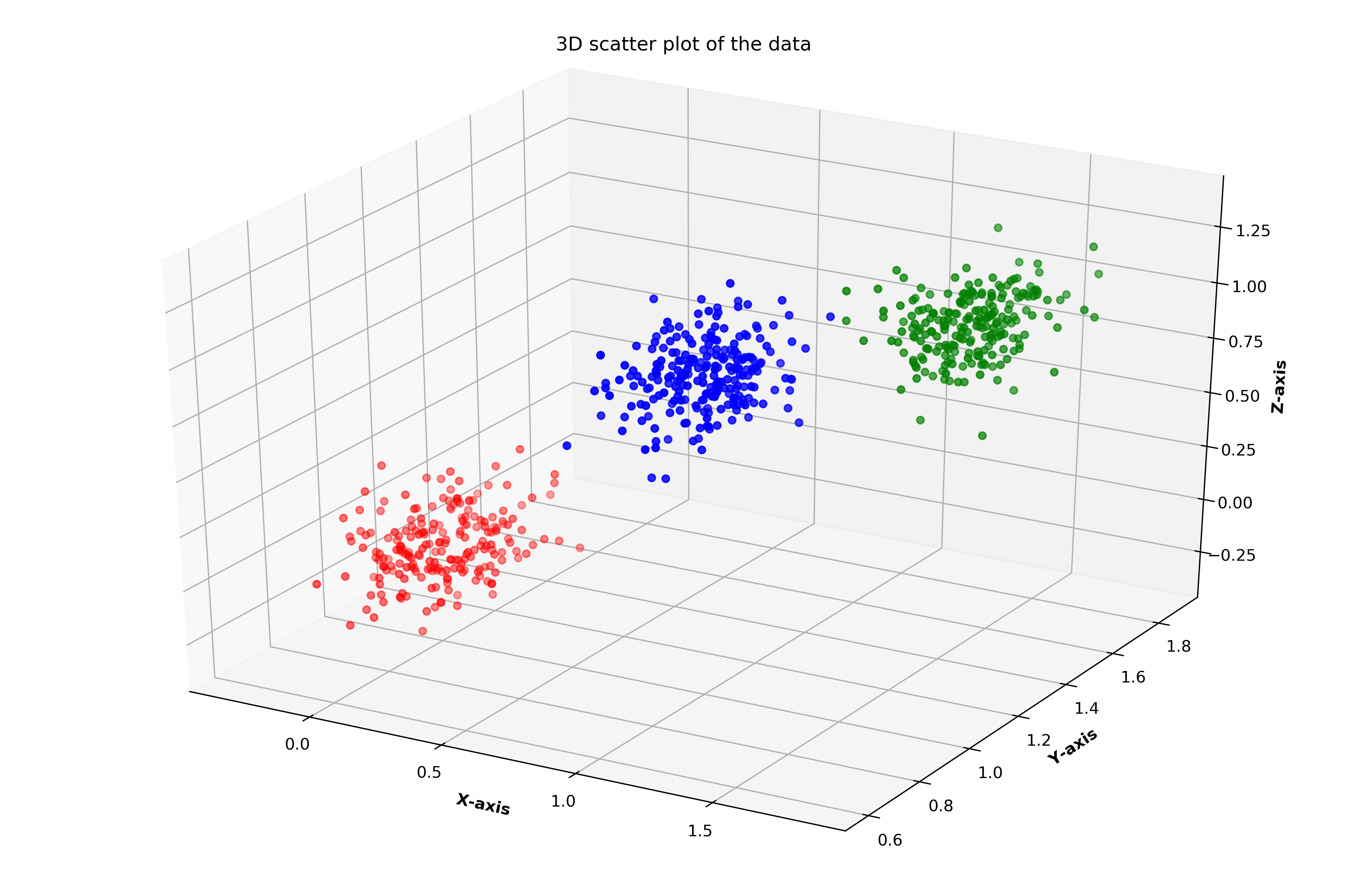
獲取初始聚類的凸包 (Get Convex Hulls of the Initial Clustering)

Once we have obtained an initial clustering, we can get the convex hulls for each cluster. First, we have to get the indices of each data point in the clusters.

一旦獲得初始聚類，就可以獲取每個聚類的凸包。 首先，我們必須獲取群集中每個數據點的索引。

# Get the idices of the data points belonging to each cluster
indices = {}for i in range(len(id_seeds)):
    if int(remapped_initial_result[i]) not in indices:
        indices[int(remapped_initial_result[i])] = [i]
    else:
        indices[int(remapped_initial_result[i])].append(i)

Now we can obtain the convex hulls from each cluster.

現在我們可以從每個聚類中獲得凸包。

from scipy.spatial import ConvexHull# Get convex hulls for each cluster
hulls = {}for i in indices:
    hull = ConvexHull(X_seeds[indices[i]])
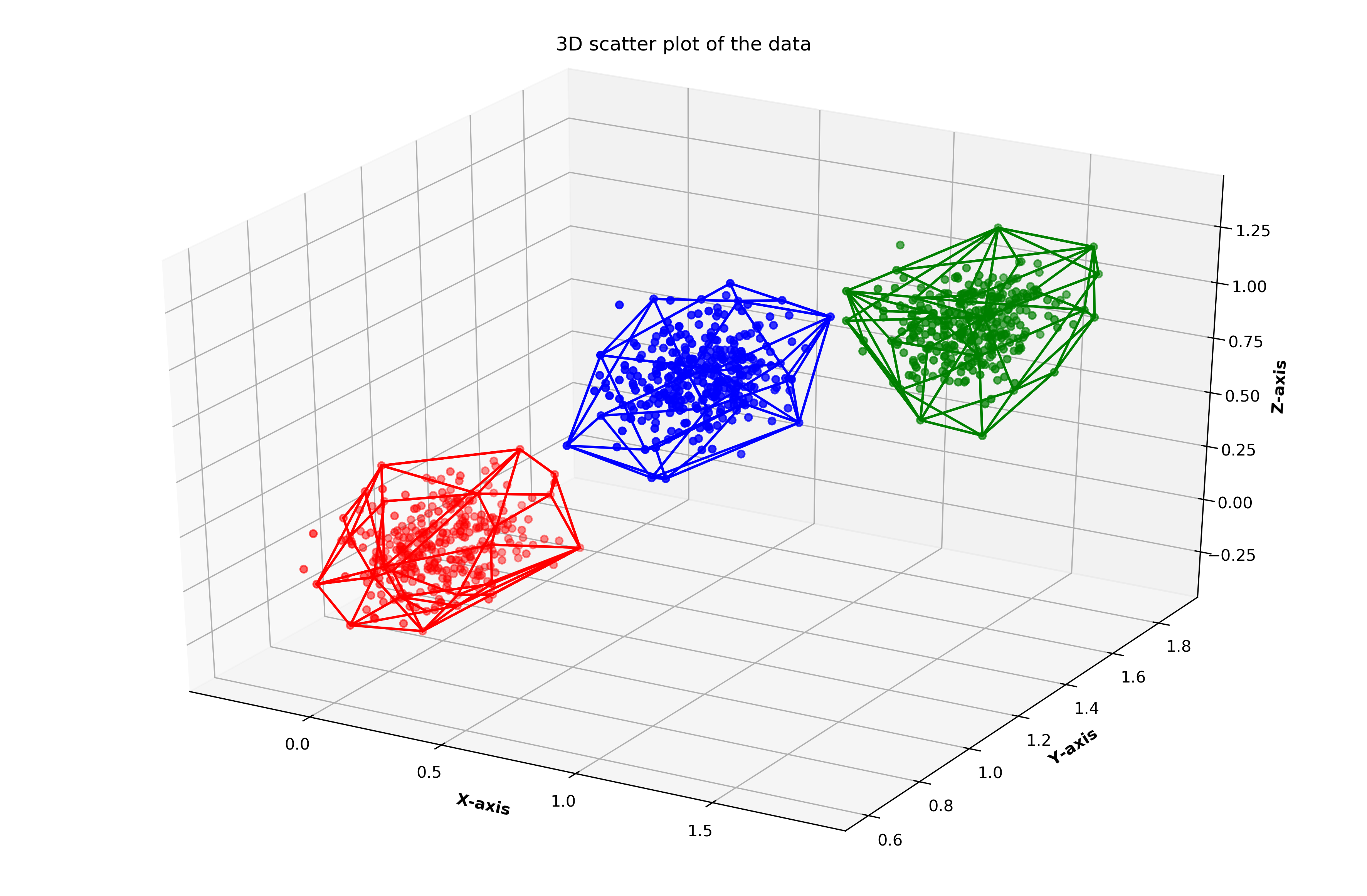
    hulls[i] = hull

Figure 4 denotes the convex hulls representing each of the 3 clusters.

圖4表示分別代表3個群集的凸包。

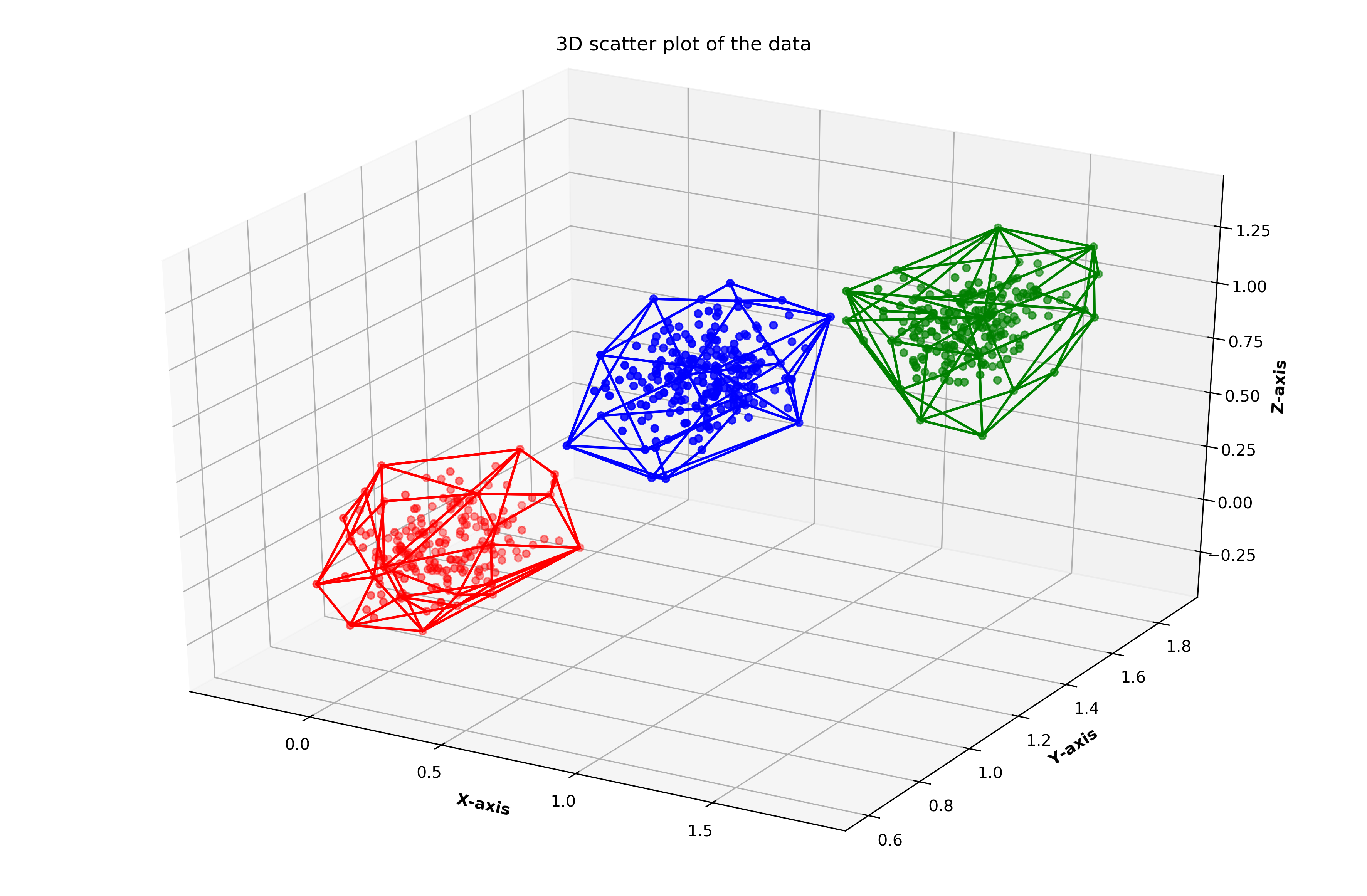
將剩余點分配給最接近的凸包的群集 (Assign Remaining Points to the Cluster of the Closest Convex Hull)

Now that we have the convex hulls of the initial clusters, we can assign the remaining points to the cluster of the closest convex hull. First, we have to get the projection of the data point on to a convex hull. To do so, we can use the following function.

現在我們有了初始聚類的凸包，我們可以將其余點分配給最接近的凸包的聚類。 首先，我們必須將數據點投影到凸包上。 為此，我們可以使用以下功能。

from quadprog import solve_qp# Source: https://stackoverflow.com/questions/42248202/find-the-projection-of-a-point-on-the-convex-hull-with-scipydef proj2hull(z, equations):    G = np.eye(len(z), dtype=float)
    a = np.array(z, dtype=float)
    C = np.array(-equations[:, :-1], dtype=float)
    b = np.array(equations[:, -1], dtype=float)    x, f, xu, itr, lag, act = solve_qp(G, a, C.T, b, meq=0, factorized=True)    return x

The problem of finding the projection of a point on a convex hull can be solved using quadratic programming. The above function makes use of the quadprog module. You can install the quadprog module using conda or pip.

查找點在凸包上的投影的問題可以使用二次編程解決。 上面的功能利用了quadprog模塊。 您可以安裝quadprog使用模塊conda或pip 。

conda install -c omnia quadprog
OR
pip install quadprog

I won’t go into details about how to solve this problem using quadratic programming. If you are interested, you can read more from here and here.

我不會詳細介紹如何使用二次編程解決此問題。 如果您有興趣，可以從這里和這里內容。

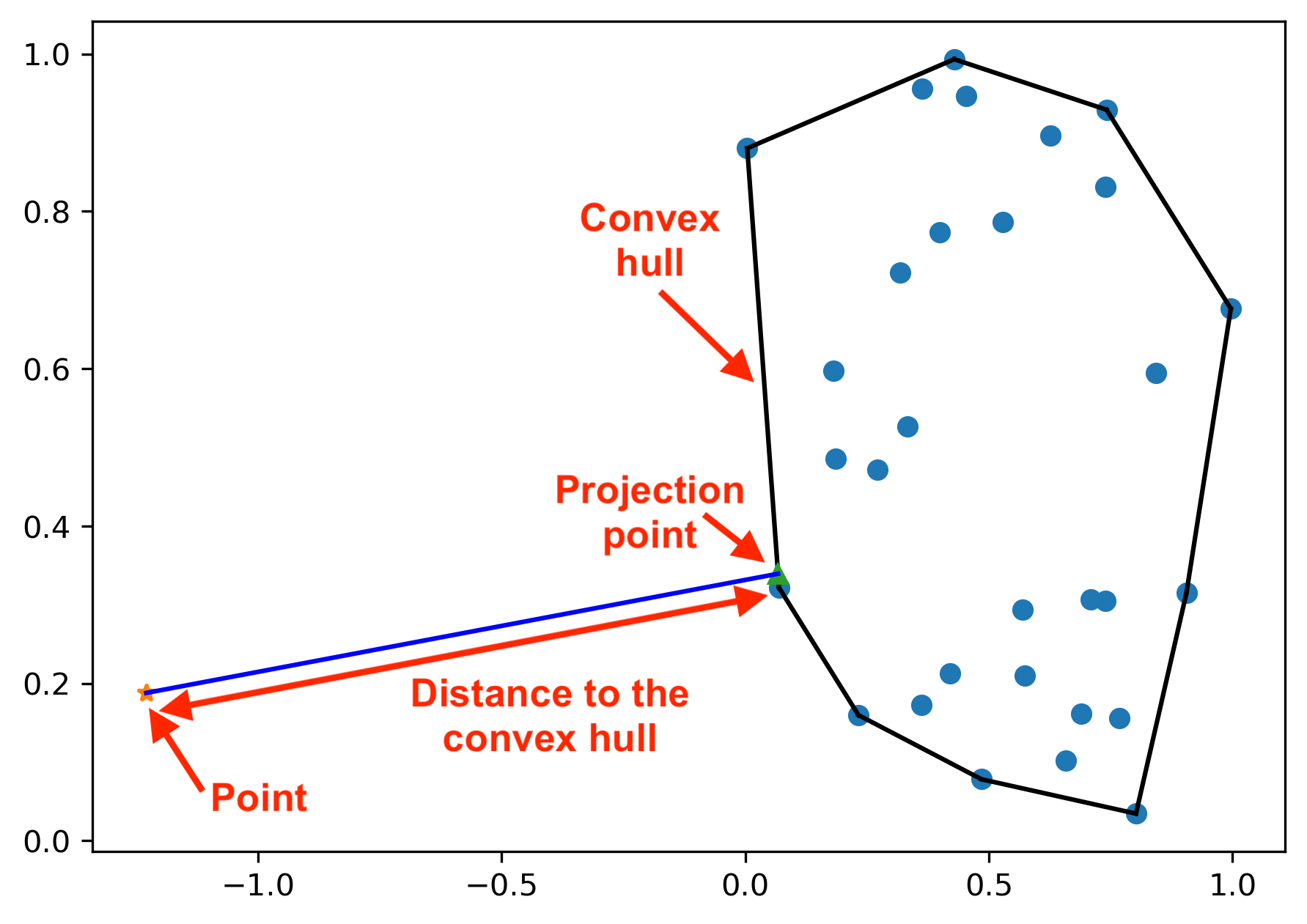
Once you have obtained the projection on the convex hull, you can calculate the distance from the point to the convex hull as shown in Figure 5. Based on this distance, now let’s assign the remaining data points to the cluster of the closest convex hull.

一旦獲得了凸包的投影，就可以計算從點到凸包的距離，如圖5所示。現在，基于該距離，我們將剩余的數據點分配給最近的凸包的群集。

I will consider the Euclidean distance from the data point to its projection on the convex hull. Then the data point will be assigned to the cluster with the convex hull having the shortest distance from that data point. If a point lies within the convex hull, then the distance will be 0.

我將考慮從數據點到其在凸包上的投影的歐幾里得距離。 然后，將數據點分配給群集，其中凸包距該數據點的距離最短。 如果點位于凸包內，則距離將為0。

prediction = []for z1 in X_rest:    min_cluster_distance = 100000
    min_distance_point = ""
    min_cluster_distance_hull = ""
    
    for i in indices:        p = proj2hull(z1, hulls[i].equations)        dist = np.linalg.norm(z1-p)        if dist < min_cluster_distance:            min_cluster_distance = dist
            min_distance_point = p
            min_cluster_distance_hull = i    prediction.append(min_cluster_distance_hull)prediction = np.array(prediction)

Figure 6 denotes the final clustering result.

圖6表示最終的聚類結果。

評估最終結果 (Evaluate the Final Result)

Let’s evaluate our result to see how accurate it is.

讓我們評估我們的結果以查看其準確性。

from sklearn.metrics import accuracy_scoreY_pred = np.concatenate((remapped_initial_result, prediction))
Y_real = np.concatenate((y_seeds, y_rest))
print(accuracy_score(Y_real, Y_pred))

I got an accuracy of 1.0 (100%)! Awesome and exciting right? 😊

我的準確度是1.0(100％)！ 太棒了，令人興奮吧？ 😊

If you want to know more about evaluating clustering results, you can check out my previous article Evaluating Clustering Results.

如果您想了解有關評估聚類結果的更多信息，可以查閱我之前的文章評估聚類結果 。

I have used a very simple dataset. You can try this method with more complex datasets and see what happens.

我使用了一個非常簡單的數據集。 您可以對更復雜的數據集嘗試此方法，然后看看會發生什么。

高維數據 (High-dimensional data)

I also tried to cluster a dataset with data points having 8 dimensions using my cluster hull method. You can find the jupyter notebook showing the code and results. The final results are as follows.

我還嘗試使用我的群集包方法將數據集與8個維度的數據點群集在一起。 您可以找到顯示代碼和結果的jupyter筆記本 。 最終結果如下。

Accuracy of K-means method: 0.866
Accuracy of Convex Hull method: 0.867

There is a slight improvement in my convex hull method over K-means.

與K均值相比，我的凸包方法略有改進。

最后的想法 (Final Thoughts)

The article titled High-dimensional data clustering by using local affine/convex hulls by HakanCevikalp shows that the convex hull-based method they proposed avoids the “hole artefacts” problem (the sparse and irregular distributions in high-dimensional spaces can make the nearest-neighbour distances unreliable) and improves the accuracy of high-dimensional datasets over other state-of-the-art subspace clustering methods.

由HakanCevikalp撰寫的使用局部仿射/凸包進行高維數據聚類的文章顯示，他們提出的基于凸包的方法避免了“ Kong偽像 ”問題(高維空間中稀疏和不規則的分布可以使最近的鄰居距離不可靠)，并比其他最新的子空間聚類方法提高了高維數據集的準確性。

You can find the jupyter notebook containing the code used for this article.

您可以找到包含本文所用代碼的jupyter筆記本 。

Hope this article was interesting and useful.

希望本文有趣而有用。

Cheers! 😃

干杯! 😃