目錄

特征預處理

1、簡述

2、內容

3、歸一化

3.1、魯棒性

3.2、存在的問題

4、標準化

---

?所屬專欄：人工智能

文中提到的代碼如有需要可以私信我發給你😊

特征預處理

1、簡述

什么是特征預處理：scikit-learn的解釋：

provides several common utility functions and transformer classes to change raw feature vectors into a representation that is more suitable for the downstream estimators.

翻譯過來：通過一些轉換函數將特征數據轉換成更加適合算法模型的特征數據過程

詳述：

特征預處理是機器學習和數據分析中的一個重要步驟，它旨在將原始數據轉換為適合機器學習算法的形式，以提高模型的性能和穩定性。特征預處理涵蓋了一系列數據轉換和處理操作，用于清洗、歸一化、縮放、編碼等，以確保輸入特征的質量和一致性。以下是特征預處理的一些常見操作和方法：

1. 數據清洗和處理：處理缺失值、異常值和噪聲，確保數據的完整性和準確性。常見的方法包括填充缺失值、平滑噪聲、剔除異常值等。
2. 特征縮放：將不同尺度的特征縮放到相似的范圍，以避免某些特征對模型的影響過大。常見的特征縮放方法有標準化（Z-score標準化）和歸一化（Min-Max縮放）。
3. 特征選擇：選擇對目標變量有重要影響的特征，減少維度和噪聲，提高模型的泛化能力。常見的特征選擇方法有基于統計指標的方法（如方差選擇、卡方檢驗）、基于模型的方法（如遞歸特征消除）、以及基于嵌入式方法（如L1正則化）。
4. 特征轉換：將原始特征轉換為更適合模型的形式，如多項式特征、交叉特征、主成分分析（PCA）等。這可以幫助模型更好地捕捉數據的模式和結構。
5. 特征編碼：將非數值型的特征轉換為數值型的形式，以便機器學習算法處理。常見的編碼方法有獨熱編碼（One-Hot Encoding）和標簽編碼（Label Encoding）。
6. 文本特征提取：將文本數據轉換為數值特征表示，如詞袋模型、TF-IDF特征提取等，以便用于文本分析和機器學習。
7. 特征組合和交叉：將多個特征進行組合或交叉，創建新的特征以捕捉更多的信息。這有助于挖掘特征之間的相互作用。
8. 數據平衡處理：在處理不平衡數據集時，可以使用欠采樣、過采樣等方法來平衡正負樣本的數量，以避免模型偏向于多數類。

特征預處理的目標是使數據更適合機器學習模型，提高模型的性能和穩定性，并且能夠更好地捕捉數據的特征和模式。正確的特征預處理可以顯著影響機器學習模型的結果和效果。不同的數據類型和問題可能需要不同的特征預處理方法，因此在進行特征預處理時需要根據具體情況進行選擇和調整。

2、內容

包含內容：數值型數據的無量綱化：歸一化、標準化 (二者放在后面詳述)

什么是無量綱化：

無量綱化（Dimensionality Reduction）是特征工程的一部分，指的是將數據特征轉換為合適的尺度或形式，以便更好地適應機器學習算法的要求。無量綱化的目的是減少特征的維度，同時保留數據中的重要信息，從而降低計算成本、避免維度災難，并提高模型的性能和泛化能力。

無量綱化可以分為兩種常見的方法：

①特征縮放（Feature Scaling）：特征縮放是將特征的數值范圍調整到相似的尺度，以便機器學習算法更好地工作。特征縮放的常見方法包括歸一化和標準化。

????????歸一化（Min-Max Scaling）：將特征縮放到一個特定的范圍，通常是[0, 1]。

????????標準化（Z-score Scaling）：將特征縮放為均值為0，標準差為1的分布。

②降維（Dimensionality Reduction）：降維是將高維特征空間映射到低維空間，以減少特征數量并去除冗余信息，從而提高計算效率和模型性能。常見的降維方法包括主成分分析（PCA）和線性判別分析（LDA）等。

????????主成分分析（PCA）：通過線性變換將原始特征投影到新的坐標軸上，使得投影后的數據具有最大的方差。這些新坐標軸稱為主成分，可以按照方差的大小選擇保留的主成分數量，從而降低數據的維度。

????????線性判別分析（LDA）：在降維的同時，盡可能地保留類別之間的區分性信息，適用于分類問題。

無量綱化可以幫助解決特征維度不一致、尺度不同等問題，使得機器學習算法能夠更準確地學習數據的模式和結構。選擇適當的無量綱化方法取決于數據的特點、問題的要求以及模型的性能。

特征預處理使用的API：sklearn.preprocessing

為什么我們要進行歸一化/標準化？

特征的單位或者大小相差較大，或者某特征的方差相比其他的特征要大出幾個數量級，容易影響（支配）目標結果，使得一些算法無法學習到其它的特征

3、歸一化

定義：通過對原始數據進行變換把數據映射到(默認為[0,1])之間

公式：

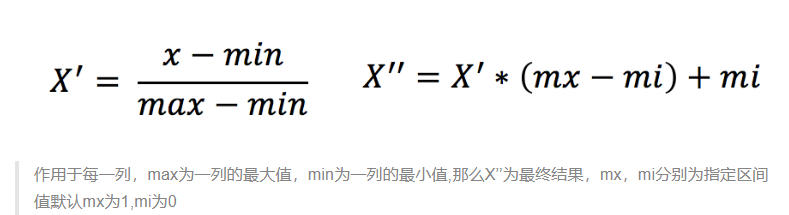
API：

sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )

MinMaxScalar.fit_transform(X)

X:numpy array格式的數據[n_samples,n_features]

返回值：轉換后的形狀相同的array

下面分析會用到一組數據，名為dating.txt。展現如下：

實現：

關鍵代碼解讀：
? ? transfer = MinMaxScaler(feature_range=(2, 3))：
? ? ? ? 實例化一個MinMaxScaler轉換器對象，其中feature_range=(2, 3)表示將數據縮放到范圍為[2, 3]之間。
? ? data = transfer.fit_transform(data[['milage', 'Liters', 'Consumtime']])：
? ? ? ? 使用fit_transform方法將選定的特征（'milage', 'Liters', 'Consumtime'）進行最小-最大歸一化處理。
? ? ? ? fit_transform方法首先計算出特征的最小值和最大值，然后將數據進行線性縮放，使其在指定的范圍內。

# -*- coding: utf-8 -*-
# @Author:︶ㄣ釋然
# @Time: 2023/8/15 21:52
import pandas as pd
from sklearn.preprocessing import MinMaxScaler  # 最大最小值歸一化轉換器'''
歸一化處理。
關鍵代碼解讀：transfer = MinMaxScaler(feature_range=(2, 3))：實例化一個MinMaxScaler轉換器對象，其中feature_range=(2, 3)表示將數據縮放到范圍為[2, 3]之間。data = transfer.fit_transform(data[['milage', 'Liters', 'Consumtime']])：使用fit_transform方法將選定的特征（'milage', 'Liters', 'Consumtime'）進行最小-最大歸一化處理。fit_transform方法首先計算出特征的最小值和最大值，然后將數據進行線性縮放，使其在指定的范圍內。
'''
def min_max_demo():"""歸一化演示"""data = pd.read_csv("data/dating.txt",delimiter="\t")print(data)# 1、實例化一個轉換器類transfer = MinMaxScaler(feature_range=(2, 3))# 2、調用fit_transformdata = transfer.fit_transform(data[['milage', 'Liters', 'Consumtime']])print("最小值最大值歸一化處理的結果：\n", data)if __name__ == '__main__':min_max_demo()

打印結果：

手動計算(取前9行數據)：

計算坐標為(0,0)的元素，總的計算流程為：[（40920-14488）/（75136-14488）] * （3-2）+2 = 2.435826408≈2.43582641

該結果與程序吻合！！

3.1、魯棒性

魯棒性（Robustness）是指在面對異常值、噪聲和其他不完美情況時，系統能夠繼續正常工作并保持良好性能的能力。在數據分析、統計學和機器學習中，魯棒性是一個重要的概念，指的是算法或方法對異常值和數據擾動的敏感程度。一個魯棒性強的方法在存在異常值或數據變動時能夠保持穩定的性能，而魯棒性較差的方法可能會對異常值產生過度敏感的響應。

在數據處理和分析中，魯棒性的重要性體現在以下幾個方面：

1. 異常值處理：魯棒性的方法能夠有效地識別和處理異常值，而不會因為異常值的存在導致結果的嚴重偏差。
2. 模型訓練：在機器學習中，使用魯棒性的算法可以減少異常值對模型訓練的影響，防止過擬合，并提高模型的泛化能力。
3. 特征工程：在特征工程過程中，選擇魯棒性的特征提取方法可以確保提取的特征對異常值不敏感。
4. 統計分析：魯棒性的統計方法能夠減少異常值對統計分析結果的影響，使得分析結果更可靠。

一些常見的魯棒性方法包括：

• 中位數（Median）：在數據中，中位數對異常值的影響較小，相對于平均值具有更強的魯棒性。
• 百分位數（Percentiles）：百分位數可以幫助識別數據分布的位置和離散程度，對異常值的影響較小。
• Z-score標準化：Z-score標準化將數據轉化為均值為0、標準差為1的分布，能夠對抗異常值的影響。
• IQR（四分位距）方法：使用四分位距來定義異常值的界限，對極端值具有一定的容忍度。
• 魯棒性回歸：使用魯棒性回歸方法可以減少異常值對回歸模型的影響。

總之，魯棒性是數據分析和機器學習中一個重要的考慮因素，能夠保證在現實世界中面對多樣性和不確定性時，方法和模型仍能保持有效性和穩定性。

3.2、存在的問題

使用歸一化處理，如果數據中異常點較多，會有什么影響？

在數據中存在較多異常點的情況下，使用歸一化處理可能會受到一些影響。歸一化是將數據縮放到特定范圍內的操作，但異常點的存在可能會導致以下影響：

1. 異常點的放大：歸一化可能會導致異常點在縮放后的范圍內被放大。如果異常點的值較大，歸一化后它們可能會被映射到特定范圍的邊緣，從而導致數據在正常值范圍內分布不均勻。
2. 降低數據的區分性：異常點可能導致歸一化后的數據失去一部分原始數據的分布特征。數據特征的差異性可能被模糊化，從而降低模型的區分能力和準確性。
3. 對模型的影響：在機器學習中，模型通常會受到輸入數據的影響。異常點可能會干擾模型的訓練，使其難以捕捉正常數據的模式，導致模型的性能下降。
4. 過擬合的風險：如果異常點被放大或影響了數據的分布，模型可能會過擬合異常點，而忽略了正常數據的重要特征。

為了應對異常點對歸一化處理的影響，可以考慮以下策略：

• 異常點檢測和處理：在進行歸一化之前，首先要進行異常點檢測，并根據異常點的性質和數量采取適當的處理措施。可以選擇刪除異常點、使用異常點修正方法或將異常點映射到更合理的范圍。
• 使用魯棒性方法：某些歸一化方法對異常點的影響較小，例如中心化和縮放（例如Z-score標準化），它們對異常值的影響較小，因為它們基于數據的分布特性。
• 嘗試其他特征預處理方法：如果異常點較多且歸一化效果不好，可以嘗試其他特征預處理方法，如對數變換、截斷、縮尾等。

總之，處理異常點是特征預處理的重要步驟，需要根據數據的特點和問題的需求來選擇適當的策略。

這里使用標準化解決這個問題

4、標準化

定義：通過對原始數據進行變換把數據變換到均值為0,標準差為1范圍內

公式：

標準差：

????????

所以實際上標準化的公式為：

?????????

參數如下：

????????x為當前值

????????mean為平均值

????????N 表示數據的總個數

????????xi 表示第 i 個數據點

????????μ 表示數據的均值

歸一化的異常點：

標準化的異常點：

對于歸一化來說：如果出現異常點，影響了最大值和最小值，那么結果顯然會發生改變

對于標準化來說：如果出現異常點，由于具有一定數據量，少量的異常點對于平均值的影響并不大，從而方差改變較小。

API：

sklearn.preprocessing.StandardScaler( )

處理之后每列來說所有數據都聚集在均值0附近標準差差為1

StandardScaler.fit_transform(X)

X:numpy array格式的數據[n_samples,n_features]

返回值：轉換后的形狀相同的array

import pandas as pd
from sklearn.preprocessing import StandardScaler  # 標準化'''
sklearn.preprocessing.StandardScaler( ) 處理之后每列來說所有數據都聚集在均值0附近標準差差為1StandardScaler.fit_transform(X)X:numpy array格式的數據[n_samples,n_features]返回值：轉換后的形狀相同的array
'''
def stand_demo():"""標準化演示:return: None"""data = pd.read_csv("data/dating.txt", delimiter="\t")print(data)# 1、實例化一個轉換器類transfer = StandardScaler()# 2、調用fit_transformdata = transfer.fit_transform(data[['milage', 'Liters', 'Consumtime']])print("標準化的結果:\n", data)print("每一列特征的平均值：\n", transfer.mean_)print("每一列特征的方差：\n", transfer.var_)if __name__ == '__main__':stand_demo()

輸出結果：

手動計算驗證(取前8行數據)，公式回顧如下：

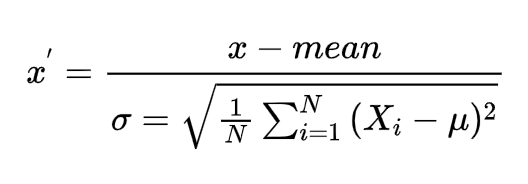
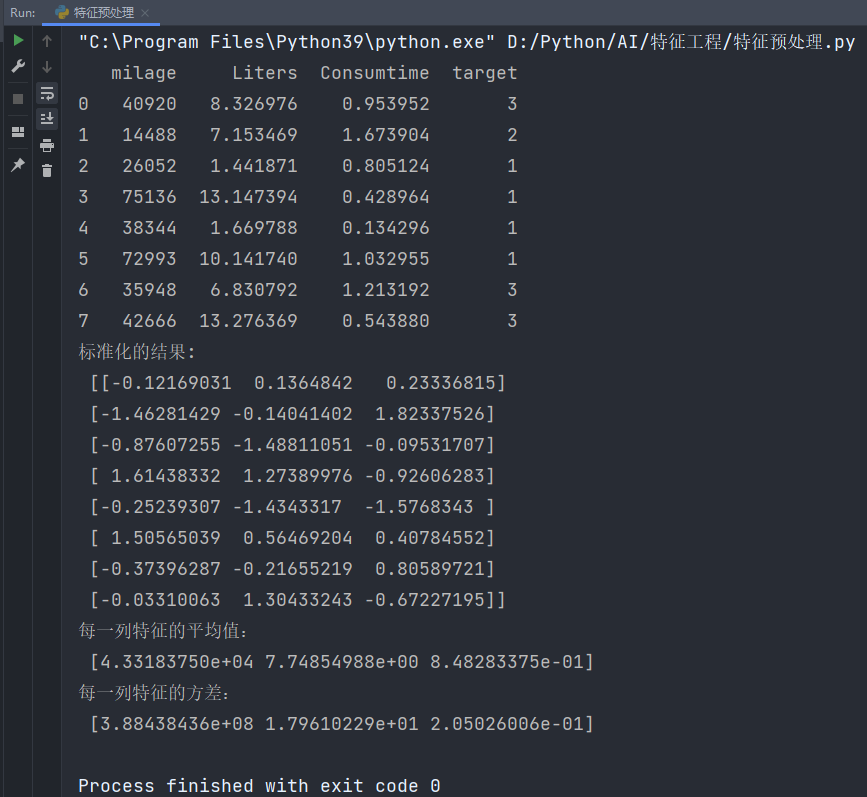
手動計算坐標為(0,0)的數據的標準化數據：

????????40920-43318.375=-2398.375

????????N=8，μ=43318.375 -> (40920-43318.375)^2+(14488-43318.375)^2+(26052-43318.375)^2+(75136-43318.375)^2+(38344-43318.375)^2+(72993-43318.375)^2+(35948-43318.375)^2+(42666-43318.375)^2=3107507487.875

????????3107507487.875 / 8 = 388438435.984375

????????根號下388438435.984375 = 19708.84156880802

最終：

????????x-mean=-2398.375

????????標準差=19708.84156880802

最后標準化后的數據結果為：-2398.375 / 19708.84156880802 = 0.121690307957813291 ≈ 0.12169031

與程序結果完全吻合！

標準化總結：在已有樣本足夠多的情況下比較穩定，適合現代嘈雜大數據場景。

?