偏差-方差分解（轉）

1、定義

這里所說的偏差-方差分解就是一種解釋模型泛化性能的一種工具。它是對模型的期望泛化錯誤率進行拆解。

樣本可能出現噪聲，使得收集到的數據樣本中的有的類別與實際真實類別不相符。對測試樣本 x，另 y_d?為 x 在數據集中的標記，y 為真實標記，f(x;D) 為訓練集D上學得模型 f 在 x 上的預測輸出。接下來以回歸任務為例：

模型的期望預測：

?

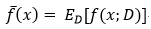
樣本數相同的不同訓練集產生的方差：

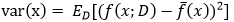
噪聲：

期望輸出與真實標記的差別稱為偏差：

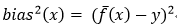
?2、推導

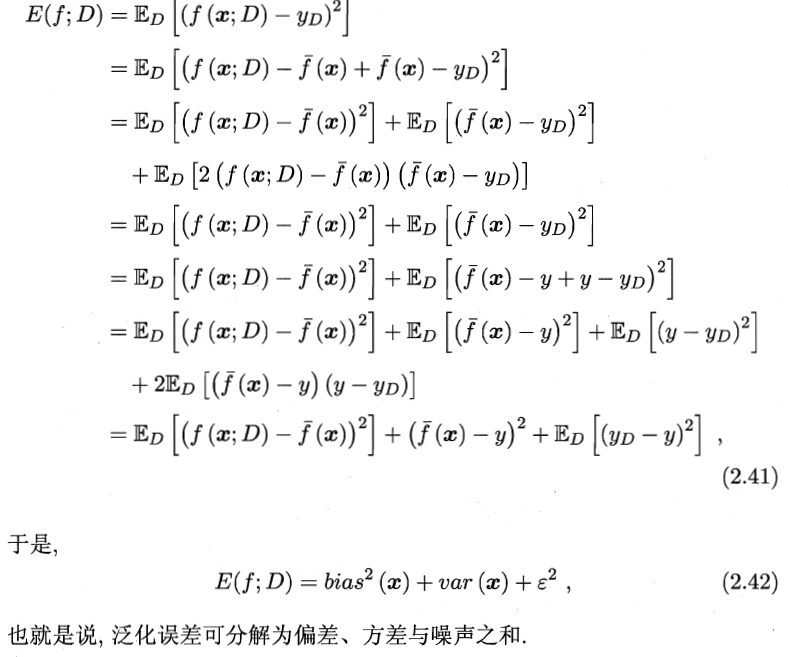
3、含義

偏差：度量了模型的期望預測和真實結果的偏離程度，刻畫了模型本身的擬合能力。

方差：度量了同樣大小的訓練集的變動所導致的學習性能的變化，即刻畫了數據擾動所造成的影響。

噪聲：表達了當前任務上任何模型所能達到的期望泛化誤差的下界，刻畫了學習問題本身的難度。

4、偏差-方差窘境

為了得到泛化性能好的模型，我們需要使偏差較小，即能充分擬合數據，并且使方差小，使數據擾動產生的影響小。但是偏差和方差在一定程度上是有沖突的，這稱作為偏差-方差窘境。

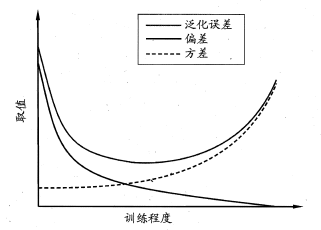
下圖給出了在模型訓練不足時，擬合能力不夠強，訓練數據的擾動不足以使學習器產生顯著變化，此時偏差主導泛化誤差，此時稱為欠擬合現象。當隨著訓練程度加深，模型的擬合能力增強，訓練數據的擾動慢慢使得方差主導泛化誤差。當訓練充足時，模型的擬合能力非常強，數據輕微變化都能導致模型發生變化，如果過分學習訓練數據的特點，則會發生過擬合。

針對欠擬合，我們提出集成學習的概念并且對于模型可以控制訓練程度，比如神經網絡加多隱層，或者決策樹增加樹深。針對過擬合，我們需要降低模型的復雜度，提出了正則化懲罰項。

?

?

轉自：https://www.cnblogs.com/hithink/p/7372470.html