滑模控制的運動軌跡主要分為兩個方面:(1)系統的任意初始狀態向滑模面運動階段;(2)系統到達滑模面后并且慢慢趨于穩定的階段。所以,對于滑模變結構控制器的設計,對應于系統運動的兩個階段,可以分為兩個部分:第一部分,滑模面的設計;第二部分,控制律的設計。
0、前言
滑模控制(Sliding Mode Control,SMC)是一種非線性控制方法,其核心思想是通過引入一個滑動模態,使系統狀態在該模態上滑動,并保持在滑動面上。滑模控制具有強魯棒性和快速響應的特點,能夠有效應對系統參數不確定性、外部干擾和測量噪聲等問題。
?
滑模控制的基本原理是通過設計一個滑動面,使系統狀態在該面上滑動,并且在滑動面上滑動的速度足夠快,從而將系統狀態迅速帶到所期望的工作區域。通常情況下,滑動面由一個或多個狀態變量的線性組合構成,可以根據實際應用需求進行選擇。
滑模控制的主要步驟包括:
-
滑動面設計:根據系統的數學模型和控制目標,設計一個合適的滑動面。滑動面應具有良好的魯棒性和適應性,能夠滿足所需的控制性能。
-
控制律設計:根據滑動面的定義,設計一個控制律使得系統狀態在滑動面上滑動。通常情況下,控制律包括兩個部分:滑動面的控制和滑模調節器。滑動面的控制用來使系統狀態迅速進入滑動模態,而滑模調節器用來保持系統狀態在滑動面上滑動。
-
控制器實現:根據設計的控制律,實現具體的控制器。控制器可以是連續時間控制器或離散時間控制器,具體選擇取決于被控系統的特性和應用需求。
滑模控制的優點包括:
-
魯棒性:滑模控制對系統的參數不確定性和外部干擾具有較強的魯棒性,能夠使系統在不確定性和擾動的影響下仍能保持滑動模態。
-
快速響應:由于滑動模態的特性,滑模控制具有快速響應的特點,能夠使系統迅速達到所期望的狀態。
-
簡單性:相對于一些復雜的控制方法,滑模控制比較簡單,容易實現和應用。
1、滑模面的設計
以電液伺服控制系統為例,電液伺服控制系統中不考慮伺服閥的非線性影響將其簡化為比例環節,所以由電液伺服系統的數學模型可得伺服閥閥芯位移到液壓缸活塞位移的傳遞函數為:
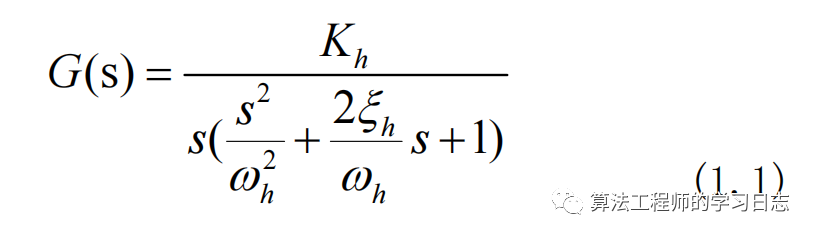
辨識后的模型為
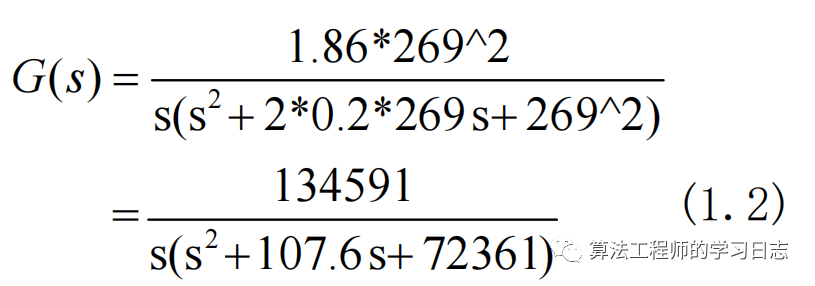
狀態空間方程為
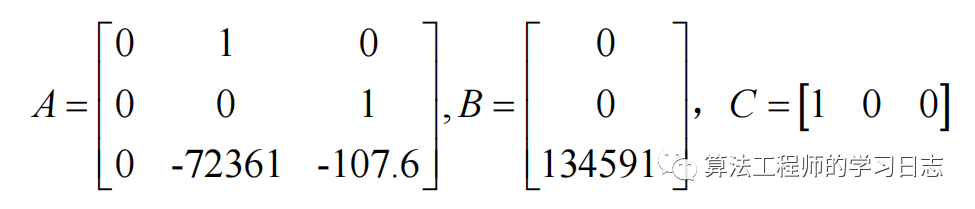
被控對象為三階系統, X = [x x' x'']為系統狀態變量。設定r為給定的輸入信號, y為系統輸出信號,所以系統的誤差為?e=r?-y,,定義系統的誤差向量為:
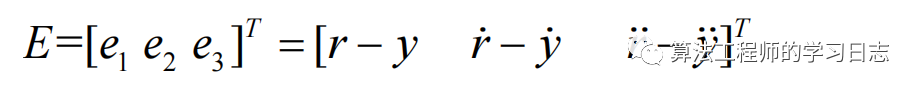
可以根據系統模型狀態空間方程
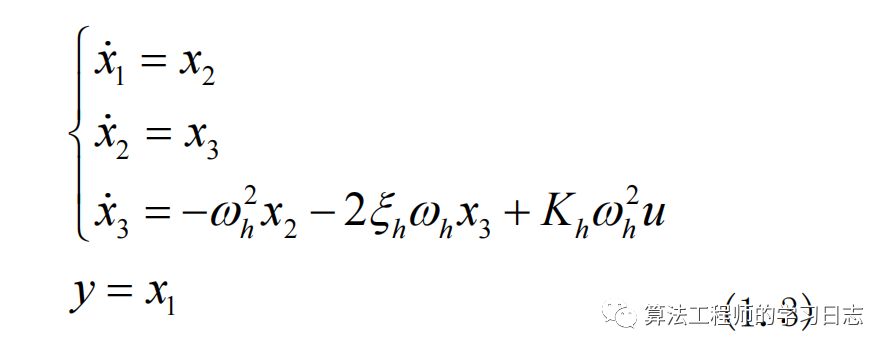
寫出誤差狀態方程
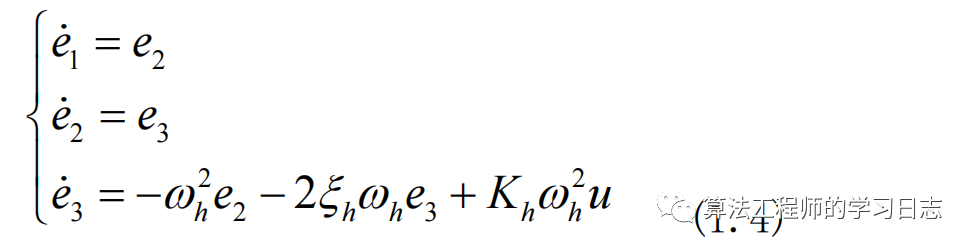
所設計的滑模切換函數為
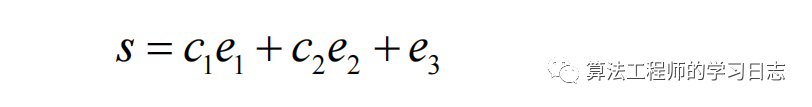
滑模運動的微分方程為
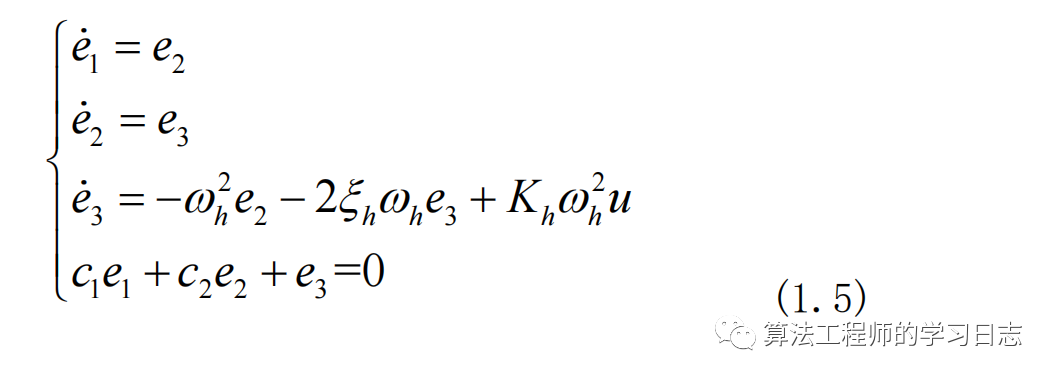
其中c1、c2決定了滑動模態的動態品質,可以采用極點置法求得c1、c2??。選擇期望極點為-34.4±168.52i,可以得到參數?c1=29582, c2=68.8,?
2、控制器的設計
對于滑模變結構控制器的設計如下:?
u=ueq+usw
ueq是等效控制,能夠實現系統狀態的跟蹤,即將系統的狀態一直保持在滑模面上;?usw是切換控制,使系統狀態趨近于滑模面,削弱系統的抖振,常用的趨近率有三種:
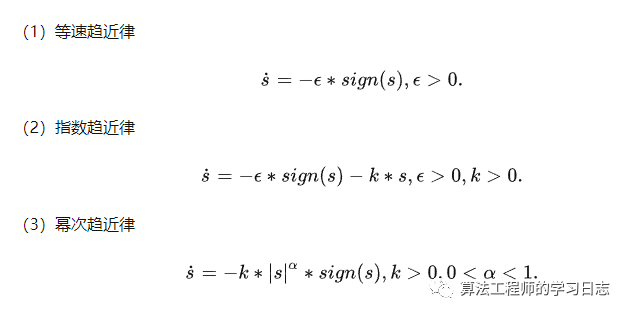
本節將采用指數趨近律,
等效控制部分,對s=c1*e1+c2*e2+e3求導得
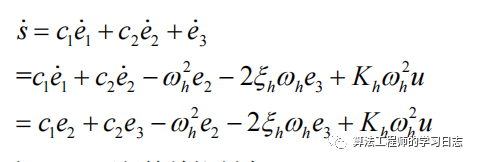
根據s'=0可得到等效控制:
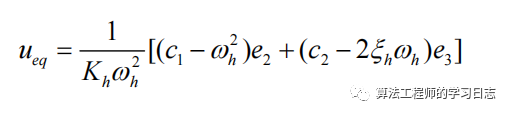
切換控制部分,選擇指數趨近律,即
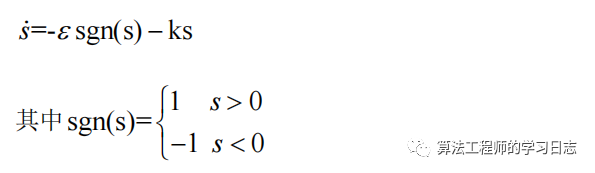
假如eta過小,那么趨近的速度很慢,調節的過程太慢;相反,若eta太大,那么系統到達切換面的時候,具有比較大的速度,引起較大的抖動。對于 k,能夠加快調節時間,能夠快速到達滑模面的過程,還可以削弱抖振,改善系統的品質。本文中,指數趨近律的參數 k 為 20,?eta為 5。所以切換控制為:
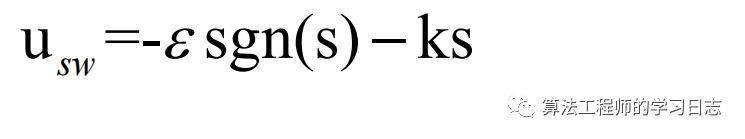
綜上所述,滑模變結構的控制器設計為
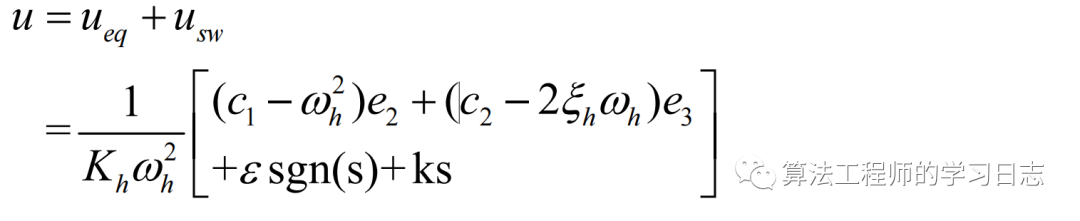
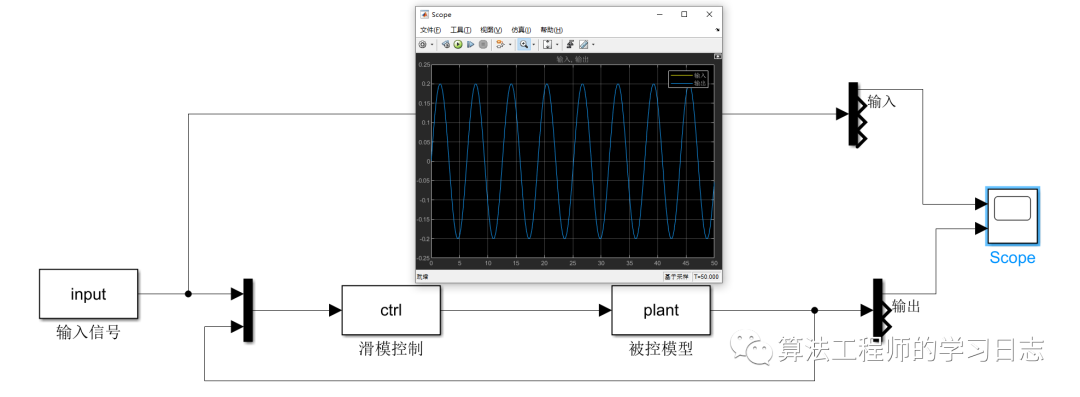
3、實例建模和分析
在matlab simulink中用sfunction搭建對應的仿真模型
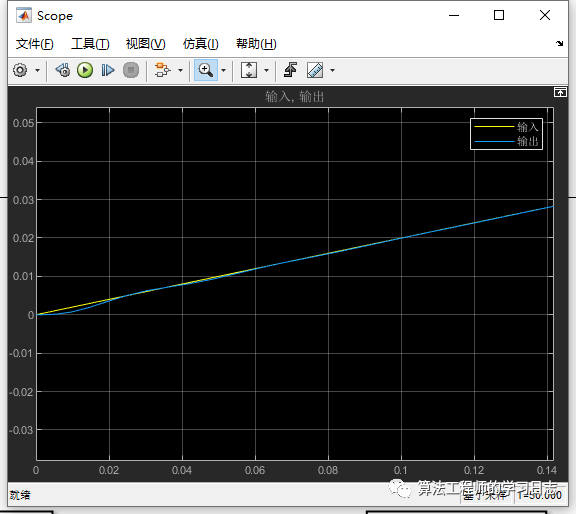
放大結果圖,可以看到在滑模控制能夠很快的實現輸入跟蹤,控制效率極高


面向對象編程 OOP)



)





)






