概率圖模型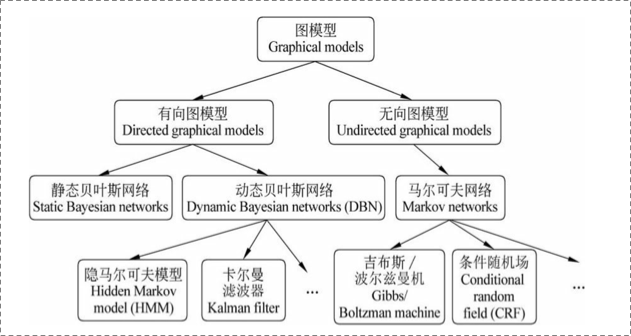
HMM
先從一個具體的例子入手,看看我們要解決的實際問題.例子引自wiki.https://en.wikipedia.org/wiki/Hidden_Markov_model
Consider two friends, Alice and Bob, who live far apart from each other and who talk together daily over the telephone about what they did that day. Bob is only interested in three activities: walking in the park, shopping, and cleaning his apartment. The choice of what to do is determined exclusively by the weather on a given day. Alice has no definite information about the weather, but she knows general trends. Based on what Bob tells her he did each day, Alice tries to guess what the weather must have been like.
Alice believes that the weather operates as a discrete Markov chain. There are two states, "Rainy" and "Sunny", but she cannot observe them directly, that is, they are hidden from her. On each day, there is a certain chance that Bob will perform one of the following activities, depending on the weather: "walk", "shop", or "clean". Since Bob tells Alice about his activities, those are the observations. The entire system is that of a hidden Markov model (HMM).
簡單翻譯一下:Alice和Bob住在兩地,每天電話溝通.Bob只對三件事有興趣:逛公園,購物,打掃房間.Bob根據天氣安排自己每日的活動.Alice知道bob每天都干嘛,以此為基礎,她可以推測出Bob所在地區的天氣.Alice認為天氣預測就是一個馬爾科夫鏈.天氣有兩種狀態,Rainy/Sunny,由于她無法直接觀測到天氣狀態,天氣對她而言是隱藏的.
馬爾科夫假設:
假設模型的當前狀態僅僅依賴于前面的幾個狀態,這被稱為馬爾科夫假設,它極大地簡化了問題。顯然,這可能是一種粗糙的假設,并且因此可能將一些非常重要的信息丟失。
一個馬爾科夫過程是狀態間的轉移僅依賴于前n個狀態的過程。這個過程被稱之為n階馬爾科夫模型,其中n是影響下一個狀態選擇的(前)n個狀態。
最簡單的馬爾科夫過程是一階模型,它的狀態選擇僅與前一個狀態有關.
比如今天的天氣和昨天的天氣有關.如下:
隱藏馬爾科夫
回到我們的例子,當我們有足夠多的天氣資料以后,我們是可以根據昨天的天氣推測出最有可能的的今天的天氣的.比如昨天晴天,那求p(晴天|晴天),p(陰天|晴天)的概率,取二者之中較大的一個即可.
這個例子里天氣狀況我們稱之為狀態,相應的概率矩陣稱之為狀態轉移矩陣.一個有M個狀態的馬爾科夫模型有\(M^2\)個狀態轉移.
現在我們定義一個一階馬爾科夫過程如下: 狀態:三個狀態——晴天,多云,雨天。 pi向量:定義系統初始化時每一個狀態的概率。 狀態轉移矩陣:給定前一天天氣情況下的當前天氣概率。
任何一個可以用這種方式描述的系統都是一個馬爾科夫過程。
但是考慮我們的例子中,Alice雖然每日與Bob通話,但是Bob并不會告訴他當地天氣情況,只會告訴他自己每天干了啥(逛公園/購物/打掃房間等).所以天氣狀態對Alice來說是隱藏(Hidden)的,Alice并不知道每日天氣,他能事先知道的只有陰天后,第二天是陰天/晴天的概率,即狀態轉移矩陣。
天氣狀態是隱藏狀態,Bob的每日活動(逛公園/購物/打掃房間)是觀察狀態.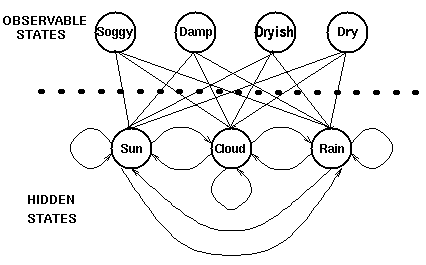
圖文不符,湊合看,領會意圖....假裝soggy/damp/...代表逛公園/購物/打掃房間....
對每一種隱藏狀態,都有與之對應的觀測狀態,和前面的狀態轉移概率矩陣一樣,我們有如下的概率矩陣稱之為混淆矩陣: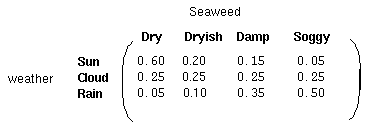
至此,一個HMM模型所包含的要素如下:
- 隱藏狀態
- 觀測狀態
- pi向量 模型初始隱藏狀態的概率
- 轉移矩陣:狀態轉移的概率矩陣
- 混淆矩陣(有的翻譯成發射概率矩陣):隱藏狀態與觀察狀態的對應概率矩陣
alice預測bob所在地區天氣用HMM建模可以表達如下:
#隱藏狀態states = ('Rainy', 'Sunny')#觀測狀態observations = ('walk', 'shop', 'clean')#初始pi向量start_probability = {'Rainy': 0.6, 'Sunny': 0.4}#狀態轉移矩陣transition_probability = {'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},}#混淆矩陣.比如如下數據代表陰天時,bob有0.1的概率逛公園,0.4的概率散步,0.5的概率做清潔.emission_probability = {'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},}HMM解決的三個基本問題
- 給定HMM求一個觀察序列的概率(評估) 使用前向算法解決
- 搜索最有可能生成一個觀察序列的隱藏狀態序列(解碼)使用維特比算法解決
- 是給定觀察序列生成一個HMM(學習)使用前向-后向算法解決
對應到alice-bob的例子里即我們通過大量樣本的訓練已經得到了一個HMM的model.
Alice和Bob通了三天電話后發現第一天Bob去散步了,第二天他去購物了,第三天他清理房間了。Alice現在有兩個問題:
- 這個觀察序列“散步、購物、清理”的總的概率是多少?(注:這個問題對應于HMM的基本問題之一:已知HMM模型λ及觀察序列O,如何計算P(O|λ)?)
- 最能解釋這個觀察序列的狀態序列(晴/雨)又是什么?(注:這個問題對應HMM基本問題之二:給定觀察序列O=O1,O2,…OT以及模型λ,如何選擇一個對應的狀態序列S = q1,q2,…qT,使得S能夠最為合理的解釋觀察序列O?)
- 至于HMM的基本問題之三:如何調整模型參數, 使得P(O|λ)最大?這個問題事實上就是給出很多個觀察序列值,來訓練以上幾個參數的問題。
算法
- 前向算法
- 維特比算法
- 前向-后向算法
HMM應用
- 詞性標注
- 中文分詞
HMM與CRF關系
比如要給"i love you"進行詞性標注.
那么HMM中的"隱藏狀態"即為詞性(名詞/動詞/形容詞/...)
HMM中的"觀測狀態"即為我們看到的具體的詞(i/love/you)
實際上我們要做的就是求解p(l,s)哪種l使其最大?
其中s="i love u",對l1=(名詞/動詞/名詞),我們可以計算出一個p1=p(l1,s),對l2=(名詞/名詞/名詞),我們可以計算出一個p2=p(l2,s).自然地,對一個模型來說,應該算出的是p1>p2. 那么我們就把"i love u"標注為"名詞/動詞/名詞"
如何計算p(l,s)
還是以上面的"i love u"為例,l=(名詞/動詞/名詞)
- p(li|li?1) 狀態轉移概率 (比如l2=動詞,l1=名詞,則代表名詞后面接動詞的概率);
- p(wi|li) 發射概率(也就是之前例子里說的混淆矩陣概率) (比如l2=動詞 w2="love" 代表一個動詞是單詞"love"的概率)
注意我們在條件隨機場https://www.cnblogs.com/sdu20112013/p/10370334.html里提到的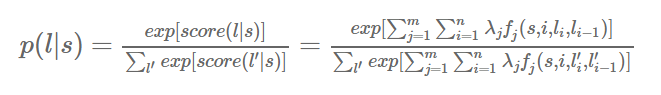
對一個HMM來說,對概率取對數可得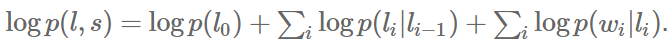
我們可以構建一個等價于該HMM的CRF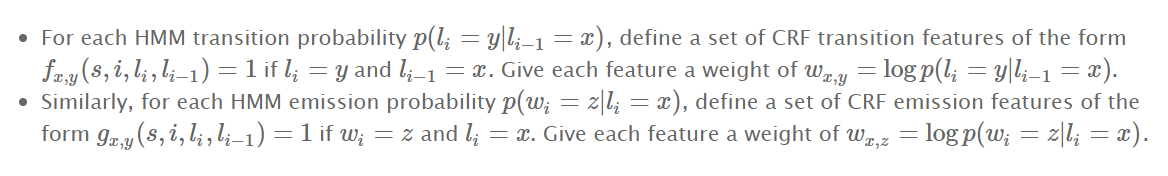
- 對每一個狀態轉移概率,都可以創建一個特征函數f,給一個權重w
- 對每一個發射概率,也可以定一個特征函數g,給一個權重w
這樣crf計算出來的p(l,s)和HMM計算出來的p(l,s)就等價了.
也就是說每一個HMM都可以用某一個CRF來表達
crf比HMM更強大
- crf可以定制更多的特征函數 比如對"is that ok?"做詞性標注.用crf的話,我們可以定義一個特征函數:一個以?結尾的句子的第一個單詞更可能是動詞. 在HMM中我們沒辦法表達這個信息. 從而crf的標注的準確率可以更高.
- crf可以有更多樣的權重. hmm里權重是可以任意的,正的,負的都可以.










)








