Task1? 賽題理解

一、學習知識點概要

本次學習先是介紹了賽題的背景和概況，題目以金融風控中的個人信貸為背景，給所給的47列特征中，根據貸款申請人的數據信息預測其是否有違約的可能，以此判斷是否通過貸款。隨后介紹了比賽中的評價指標，出現的相關知識點有：

1.混淆矩陣（Confuse Matrix）

2.準確率（Accuracy）

3.精確率（Precision）

4.召回率（Recall）

5.F1 Score

6.P-R曲線（Precision-Recall Curve）

7.ROC（Receiver Operating Characteristic）

8.AUC(Area Under Curve)

9.KS(Kolmogorov-Smirnov)

二、學習內容

1.混淆矩陣（Confuse Matrix）

混淆矩陣是什么呢？混淆矩陣是數據科學、數據分析和機器學習中總結分類模型預測結果的情形分析表，以矩陣的形式將數據集中的記錄按照真實的類別與分類模型作出的分類判斷兩個標準進行匯總。這個名字來源于它可以非常容易的表明多個類別是否有混淆。用于得出分類正確和錯誤的樣本數量。一般的混淆矩陣是n×n的。

在我們要解的二元分類問題（即判斷一個東西是不是我們所認為的東西）中，混淆矩陣通常是2×2的。我們可以將分類的結果歸為正類和負類（或陽性和陰性），先用我們構建出來的預測模型將樣本進行分類，然后再查看樣本的真實分類，將對比結果放入矩陣中。判斷結果歸類如下：

• （1）若一個實例是正類，并且被預測為正類，即為真正類TP(True Positive )
• （2）若一個實例是正類，但是被預測為負類，即為假負類FN(False Negative )
• （3）若一個實例是負類，但是被預測為正類，即為假正類FP(False Positive )
• （4）若一個實例是負類，并且被預測為負類，即為真負類TN(True Negative ）

矩陣中數據的填寫可看下圖

矩陣中的數據便為被判斷為該種結果的樣本個數。

2.混淆矩陣的延伸概念

單用一個混淆矩陣無法對模型進行準確全面的評價，由此延伸出與混淆矩陣相關的概念，有：準確率（Accuracy）、精確率（Precision）、召回率（Recall）、F1 Score、P-R曲線

其計算公式如下：

注意：準確率并不適用于樣本不均衡的情況

關于F1 Score的作用，精確率和召回率是相互影響的，精確率升高則召回率下降，召回率升高則精確率下降，如果需要兼顧二者，就需要精確率、召回率的結合F1 Score

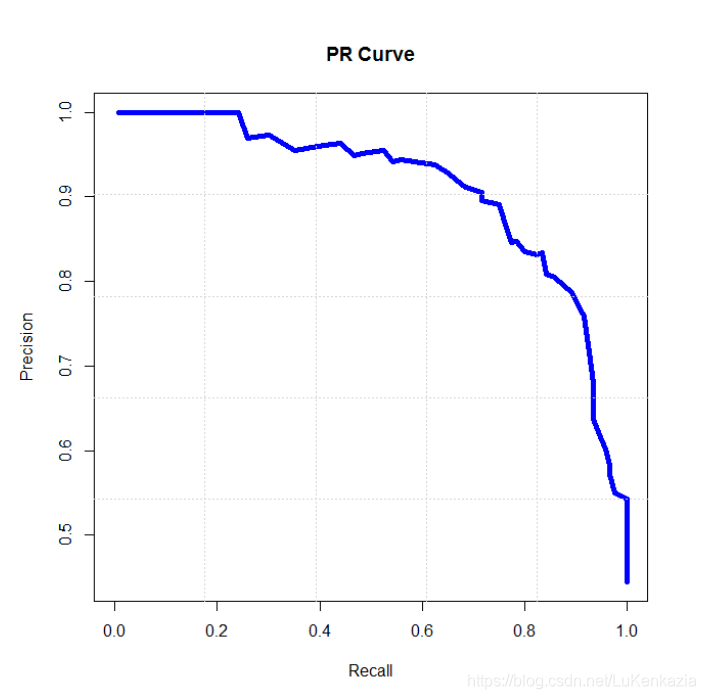
P-R曲線：P-R曲線是描述精確率和召回率變化的曲線，召回率為橫軸，精確率為縱軸。模型在為樣本分類時會有一個置信度，即表示該樣本是正樣本的概率。通過置信度就可以對所有樣本進行排序，再逐個樣本的選擇一個閾值，在該樣本之前的都屬于正例，該樣本之后的都屬于負例。每一個樣本作為劃分閾值時，都可以計算對應的precision和recall，那么就可以以此繪制曲線。

3.ROC（Receiver Operating Characteristic）

ROC為一種曲線，以兩種新出現的指標分別作為橫軸和縱軸。ROC將假正例率（FPR）定義為 X 軸，真正例率（TPR）定義為 Y 軸。

FPR：在所有實際為陰性的樣本中，被錯誤地判斷為陽性之比率 。

?

TPR：在所有實際為陽性的樣本中，被正確地判斷為陽性之比率。

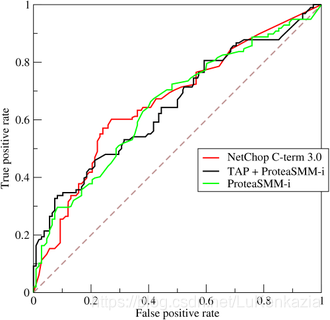
ROC曲線的作用：

I.ROC曲線能很容易的查出任意閾值對學習器的泛化性能影響。

II.有助于選擇最佳的閾值（如何選擇本次不做描述）。ROC曲線越靠近左上角，模型的準確性就越高。最靠近左上角的ROC曲線上的點是分類錯誤最少的最好閾值，其假正例和假反例總數最少。

III.可以對不同的學習器比較性能。將各個學習器的ROC曲線繪制到同一坐標中，直觀地鑒別優劣，靠近左上角的ROC曲所代表的學習器準確性最高。

4.AUC（Area Under Curve）

AUC（Area Under Curve）被定義為ROC曲線下的面積。我們往往使用AUC值作為模型的評價標準是因為很多時候ROC曲線并不能清晰的說明哪個預測模型的效果更好，而作為一個數值，對應AUC更大的預測模型效果更好。

AUC就是曲線下面積，在比較不同的分類模型時，可以將每個模型的ROC曲線都畫出來，比較曲線下面積做為模型優劣的指標。ROC 曲線下方的面積(Area under the Curve)，其意義是：

（1）因為是在1x1的方格里求面積，AUC必在0~1之間。

（2）假設閾值以上是陽性，以下是陰性；

（3）若隨機抽取一個陽性樣本和一個陰性樣本，分類器正確判斷陽性樣本的值高于陰性樣本的概率 = AUC 。

（4）簡單說：AUC值越大的分類器，正確率越高。

從AUC 判斷分類器（預測模型）優劣的標準：

• AUC = 1，是完美分類器。

• AUC = [0.85, 0.95], 效果很好

• AUC = [0.7, 0.85], 效果一般

• AUC = [0.5, 0.7],效果較低，但用于預測股票已經很不錯了

• AUC = 0.5，跟隨機猜測一樣（例：丟銅板），模型沒有預測價值

5.KS(Kolmogorov-Smirnov)

在數理統計中，可用于檢驗數據是否符合某種分布。在風控中，KS常用于評估模型區分度。區分度越大，說明模型的風險排序能力（ranking ability）越強。 K-S曲線與ROC曲線類似，不同在于K-S曲線將真正例率和假正例率都作為縱軸，橫軸則由選定的閾值來充當。 公式為：

一般情況KS值越大，模型的區分能力越強，但是也不是越大模型效果就越好，如果KS過大，模型可能存在異常。一般的評判標準如下：

KS	區分能力
0.2以下	基本無區分能力
[0.2,0.4]	一般
(0.4,0.5]	良好
(0.5,0.6]	較強
(0.6,0.75]	非常強
0.75以上	過高，存疑

?

三、學習問題與解答

初次看Task1的時候，一下子冒出很多沒見過的知識和名詞感覺頭都暈乎乎的。雖然里面已經列出了好一些概念，但是它的定義、用來干什么、怎么用都還需要自己在去查，去學習。比如一開始看到混淆矩陣，TP、TN、FN、FP到底是什么意思單看是Task1很難看明白，在百度上搜了之后也還是迷迷糊糊，最后還是查找了各種文章學習之后才知道混淆矩陣的作用以及混淆矩陣該怎么樣寫。

現在出現的問題還有很多，比如后面的Python代碼還沒看明白，P-R曲線的閾值怎么選取，以及選取閾值出來的作用是什么都不是很明白，對這些知識還沒有系統的了解。

四、學習思考與總結

思考下來就是需要學習的東西還有很多，雖說是金融風控0基礎的訓練營，但是對我這種在Task1里出現的知識和Python真正0基礎的人來說挑戰還是蠻大的。了解到的這些知識也不系統，而且也是一知半解，以后還需要多多與別人交流和學習。