OO_BLOG3_規格化設計（JML學習）

目錄

• JML語言學習筆記
  • 理論基礎
  • 應用工具鏈情況
  • JMLUnit/JMLUnitNG
• UNIT3 作業分析
  • 作業 3-1 實現兩個容器類Path和PathContainer
  • 作業 3-2 實現容器類Path和數據結構類Graph
  • 作業 3-3 實現容器類Path，地鐵系統類RailwaySystem
• 規格撰寫的心得與體會
• 最后，衷心感謝為這門課程辛苦付出的老師和助教。???

JML語言學習筆記

理論基礎

1. 注釋結構

2. JML表達式

• 原子表達式，量化表達式，集合表達式，操作符，etc.

3. 方法規格

• 前置條件(pre-condition)
• 后置條件(post-condition)
• 副作用范圍限定(side-effects)

4. 類型規格

• 不變式(invariant)
• 狀態變化約束(constraint)

應用工具鏈情況

1. OpenJML & SMT Solver

• 首先由OpenJML將JML規格轉換乘SMT-LIB格式的代碼，然后調用SMT solver進行檢查。用于靜態檢查。

2. JMLUnitNG

• 根據規格自動生成測試文件。用于自動測試。

3. JMLdoc

• 可以快速生成JML文檔的相關文件

4. Junit

• Junit主要用于單元化測試與一定的自動化測試，配合JML食用效果極佳。

JMLUnit/JMLUnitNG

1. 前期準備

• 簡單代碼示例與jar包配置

2. 命令行操作

java -jar jmlunitng.jar src/Demo.java 
javac -cp jmlunitng.jar src/*.java

3. 測試結果

4. 結果分析

• 我們可以看出，自動生成的測試樣例對各種極端情況進行了測試，具有較好的覆蓋性。
• 但是，在試驗過程中，JML測試的局限性也被暴露出來了。

UNIT3 作業分析

作業 3-1 實現兩個容器類Path和PathContainer

1. 架構設計

1）度量分析

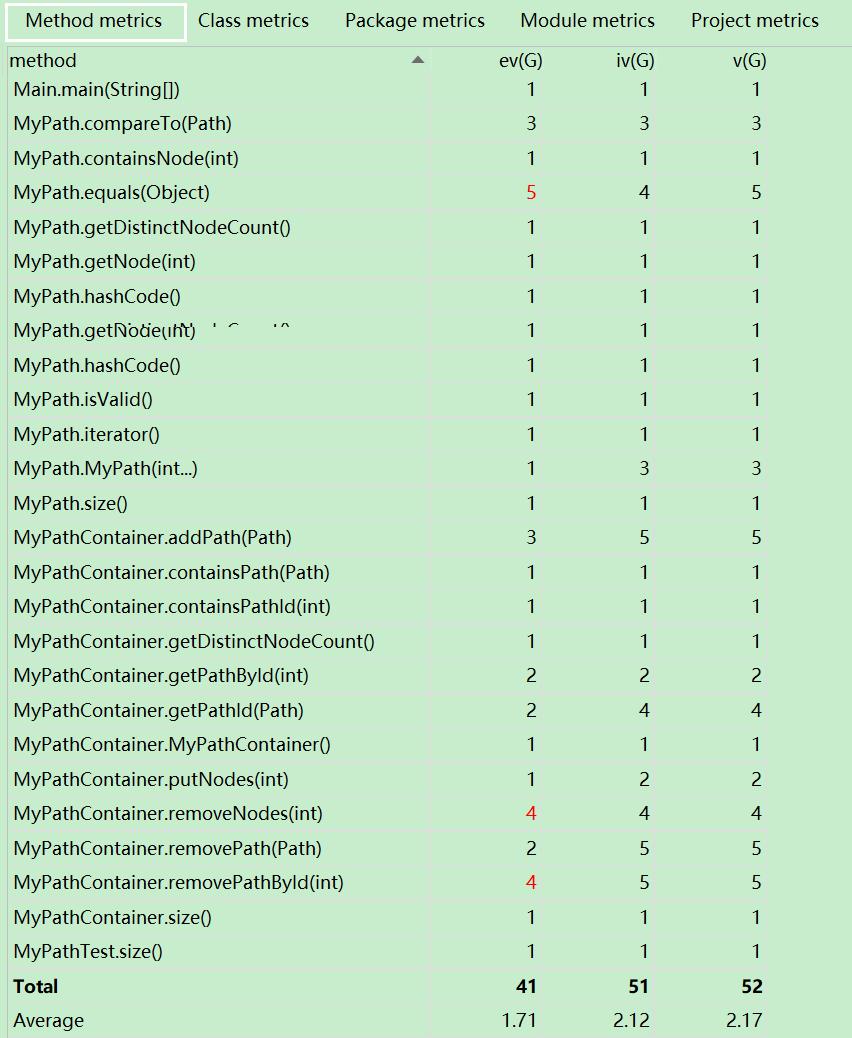
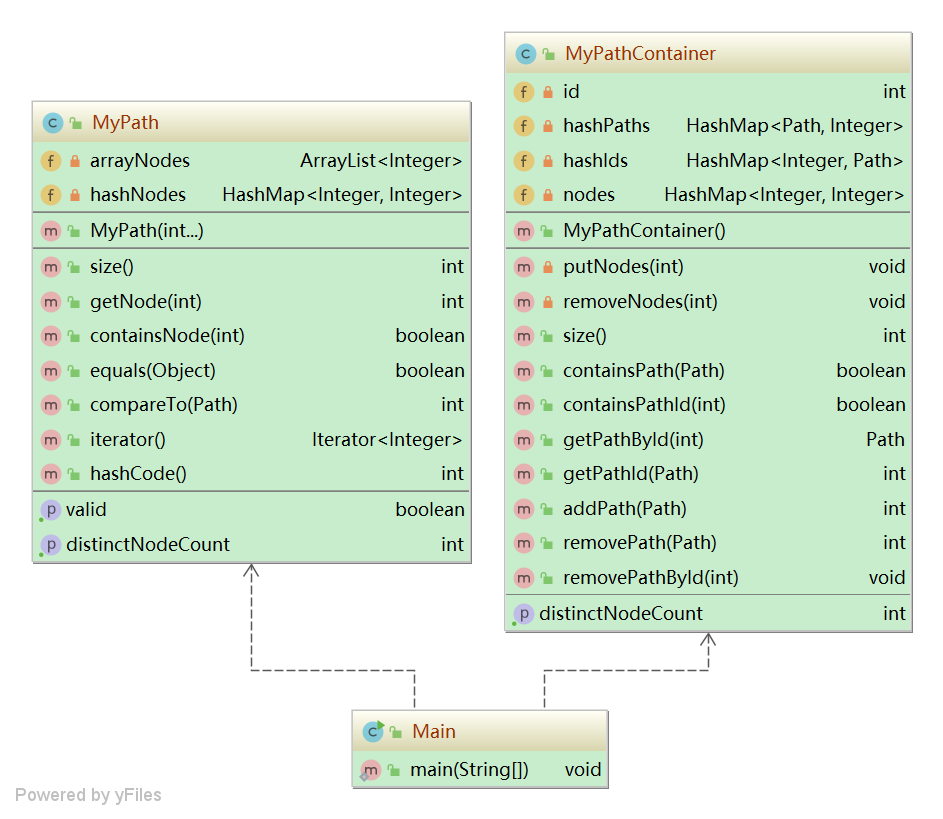
2）結構分析

3）算法分析

• MyPath

  • // path的存儲結構，用來順序存儲結點
    private ArrayList<Integer> arrayNodes; 
    // 用來存儲一條path中的node的個數（無重復）。key：結點名稱；value：該結點出現的次數
    private HashMap<Integer, Integer> hashNodes; 

  • ADD：
    1）讀入一個結點數組
    2）將結點順序存入arrayNodes
    3）遍歷結點數組，對于任一結點node，若node不在hashNodes中，即存入(node, 1)；若已存在，即存入(node, value + 1)。

• MyPathContainer

  • private int id = 0; // pathID
    private HashMap<Path, Integer> hashPaths; // Path --> PathID
    private HashMap<Integer, Path> hashIds; // PathID --> Path
    private HashMap<Integer, Integer> nodes; // Node --> frequentNumber

  • ADD:
    原理與path相同REMOVE：
    1）hashIds.remove(pathID)，hashPaths.remove(path)
    2）對于path中的每一個node，（設node的出現次數為frequentNumber），若frequentNumber=1，則將node從nodes中移除；若frequentNumber>1，則 nodes.replace(node, frequentNumber-1)。

2. BUG分析

1）bug情況

• 由于測試數據量的限制，程序在評測與互測環節沒有出現錯誤。

2）修復情況

• 該程序存在一些不優美的地方，如MyPath中，利用HashMap來存儲不同結點是復雜的，可以說是自己造了個輪子，改正方法為使用HashSet進行存儲，通過容器的特性來減少手動判斷。

---

作業 3-2 實現容器類Path和數據結構類Graph

1. 架構設計

1）度量分析

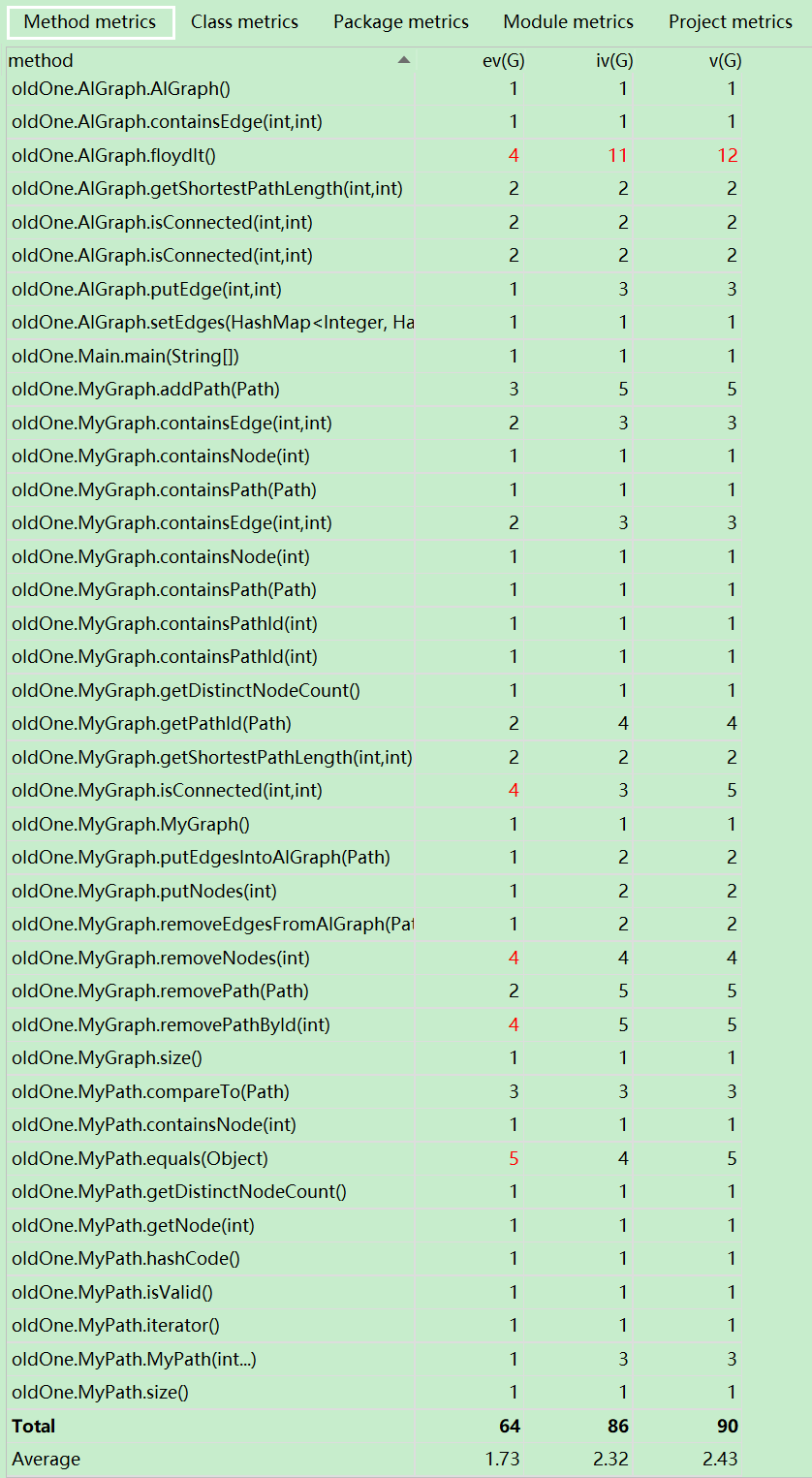
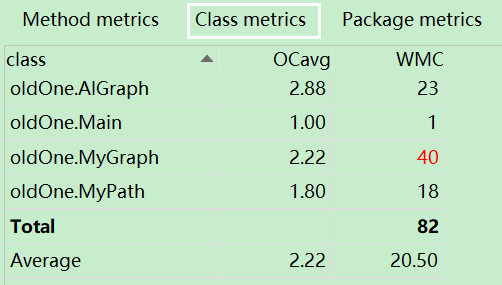
2）結構分析

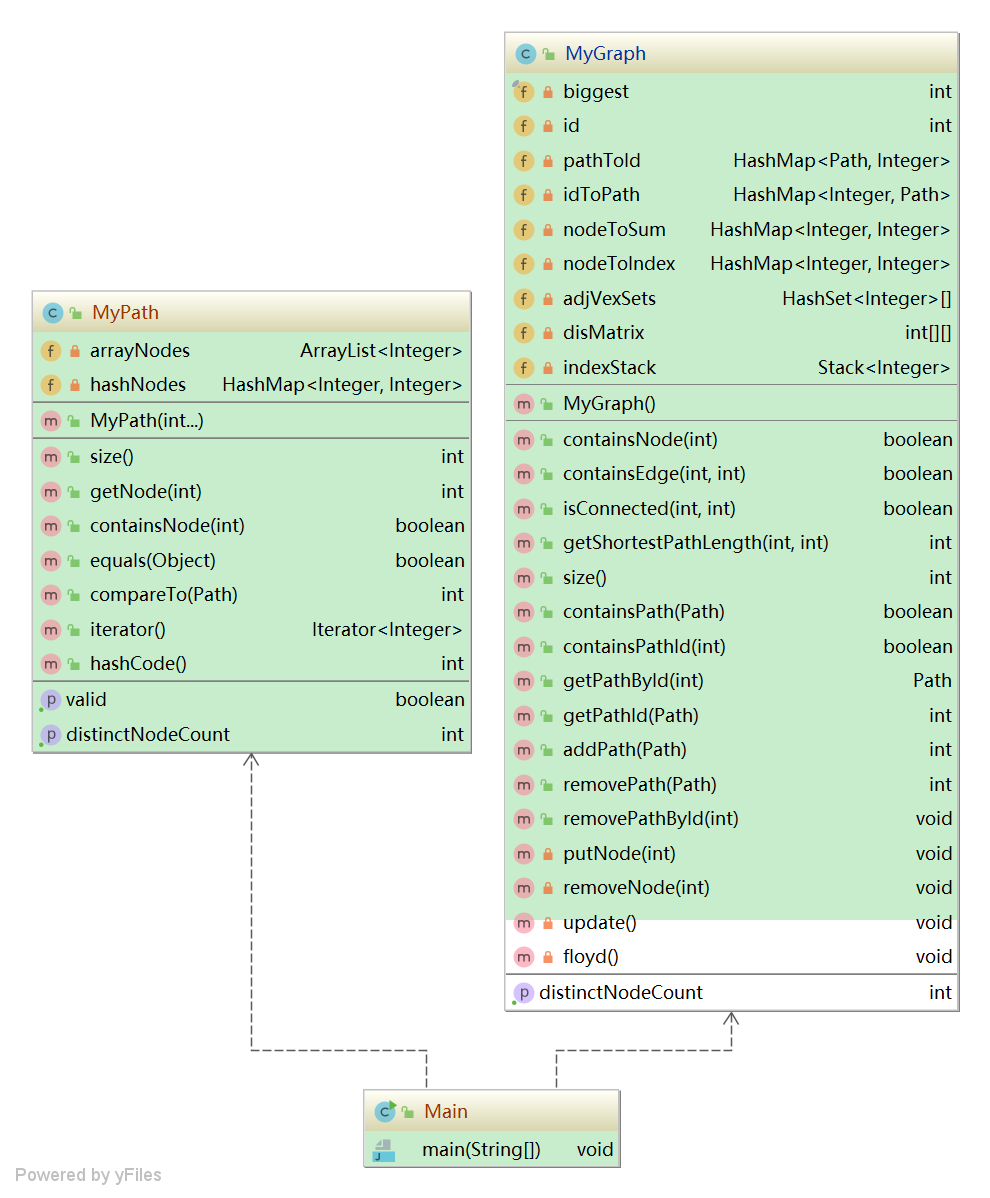
3）算法分析

• AlGraph

  • // alGraph: node1 --> (node2 -> node2_frequentNumber)
    private HashMap<Integer, HashMap<Integer, Integer>> alGraph; 
    // edges: node1 --> (node2 -> shortestPathLength_From_Node1_To_Node2)
    private HashMap<Integer, HashMap<Integer, Integer>> edges; 

  • // 由原始圖（alGraph）生成距離圖（edges）的算法 ———— Floyd算法
    for (k = 0; k< MAX; k++) for (i = 0; i < MAX; i++) for (j = 0; j < MAX; j++) if (Graph[i][j] > Graph[i][k] + Graph[k][j]) Graph[i][j] = Graph[i][k] + Graph[k][j];
    

  • public boolean containsEdge(int node1, int node2) {return alGraph.get(node1).containsKey(node2);
    }
    public boolean isConnected(int node1, int node2) {if (node1 == node2) return true;else                return edges.get(node1).containsKey(node2);
    }
    public int getShortestPathLength(int node1, int node2) {if (node1 == node2) return 0;else                return edges.get(node1).get(node2);
    }

4）迭代中對架構的重構

• AlGraph繼承了上一次作業中的PathContainer，并進行了適當的擴充（具體擴充見如上算法分析）。

2. BUG分析

1）bug情況

• 測試數據量增大時，程序出現 CPU_TIME_LIMIT_EXCEED 的錯誤。
• 原因（據我分析）：在Floyd算法中加入的大量的判斷，當數據量增大時，造成CPU的負擔過大，運算超時。

2）修復情況

• 重構后UML圖

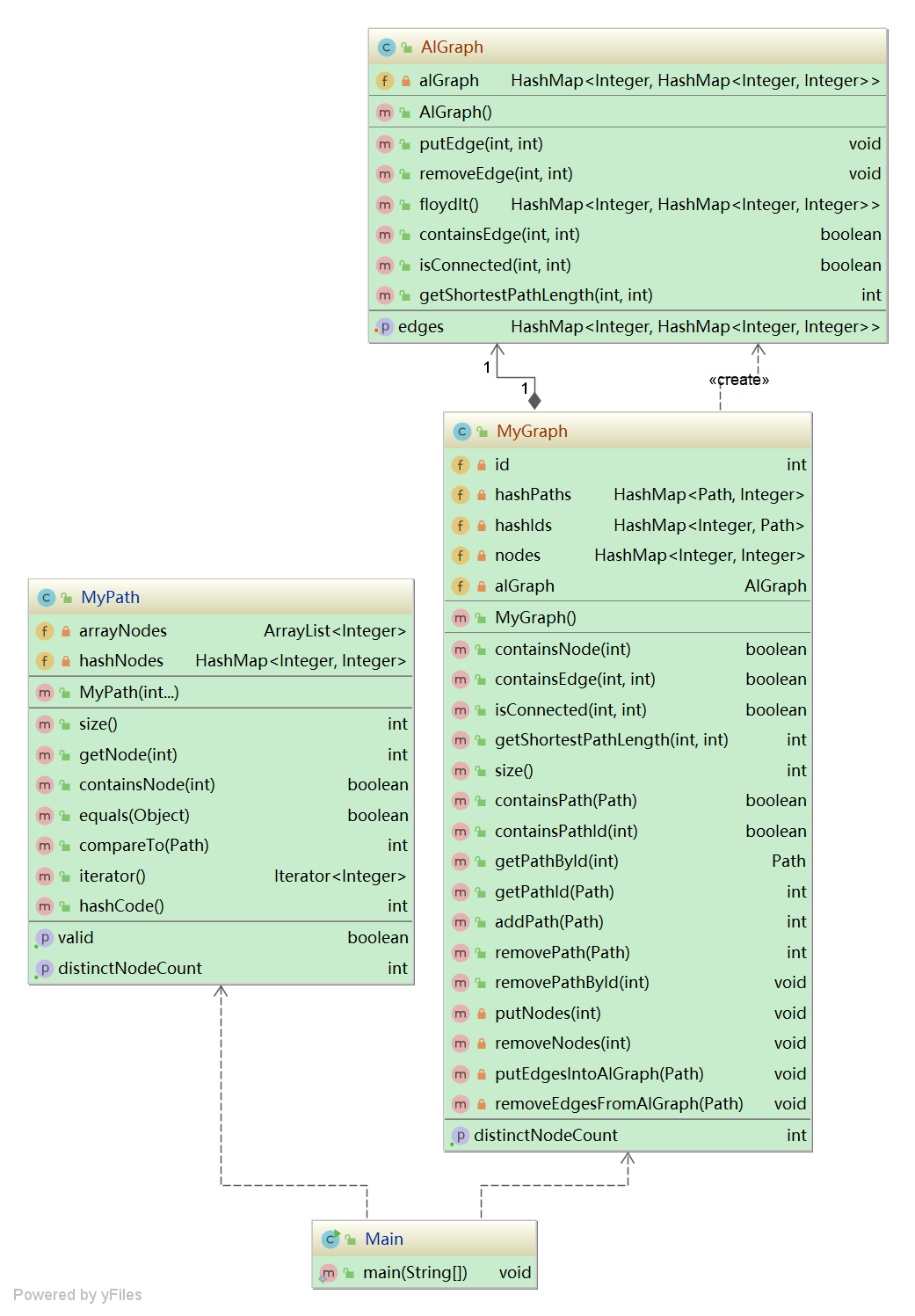
• 算法分析

  • private final int biggest = 999999999; // 極大數（自由定義，小于2^31即可）
    private int id = 0; // PathID（同上一次作業）
    private HashMap<Path, Integer> pathToId; // Path --> PathID（同上一次作業）
    private HashMap<Integer, Path> idToPath; // PathID --> Path（同上一次作業）
    private HashMap<Integer, Integer> nodeToSum; // Node --> Node_Sum（同上一次作業）
    private HashMap<Integer, Integer> nodeToIndex; // Node --> Node_index_in_matrix
    private HashSet<Integer>[] adjVexSets; // 臨界表：Node--Set{node1, node2, ...}
    private int[][] disMatrix; // Graph生成的存儲各點之間距離的距離矩陣
    private Stack<Integer> indexStack; // 用來維護node<->index的映射的棧

  • '映射關系建立機制，搭建點與數組下標的關系
    if      put_New_Node_Into_Graph then bond_NewNode_to_IndexStack.pop() 
    else if remove_Node_From_Graph  then indexStack.push(oldNode.index)

3）前后對比

• // 原程序，floyd部分代碼
  for (int k : tempEdges.keySet()) for (int i : tempEdges.keySet()) for (int j : tempEdges.keySet()) if (tempEdges.get(i).containsKey(k) && tempEdges.get(k).containsKey(j)) { int via = tempEdges.get(i).get(k) + tempEdges.get(k).get(j);if (tempEdges.get(i).containsKey(j)) {if (tempEdges.get(i).get(j) > via) {tempEdges.get(i).replace(j, via);}} else {tempEdges.get(i).put(j, via);}}

• // 重構后，floyd部分代碼
  for (int k = 0; k < 255; k++) for (int i = 0; i < 255; i++) for (int j = 0; j < 255; j++) if (disMatrix[i][j] > (newDis = disMatrix[i][k] + disMatrix[k][j])) disMatrix[i][j] = newDis;

---

作業 3-3 實現容器類Path，地鐵系統類RailwaySystem

1. 架構設計

1）度量分析

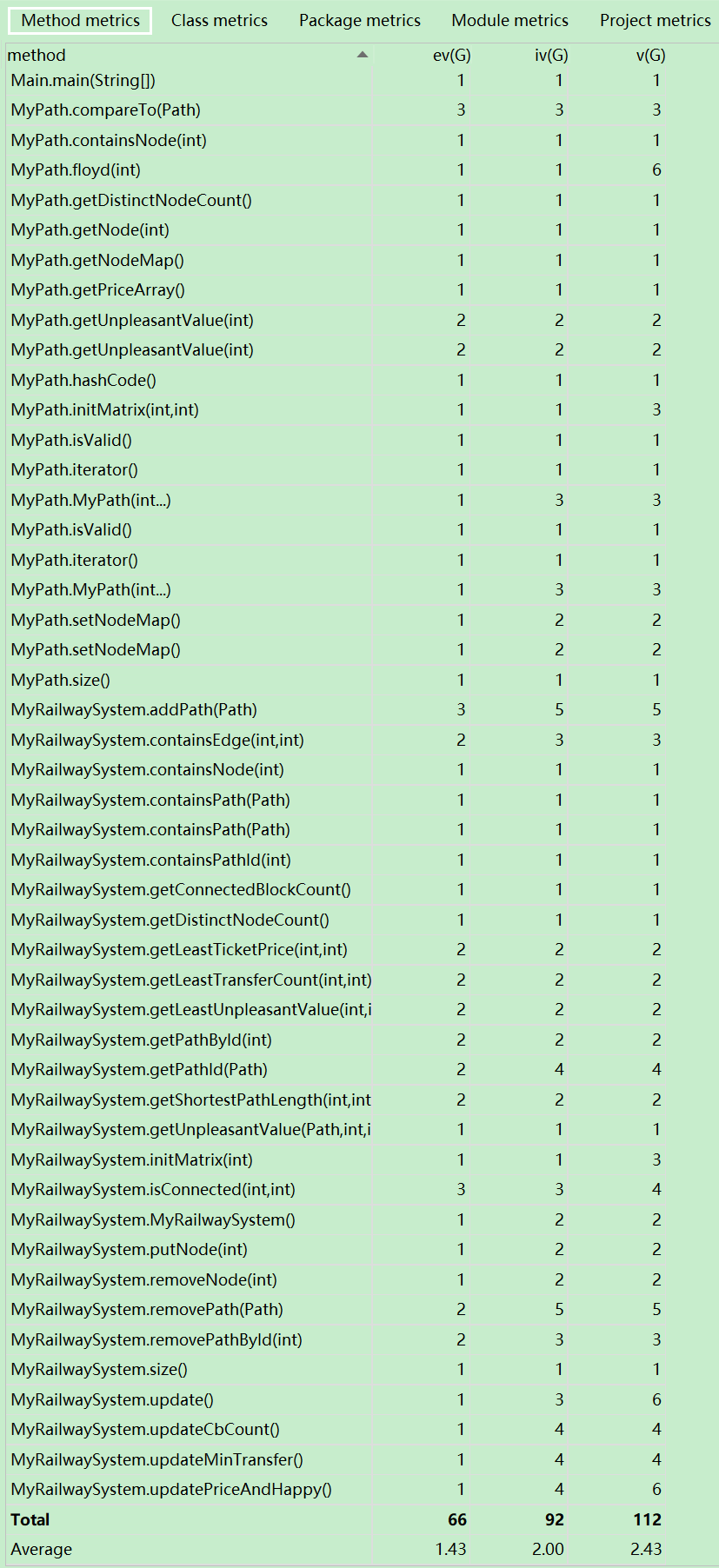
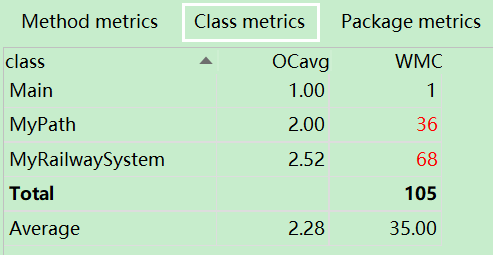
2）結構分析

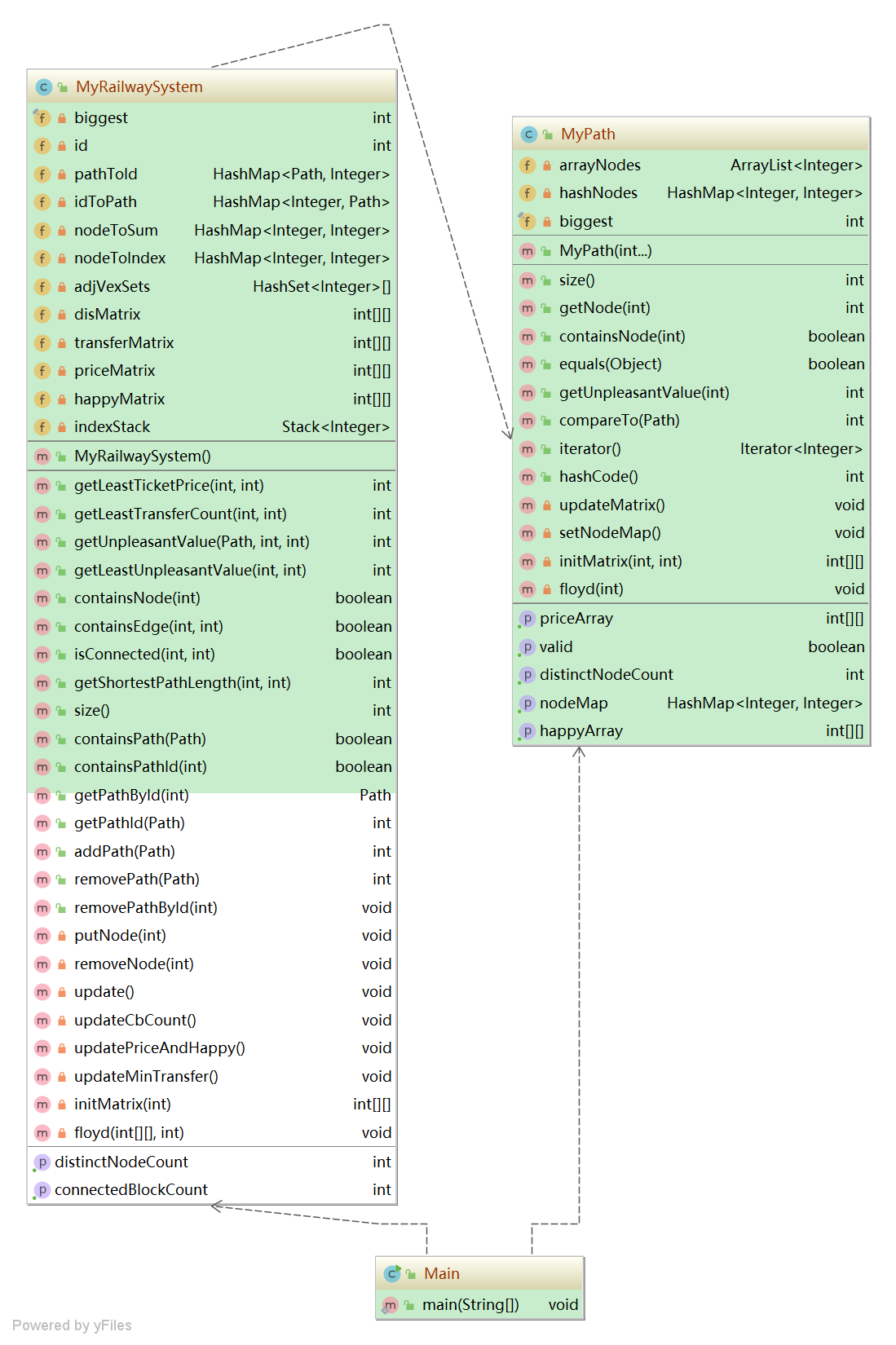
3）算法分析

• MyRailwaySystem

  • private int cbCount = 0; // 連通塊個數
    private int[][] disMatrix; // 距離矩陣 
    private int[][] transferMatrix; // 最小換乘矩陣
    private int[][] priceMatrix; // 價格矩陣
    private int[][] happyMatrix; // 最低不滿意度矩陣

  • // 下面是算法的偽代碼，以價格矩陣的更新為例，其它類似
    private void updatePriceMatrix() {priceMatrix = initMatrix(2);for (Each path : paths) {maxSize = path.size();priceArray = ((MyPath)path).getPriceArray();nodeMap = ((MyPath)path).getNodeMap();for (Each node1, node2 : nodeMap)if (priceArray[tempId1][tempId2] + 2 < priceMatrix[index1][index2]) priceMatrix[index1][index2] = priceMatrix[index2][index1] = priceArray[tempId2][tempId1] + 2;}floyd(priceMatrix, 125);
    }

4）迭代中對架構的重構

• MyPath

  • 在MyPath添加了兩個距離矩陣，用來存儲一個Path（地鐵線路）內部的（加權）距離信息。

  • 首先，將Path構建成兩個加權無向圖（權值分別為價格和滿意度）；然后，通過Floyd算法生成各自的距離矩陣，存儲下來。

  • private int[][] priceArray; // 加權（價錢）距離矩陣
    private int[][] happyArray; // 加權（滿意度）距離矩陣
    // 以下是算法的偽代碼
    private void updateMatrix() {setNodeMap(); // 重新建立映射關系priceArray = initMatrix(nodeCount, 2); // 距離矩陣初始化happyArray = initMatrix(nodeCount, 32); // 距離矩陣初始化for (Each node1, node2 ：nodes) { // 建圖賦權priceArray[node1.index][node2.index] = priceArray[node2.index][node1.index] = 1;happyArray[node1.index][node2.index] = happyArray[node2.index][node1.index] = = CalculatePleasure();}floyd(priceArray); floyd(happyArray); // 計算各點之間距離
    }

2. BUG分析

1）bug情況

• 這種算法在測試數據（最多結點數以及最多圖變動指令數）有所約束時，展現出非常出色的性能。在強測與互測中均未出現錯誤。
• 但是，我的代碼結構有著較為嚴重的問題：幾乎完全面向過程的寫法嚴重違反了OOP的原則；多個相似結構重復計算等。

2）修復情況

• 尚未進行代碼重構，僅對課程組給出的標程進行了研究，并進行了簡單的算法優化嘗試。

規格撰寫的心得與體會

• 規格化設計和契約式編程，讓人如沐清風，受益匪淺。 其實這次的代碼工程量很大，但是由于課程組給出的JML的引導以及課程組已經將我們需要填寫的代碼抽象成了接口，這使得我們在寫代碼時會產生一種錯覺——“這是面向對象課程嗎？”、“這是數據結構補習課吧！”…… 這正是規格化設計和契約式編程 的巨大作用。
• JML語言——好用不好寫。 JML語言書寫的困難度過高（從課程組編寫JML出現的各種狀況可以看出），給我的感覺是“可遠觀而不可褻玩”。而且，由于DDL過多加上學習資料不足（網上、課程資料都幾乎為零），我缺乏自己動手寫JML的動力。
• 沒有指引，路程變成了痛苦的過程。也許，是因為JML這一課還在探索階段，課程對JML編寫、檢測、使用的工具的講解和介紹頗少，基本全靠討論區和大佬們的指點，自己摸索著完成任務。固然，可以說這是對我們自主學習能力的養成，但是，有必要嗎？我相信JML單元會一步步從碎片化走向體系化，更加容易上手。
• 在路上 ……

最后，衷心感謝為這門課程辛苦付出的老師和助教。???