杭州集訓Day5

下面是Day5的題目！（其實都咕了好幾天了

100+70+40=210.

---

?

T1 皇后 XY 的疑難?_{(1s 512MB)}

1.1 題目描述

有一個n*n的王國城堡地圖上，皇后XY喜歡看騎士之間的戰斗，于是他準備布置m個騎士，其中

每一個騎士都可以向8個方向，上、下、左、右、左上、左下、右上、右下移動若干距離。且每一個騎士都可以攻擊他八個方向上離它最近的騎士。

皇后XY等不及看騎士之間的對決，但他又擔心騎士的安危，她想提前知道每一個騎士會被從幾個方向攻擊到，設為 s。很顯然 s 屬于[0,8] 。最后要求出來 num[0]，num[1] ……num[8] 九個數，表示有多少騎士被攻擊到0次，1次……8次。 數據保證m個騎士中任意兩個不在同一個位置。

1.2 輸入格式

第一行兩個正整數 n,m（n,m≤10⁵），然后接下來m行，每一行x[i]，y[i] 分別表示第i個騎士的

橫坐標和縱坐標。1≤x[i],y[i]≤n。

1.3 輸出格式

一行9個整數，分別為 num[0]，num[1]……num[8] ，兩個數中間用空格隔開。

1.4 樣例輸入

8 4
4 3
4 8
6 5
1 6

1.5 樣例輸出

0 3 0 1 0 0 0 0 0

1.6 數據約定

對于 30%的數據，n,m≤1000。

對于 60%的數據， n≤100000，m≤1000。

對于 100%的數據， n,m<=100000，1≤x[i],y[i]≤n?。

這不就是皇后的攻擊方式嗎

所以我們很容易想到“八皇后”那題的寫法

就是用四個數組分別存每行，每列，每個左斜線(x-y)，每個右斜線(x+y)的騎士個數

但是這題要求每個騎士八個方向上有沒有別的騎士

就不能只用四個數組了

要用八個數組存八個方向的最大值

比如說第i列的最上面的騎士和最下面的騎士的縱坐標

這樣的話在這一列的騎士的縱坐標如果大于最下面的就說明他不是最下面的

說明他下面還有人

如果其縱坐標小于最上面的就說明他不是最上面的

也就說明他上面還有人

然后注意下左斜線的x-y不能為負數，所以統一加個N即可（還要注意下數組大小

很簡單的一題，時間復雜度為O(n)

---

T2 快來 pick sxk_{(1s 512MB)}

2.1 題目描述
千古神犇邵徐坤 sxk，他現在利用自己猴子的屬相變成了n個會打籃球的分身，每個會打籃球的分身都
有一個雞兒你真美值，這些分身是亂序的。
你需要將其按雞兒你真美值從小到大排序，每次你可以將一個分身揪到任意一個位置（某兩個分身中
間），代價是你要掉該分身的雞兒你真美值的毛。
為了不變成sxk這樣的聰明"絕頂"的大猴子，你要以盡量少的代價完成這個任務，你需要回答每一次
分身后你會掉的最少毛數。
2.2 輸入格式
從文件pick.in中讀入數據。
數據的第1行包含一個非負整數t表示sxk分身的次數。
對于每一組數據
第1行包含一個非負整數n表示分身的個數
第2行包含n個數，a_i表示第i個分身的雞兒你真美值
2.3 輸出格式
輸出到文件pick.out中。
對于每一個詢問輸出一個整數，表示你最少會掉的毛數
2.4 樣例輸入

2

5

9?5 7 2 8

5

7?6 5 4 3?

2.5 樣例輸出

11

18
2.6 數據約定
對于30%的數據滿足 Σn≤1000.
對于另外30%的數據滿足 a_i>a_i+1.
對于100%的數據滿足 Σn≤200000，a_i≤10⁷.

很顯然每個數要移的話一次就夠了

這樣的話問題就被轉化成了

“刪除一些數，使得剩下的數剛好成不下降序列，要刪除的數總和盡量小”

即“求最大權值不下降子序列”

前30%的數據O(n²)dp就可以了（f[i]=max{f[j]}+a[i],j<i,a[j]<=a[i]）

a_i>a_i+1的30%數據很顯然答案就是a₂+a₃+...+a_n

接下來考慮100分做法

其實也不難，就是把dp優化成O(nlog n)的就行了，

把f[i]用權值線段樹維護一下，

查a[j]<=a[i]中f[j]的最大值還是很好求的

下面是代碼：

#include<bits/stdc++.h>
#define Lowbit(i) (i&(-i))
#define ll long long
using namespace std;
const int N=2e5+1e4;
int n,a[N],b[N],p[N*50]; ll w[N];
ll Max(ll x,ll y){return x>y?x:y;
}
int rd(){int s=0,ff=1;char w=getchar();while(w<'0'||w>'9'){if(w=='-') ff=-1;w=getchar();}while(w>='0'&&w<='9'){s=s*10+(w-'0');w=getchar();}return s*ff;
}
ll Query(int x){ ll maxn=0;for(int i=x;i;i-=Lowbit(i))maxn=Max(maxn,w[i]);return maxn;
}
void Add(int x,ll y){for(int i=x;i<=n;i+=Lowbit(i))w[i]=Max(w[i],y);
}
int main(){
//    freopen("pick.in","r",stdin);
//    freopen("pick.out","w",stdout);int t=rd();while(t--){ n=rd(); int fla=0; ll tot=0;for(int i=1;i<=n;i++)a[i]=rd(),b[i]=a[i],tot+=a[i];sort(b+1,b+1+n); int ct=0;for(int i=1;i<=n;i++){if(i==1||b[i]!=b[i-1]) ct++;p[b[i]]=ct;}ll maxn=-1e17;for(int i=1;i<=n;i++){ll f=Query(p[a[i]]); Add(p[a[i]],f+a[i]);
//            for(int j=1;j<i;j++)
//                if(a[j]<=a[i])
//                    f[i]=Max(f[i],f[j]+a[i]);maxn=Max(maxn,f+a[i]);}for(int i=1;i<=n;i++) p[a[i]]=0,w[i]=0;printf("%lld\n",tot-maxn); continue;}return 0;
}

對了，我訂正的時候用的是樹狀數組，

因為是求前綴的最大值，所以樹狀數組是可以的，

記住區間求最大值千萬不能用樹狀數組。

---

T3 一道另類的前綴和_{(1s 512MB)}

3.1 題目描述

已知常數 n，k ，p 和函數

?

你需要計算該函數的前綴和S(n)對p取模的結果

?

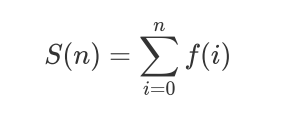
3.2 輸入格式

從文件prefix.in中讀入數據。

數據的第1行包含三個非負整數 n，k ，意義如題目描述。

3.3 輸出格式

輸出到文件prefix.out中。輸出一行一個正整數，S(n)可能為分數，所以輸出S(n)對p取模的結

果。

即S(n)=a/b輸出a*b^-1.

3.4 樣例輸入

5 2 998244353

3.5 樣例輸出

465847367

3.6 數據約定

對于100%的數據n≤10⁷，k≤10⁷，k≤n.

?

一道數論題，先推式子：

?

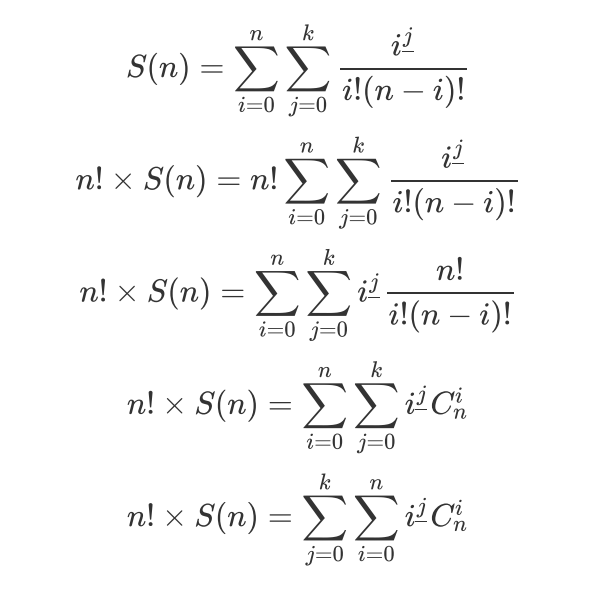
現在求出即可

?

前20%的n≤2000，預處理下，直接這樣模擬就行了

再來看k=0，由二項式定理得：

S(n)就可以算出來了

到這里你就可以獲得40分的好成績，當然還不夠，

要繼續的話，我得先引出一個推論：

?

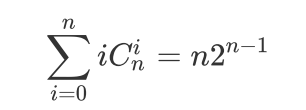
證明如下：

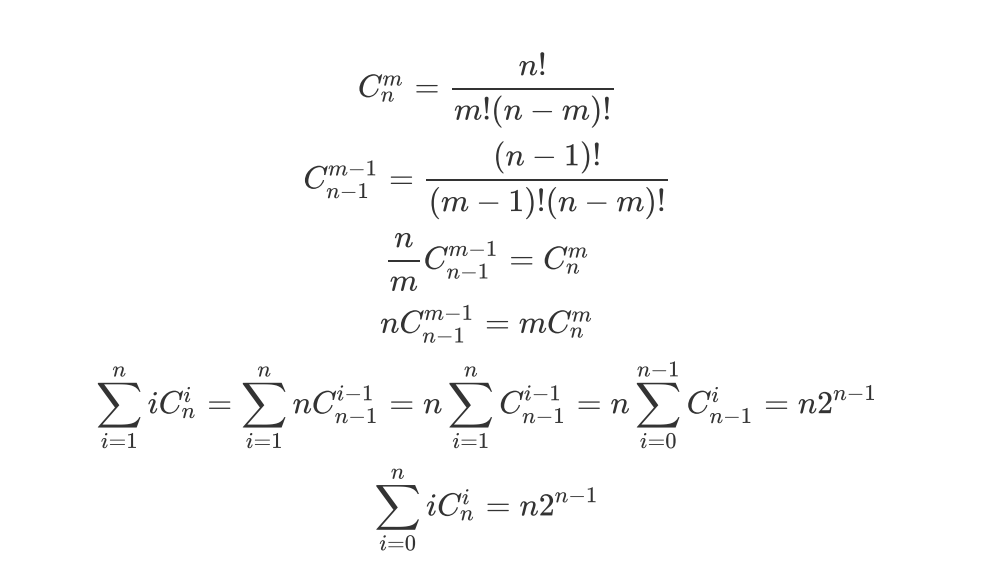
k=1就可以了

很簡單對吧，我們繼續

先模擬下k=2的情況

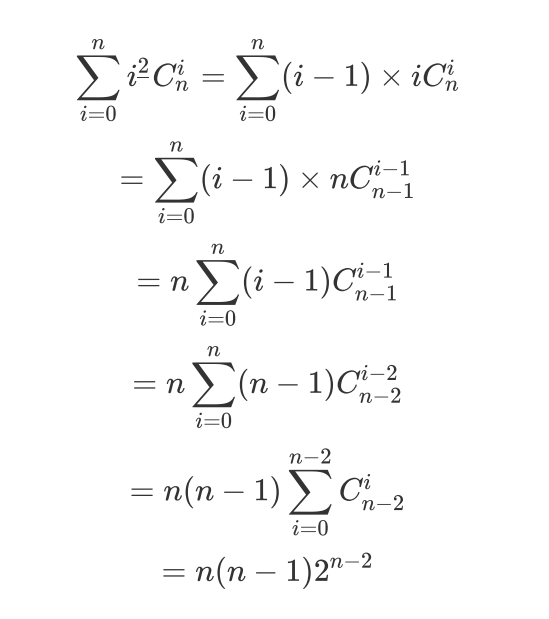
以此類推就可以得出最終答案：

?

就是

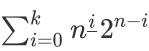
發現用到的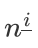只有k個，把它和2ⁱ滾動地處理出來，但需要求n！

所以時間復雜度為O(n)。

拜拜~