Java面試你必須要知道的那些知識，面試建議

二、面試題

面：考你幾個紅黑樹的知識點🦀

紅黑樹的數據結構都用在哪些場景，有什么好處？
紅黑樹的時間復雜度是多少？
紅黑樹中插入新的節點時怎么保持平衡？

面：2-3樹都是不沒看，回去等消息吧！

三、2-3樹與紅黑樹的等價性

紅黑樹規則

1. 根節點是黑色
2. 節點是紅黑或者黑色
3. 所有子葉節點都是黑色(葉子是NIL節點，默認沒有畫出來)
4. 每個紅色節點必須有兩個黑色子節點(也同樣說明一條鏈路上不能有鏈路的紅色節點)
5. 黑高，從任一節點到齊每個葉子節點，經過的路徑都包含相同數目的黑色節點

那么，這些規則是怎么總結定義出來的呢？接下里我們一步步分析講解。

1. 為什么既有2-3樹要有紅黑樹

首先2-3樹(讀法：二三樹)就是一個節點有1個或者2個元素，而實際上2-3樹轉紅黑樹是由概念模型2-3-4樹轉換而來的。-4叉就是一個節點里有3個元素，這在2-3樹中會被調整，但是在概念模型中是會被保留的。

雖然2-3-4樹也是具備2-3樹同樣的平衡樹的特性，但是如果直接把這樣的模型用代碼實現就會很麻煩，且效率不高，這里的復雜點包括；

2-叉、3-叉、4-叉，三種結構的節點類型，互相轉換復雜度較高
3-叉、4-叉，節點在數據比較上需要進行多次，不像2-叉節點，直接布爾類型比較即可非左即右
代碼實現上對每種差異，都需要有額外的代碼，規則不夠標準化

所以，希望找到一種平衡關系，既保持2-3樹平衡和O(logn)的特性，又能在代碼實現上更加方便，那么就誕生了紅黑樹。

2. 簡單2-3樹轉紅黑樹

2-3樹轉紅黑樹，也可以說紅黑樹是2-3樹和2-3-4樹的另外一種表現形式，也就是更利于編碼實現的形式。

簡單轉換示例；

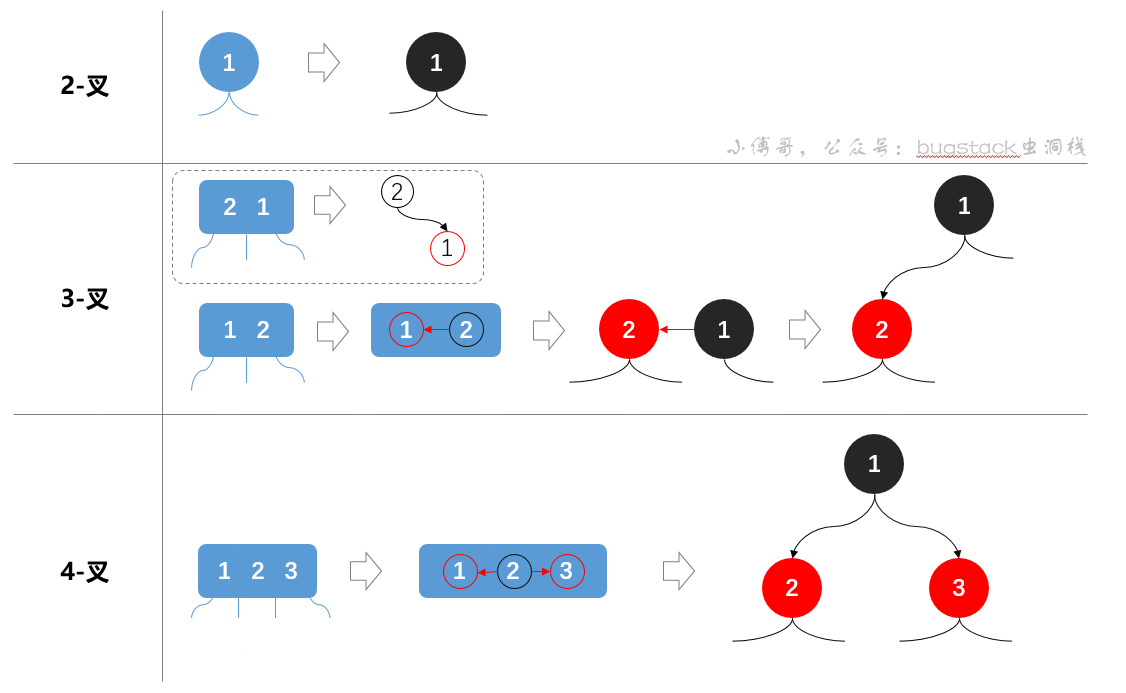
從上圖可以看出，2-3-4樹與紅黑樹的轉換關系，包括；

2-叉節點，轉換比較簡單，只是把原有節點轉換為黑色節點
3-叉節點，包括了2個元素，先用紅色線把兩個節點相連，之后拆分出來，最后調整高度黑色節點在上
4-叉節點，包括了3個元素，分別用紅黑線連接，之后拆分出來拉升高度。這個拉升過程和2-3樹調整一致，只是添加了顏色

綜上，就是2-3-4樹的節點轉換，總結出來的規則，如下；

將2-3-4樹，用二叉樹的形式表示
3-叉、4-叉節點，使用紅色、黑色連線進行連接
另外，3-叉節點有兩種情況，導致轉換成二叉樹，就有左傾和右傾

3. 復雜2-3樹轉紅黑樹

在簡單2-3樹轉換紅黑樹的過程中，了解到一個基本的轉換規則右旋定義，接下來我們在一個稍微復雜一點的2-3樹與紅黑樹的對應關系，如下圖；

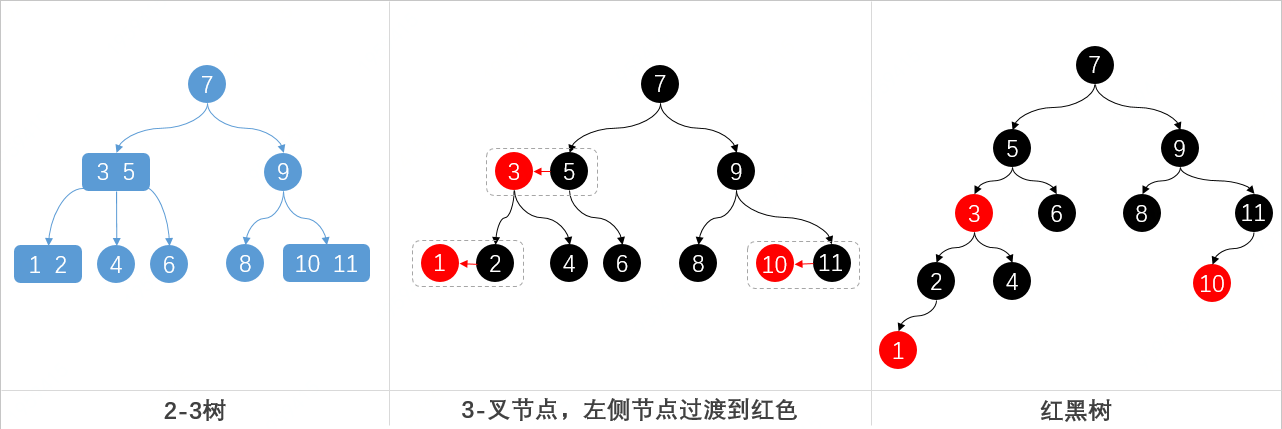
上圖是一個稍微復雜點的2-3樹，轉換為紅黑樹的過程，是不這樣一張圖讓你對紅黑樹更有感覺了，同時它也滿足一下條件；

從任意節點到葉子節點，所經過的黑色節點數目相同
黑色節點保持著整體的平衡性，也就是讓整個紅黑樹接近于O(logn)時間復雜度
其他紅黑樹的特點也都滿足，可以對照紅黑樹的特性進行比對

四、紅黑樹

1. 平衡操作

通過在上一章節2-3樹的學習，在插入節點時并不會插到空位置，而是與現有節點融合以及調整，保持整個樹的平衡。

而紅黑樹是2-3-4樹的一種概念模型轉換而來，在插入節點時通過紅色鏈接相連，也就是插入紅色節點。插入完成后進行調整，以保持樹接近平衡。

那么，為了讓紅黑樹達到平衡狀態，主要包括染色、?左右旋轉、這些做法其實都是從2-3樹演化過來的。接下來我們就分別講解幾種規則的演化過程，以此更好了解紅黑樹的平衡操作。

1.1 左旋轉

左旋定義： 把一個向右傾斜的紅節點鏈接(2-3樹，3-叉雙元素節點)，轉化為左鏈接。

背景：順序插入元素，1、2、3，2-3樹保持平衡，紅黑樹暫時處于右傾斜。

接下來我們分別對比兩種樹結構的平衡操作；

2-3樹，所有插入的節點都會保持在一個節點上，之后通過調整節點位置，保持平衡。
紅黑樹，則需要通過節點的左側旋轉，將元素2拉起來，元素1和元素3，分別成為左右子節點。

紅黑樹的左旋，只會處理與之對應的2-3樹節點進行操作，不會整體改變。

1.2 右旋轉

右旋定義： 把一個向左傾斜的紅節點連接(2-3樹，3-叉雙元素節點)，轉換為右連接。

背景：順序插入元素，3、1、1，2-3樹保持平衡，紅黑樹暫時處于左傾斜。

接下來我們分別對比兩種樹結構的平衡操作；

2-3樹，所有插入的節點都會保持在一個節點上，之后通過調整節點位置，保持平衡。
紅黑樹，則需要通過節點的右側旋轉，將元素2拉起來，元素1和元素3，分別成為左右子節點。

你會發現，左旋與右旋是相互對應的，但在2-3樹中是保持不變的

1.3 左右旋綜合運用

左旋、右旋，我們已經有了一個基本的概念，那么接下來我們再看一個可以綜合左右旋以及對應2-3樹的演化案例，如下；

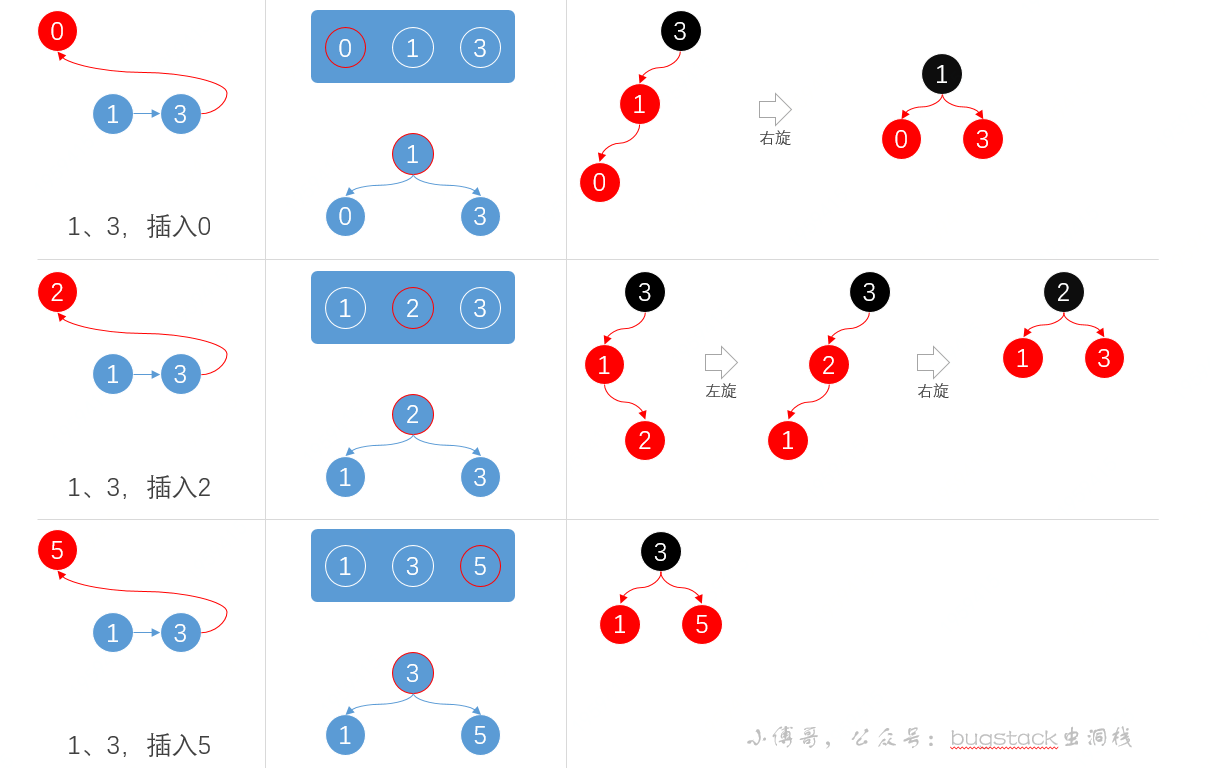
以上的例子分別演示了一個元素插入的三種情況，如下；

1、3，插入0，左側底部插入，與2-3樹相比，需要右旋保持平衡
1、3，插入2，中間位置插入，首先進行左旋調整元素位置，之后進行右旋進行樹平衡
1、3，插入5，右側位置插入，此時正好保持樹平衡，不需要調整

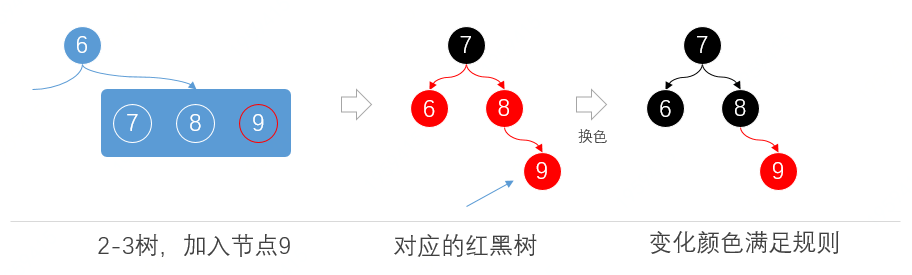
1.4 染色

在2-3樹中，插入一個節點，為了保持樹平衡是不插入到空位置上的，當插入節點后元素數量有3個后則需要調整中間元素向上，來保持樹平衡。與之對應的紅黑樹則需要調整顏色，來保證紅黑樹的平衡規則，具體參考如下；

2. 旋轉+染色運用案例

接下來我們把上面講解到的旋轉、染色，運用到一個實際案例中，如下圖；

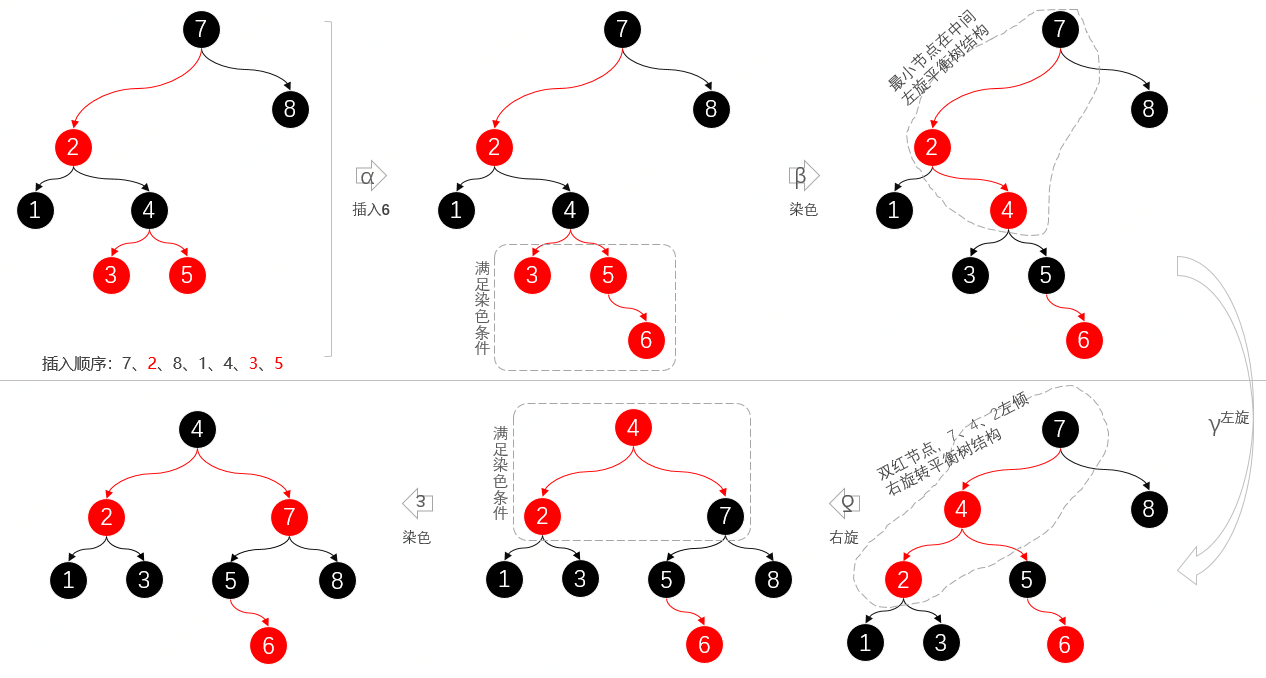
首先從左側開始，是一個按照順序插入生產出來的紅黑樹，插入順序；7、2、8、1、4、3、5
α，向目前紅黑樹插入元素6，插入后右下角有三個紅色節點；3、5、6。
β，因為右下角滿足染色條件，變換后；黑色節點(3、5)、紅色節點(4、6)。
γ，之后看被紅色連線鏈接的節點7、4、2，最小節點在中間，左旋平衡樹結構。
δ，左旋完成后，紅色鏈接線的7、4、2為做傾順序節點，因此需要做右旋操作。
ε，左旋、右旋，調整完成后，又滿足了染色操作。到此恢復紅黑樹平衡。

注意，所有連接紅色節點的，都是是紅色線。以此與2-3樹做對應。

3. 刪除操作

根據2-3-4樹模型的紅黑樹，在刪除的時候基本是按照2-3方式進行刪除，只不過在這個過程中需要染色和旋轉操作，以保持樹平衡。刪除過程主要可以分為如圖四種情況，如下；

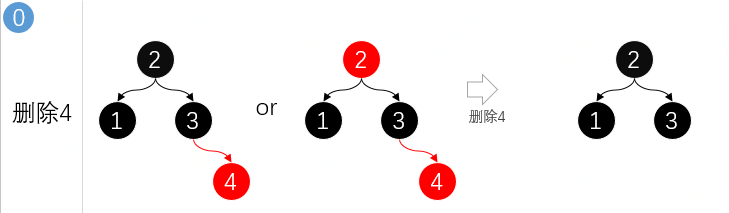
3.1 刪除子葉紅色節點

紅色子葉節點的刪除并不會破壞樹平衡，也不影響樹高，所以直接刪除即可，如下；

3.2 刪除左側節點

3.2.1 被刪節點兄弟為黑色&含右子節點

3.2.2 被刪節點兄弟為黑色&含左子節點

3.2.3 被刪節點兄弟為黑色&含雙子節點(紅)

3.2.4 被刪節點兄弟為黑色&不含子節點

3.2.5 被刪節點兄弟為黑色&含雙黑節點(黑)

3.3. 刪除右側節點

3.3.1 被刪節點兄弟為黑色&含左子節點

3.3.2 被刪節點兄弟為黑色&含右子節點

3.3.3 被刪節點兄弟為黑色&含雙子節點(紅)

3.2.4 被刪節點兄弟為黑色&不含子節點

3.2.5 被刪節點兄弟為黑色&含雙黑節點(黑)

最后

即使是面試跳槽，那也是一個學習的過程。只有全面的復習，才能讓我們更好的充實自己，武裝自己，為自己的面試之路不再坎坷！今天就給大家分享一個Github上全面的Java面試題大全，就是這份面試大全助我拿下大廠Offer，月薪提至30K！

資料領取方式：藍色傳送門

我也是第一時間分享出來給大家，希望可以幫助大家都能去往自己心儀的大廠！為金三銀四做準備！
一共有20個知識點專題，分別是：