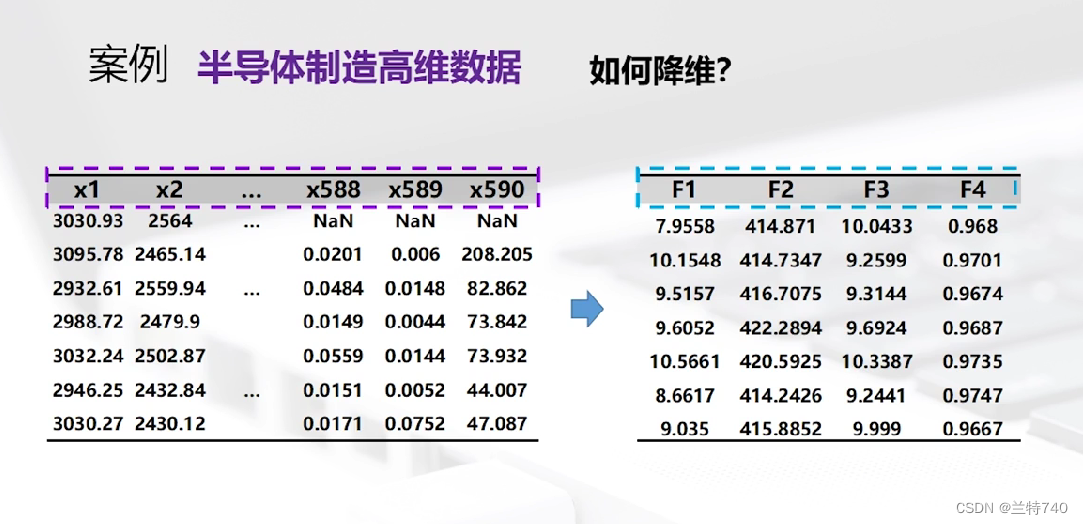
數據降維不只存在于半導體數據中，它是存在于各行各業的，我們要分析的數據維數較多的時候全部輸入維數較大這時就要采取降維的方法綜合出主要的幾列用于我們的分析。


PCA的哲學理念是要抓住問題的主要矛盾進行分析，是將多指標轉化為少數幾個綜合指標進行分析。


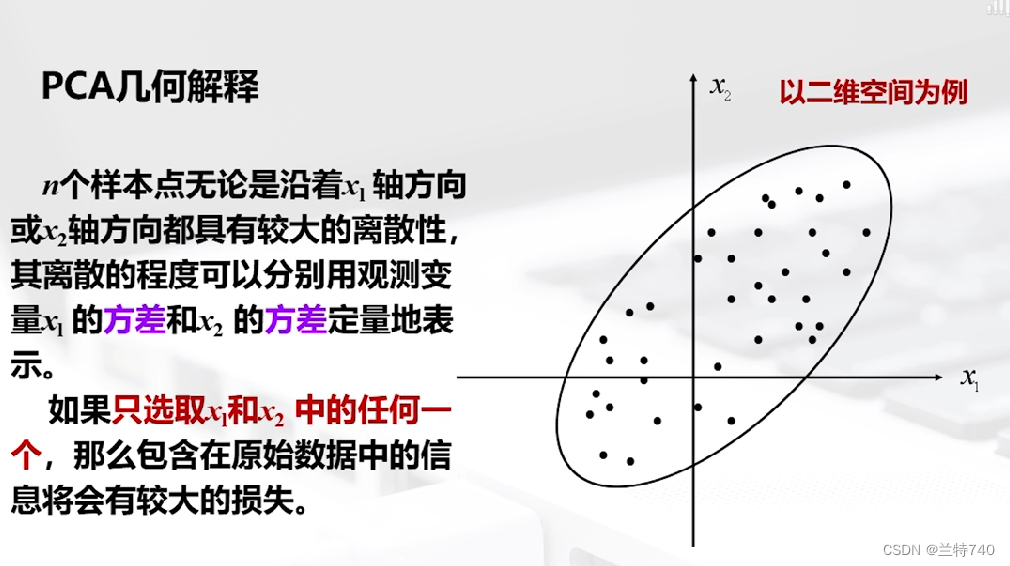
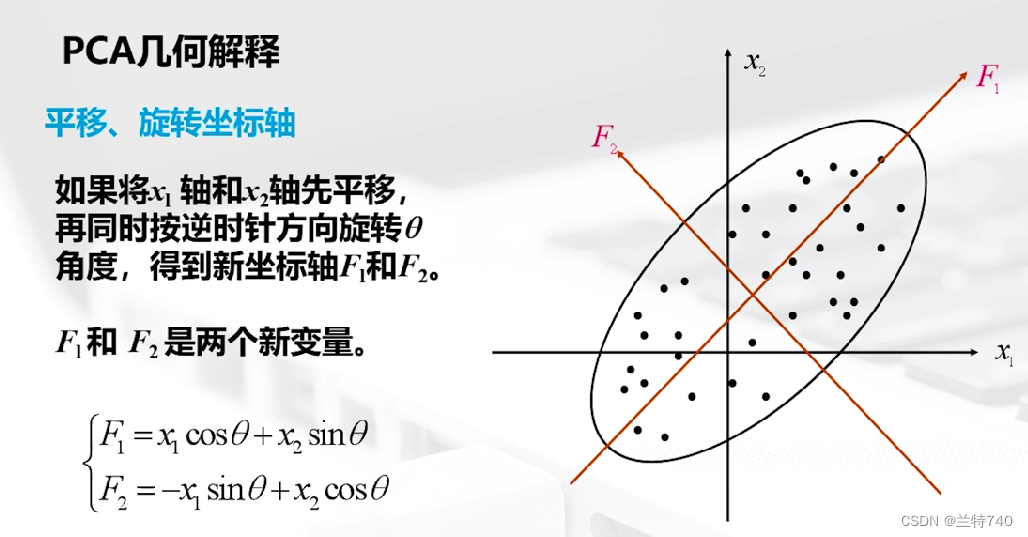
以二維空間為例的話 n 個樣本點無論是沿著X1軸方向或者X2軸方向都有很大的離散型，因為我們看到此時二維空間中的這個形狀是橢圓形的，如果只選取X1和X2中的任何一個那么包含在原始數據中的信息都會有較大的損失，如果將X1軸和X2軸先平移，再同時按逆時針方向旋轉一定角度，便會得到新坐標軸。

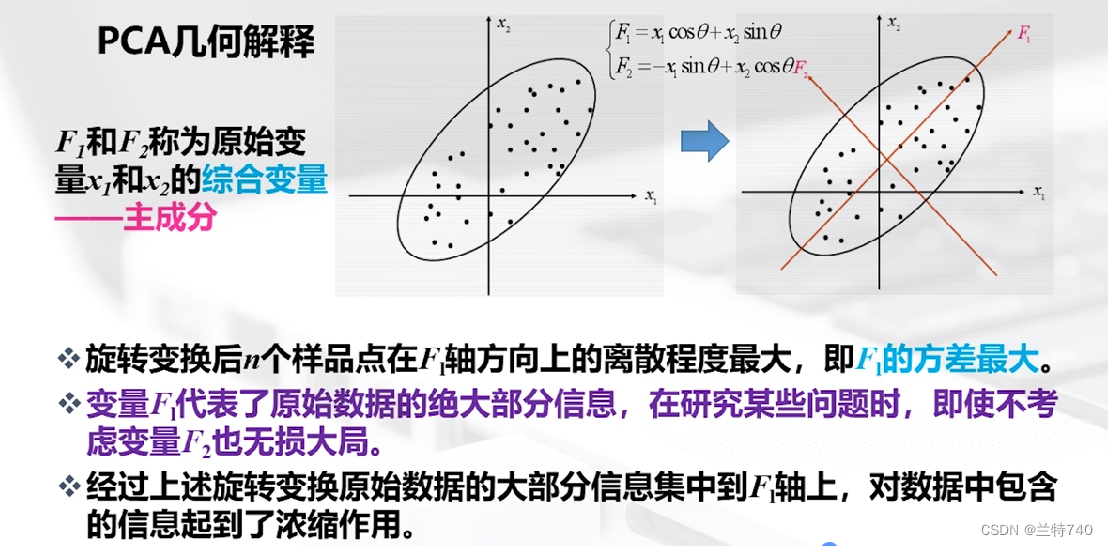
得到的新的坐標軸F1和F2稱為原始變量X1和X2的綜合變量，旋轉變換后n個樣品在F1軸方向上的離散程度最大，即F1的方差最大，變量F1代表了原始數據的絕大部分信息，在研究某些問題時，即使不考慮F2也無損大局。

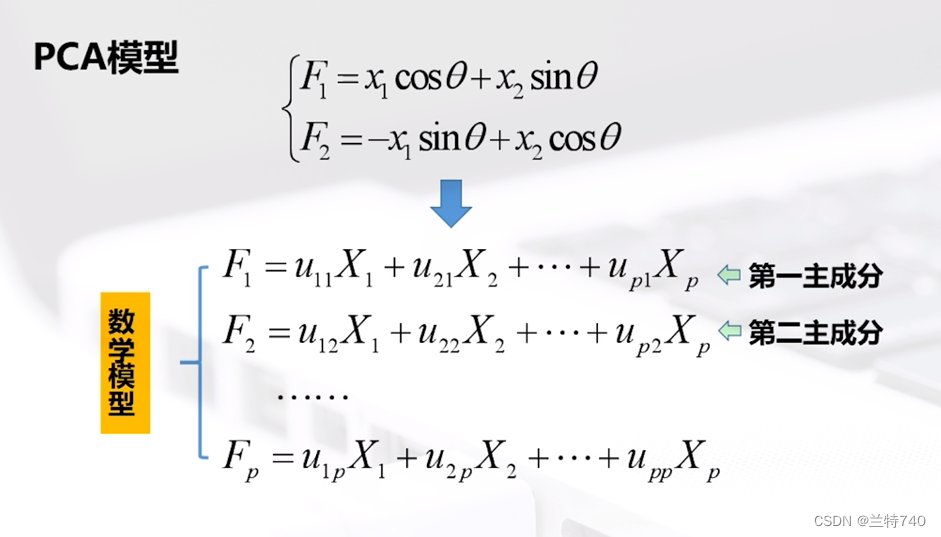
以二維模型為例，經過變換后的F1和F2的方向如圖所示，同時我們可以擴展到多維模型，假如X是P維模型為例，我們會依次找出第一主成分和第二主成分等，但是找到的主成分的數量必然是遠遠小于P的。

求解之后我們可以得到各特征根對應的特征向量，其中最大特征根的特征向量對應第一主成分的的系數向量；第二大特征根的特征向量是第二大主成分的系數向量，雖然我們知道最后要使用的主成分的數量是遠遠小于初始的數量，那么最終應該選擇幾個主成分就是由方差累計貢獻率決定，我們要求的方差累計貢獻率越高，最終需要的主成分個數相應也越多。

'''step1 調用包'''
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
'''step2 導入數據'''
data=pd.DataFrame(pd.read_excel('data_secom.xlsx'))
'''step3 數據預處理'''
# 查看各列缺失情況
data.isnull().sum()
#缺失值填充
datanew = data.fillna('0')
#數據標準化，消除特征量綱的影響
#將屬性縮放到一個指定范圍,即(x-min)/(max-min)
scaler = MinMaxScaler()
scale_data = pd.DataFrame(scaler.fit_transform(datanew))
'''step4 PCA降維'''
#選擇保留85%以上的信息時，自動保留主成分
pca = PCA(0.85)
data_pca = pca.fit_transform(scale_data) #data_pca就是降維后的數據
data_pca_new = pd.DataFrame(data_pca)
print("保留主成分個數為：",pca.n_components_) #顯示保留主成分個數
#選取前兩主成分作圖
plt.scatter(data_pca[:,0], data_pca[:,1])
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()

一、調用必要的包

'''step1 調用包'''
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

此時需要注意的是看PCA是從哪調用的
二、導入數據

data=pd.DataFrame(pd.read_excel('data_secom.xlsx'))

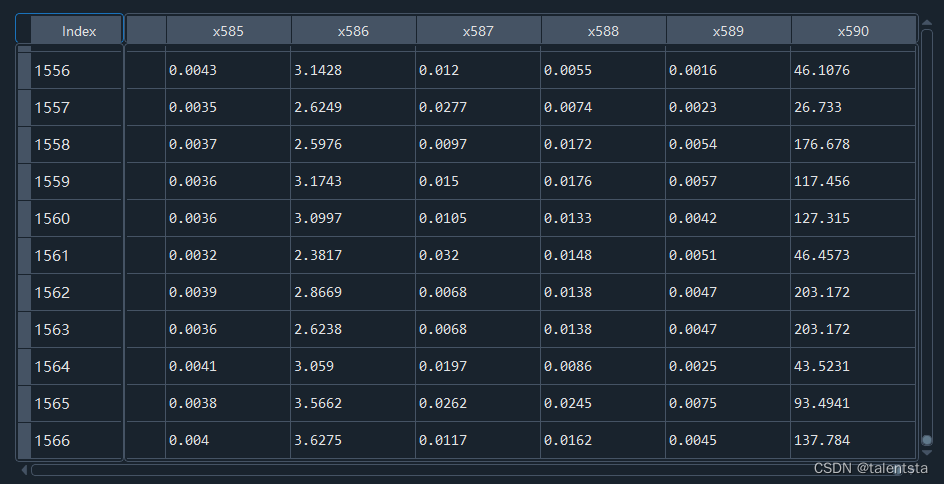
此時我們可以看到我們讀入的數據的行數和列數是非常大的。
三、數據預處理

'''step3 數據預處理'''
# 查看各列缺失情況
data.isnull().sum()
#缺失值填充
datanew = data.fillna('0')
#數據標準化，消除特征量綱的影響
#將屬性縮放到一個指定范圍,即(x-min)/(max-min)
scaler = MinMaxScaler()
scale_data = pd.DataFrame(scaler.fit_transform(datanew))

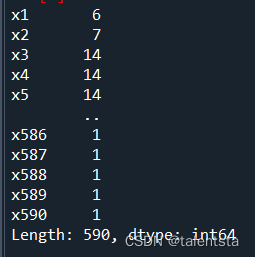
查看各列的缺失值情況后用 0 進行填充，同時再將屬性進行標準化從而縮放到一個指定范圍。

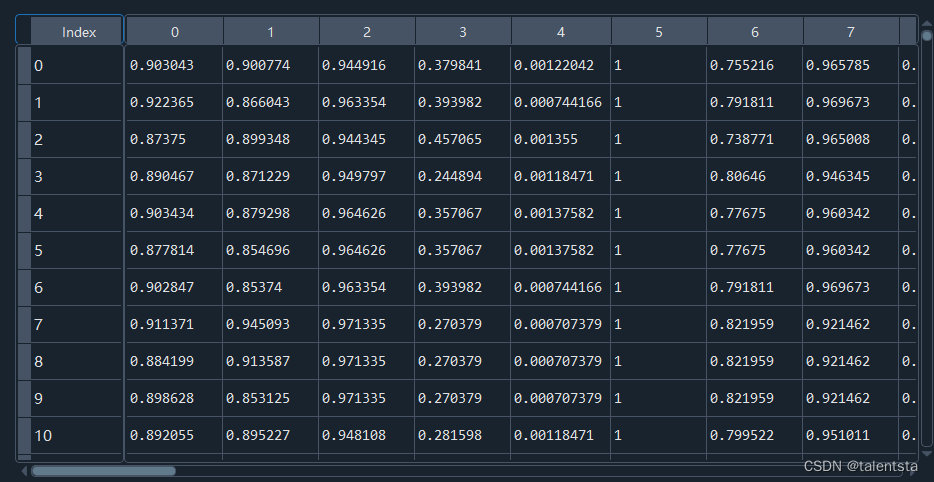
標準化后的數據如圖所示
四、PCA降維

'''step4 PCA降維'''
#選擇保留85%以上的信息時，自動保留主成分
pca = PCA(0.85)
data_pca = pca.fit_transform(scale_data) #data_pca就是降維后的數據
data_pca_new = pd.DataFrame(data_pca)
print("保留主成分個數為：",pca.n_components_) #顯示保留主成分個數

這里我們可以看到選取不同的方差貢獻率之后，需要保留的主成分個數是不同的，
這段代碼使用PCA(Principal Component Analysis)對數據進行了降維處理。
具體步驟:

1. 創建PCA對象pca,設置降維比例為0.95。
2. 調用PCA對象的fit_transform()方法,輸入歸一化后的數據scale_data。
3. fit_transform()先擬合數據,找到主成分方向,然后進行降維轉換。
4. 其中參數0.95表示保留95%的信息量進行降維。
5. 返回的data_pca就是降維處理后的結果數據。
6. 將其轉換為DataFrame格式,存儲在data_pca_new中。
   這樣就可以利用PCA對高維數據進行預處理,去除冗余信息,降低維度,減少特征間相關性。
   降維比例需要根據實際情況來設置,一般0.9-0.99之間。保留越多信息,降維效果越小。
   PCA降維是機器學習中常用的一種維數約簡方法,可以有效簡化模型,防止過擬合。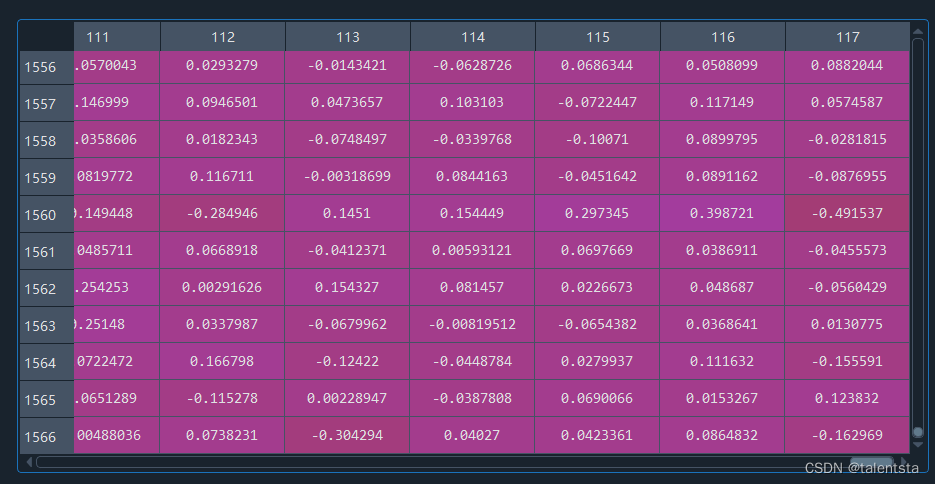
   大家此時可以看到降維后的數據現在是有118列，行數是沒有變化的。

#選取前兩主成分作圖
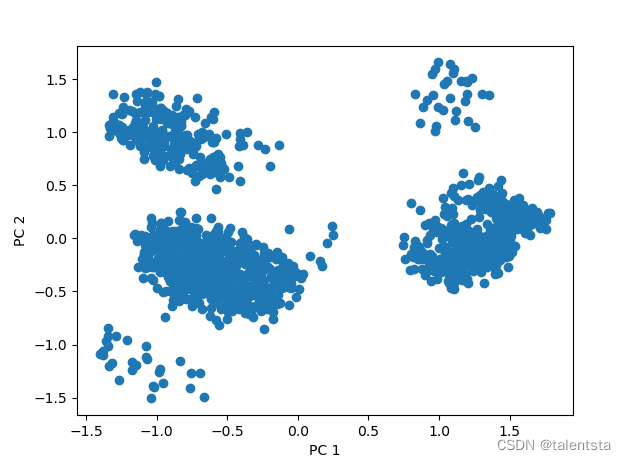
plt.scatter(data_pca[:,0], data_pca[:,1])
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.show()

最后再選取前兩個主成分作圖進行可視化分析。