0 前言
0.1 討論層級和范圍
- 討論層級
- 計算機底層:硬件層次與匯編指令層次
- 信息與二進制位
- 討論范圍
- 信息的存儲與運算在匯編語言與Verilog HDL中的聯系與區別
- 事實上,數據越界截斷問題,在計算機體系的任何層次,都可能發生,并且他們遵循的法則基本是一致的
0.2 其他說明
- 信息與數據,本質上來講沒有區別,信息就是數據,數據就是信息。為方便起見,在本文中,全部都稱數據。
- 數據越界問題的分析,在實際應用中有以下用途
- 在一開始設計的時候避免越界問題的發生
- 在發生錯誤的時候有能力分析出其原因
1 一個概念
越界丟失法則:超過存儲能力的數據,會被截斷,從而導致丟失,也可以稱為越界截斷。
這就好比,一個水桶一旦裝滿水,再灌水會溢出來,溢出的水就是丟失了
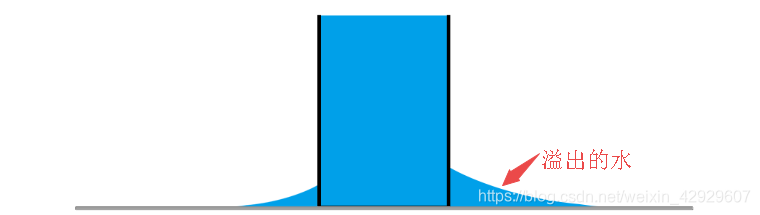
1.1 越界截斷
我們知道,數據在計算機中是以二進制信息存儲的,即一串一串的二進制數
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| … |
對于上圖所示的,是兩個8位的二進制位串。
下面將通過演示說明,什么是越界截斷,對于8個二進制位來說,所能表示的最大數據就是8位全部是1:
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|
如果再給這個數值加1,那么就會數值就變成:
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
這是9位二進制數,但實際上計算機只能存儲8位,因此超過其所能承受的范圍,最高位的1將會被截斷,從而造成數據丟失:
| 被截斷 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
也就變成了:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
這就是數據的越界截斷。
有些讀者可能會誤以為越界丟失就是歸零,因此我再舉一個例子,以消除誤解。
對于8個二進制位來說,如果給他施加了達到10個二進制位的數字:
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
那么它的最高兩位將會丟失
| 被截斷 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
也就變成了:
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
1.2 越界截斷建模——水溢出模型
數據的越界丟失,就好比水桶滿了,多出的水會溢出,但是水桶的水并不會消失,只是多出來的水丟失了。

1.3 補充概念——溢出
當數據發生越界,超出了容器容納范圍時,我們稱發生了溢出
2 兩個方向
對于越界截斷現象,有兩個考慮的方向。
2.1 數據的存儲——水桶儲水模型
信息的存儲是指,將信息直接存儲起來
就好比將水放進水桶中
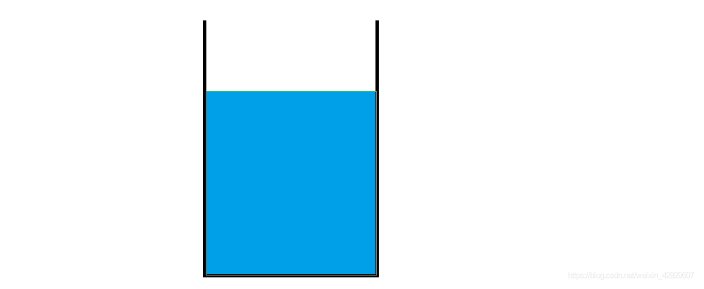
2.2 數據的運算——水處理模型
信息的運算是指,對傳輸過來的數據,進行運算(加、減、乘、除……),也就是數據的處理過程
就好比污水經過處理廠變成了凈水
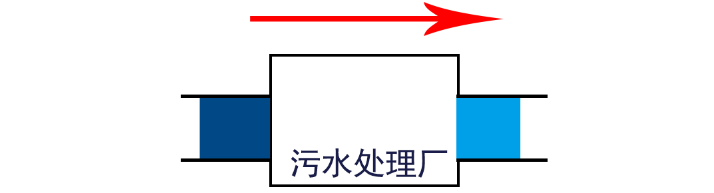
亦或者是一桶水倒入另外一桶水中,這樣的模型都是合理的,能夠幫助你理解這一過程
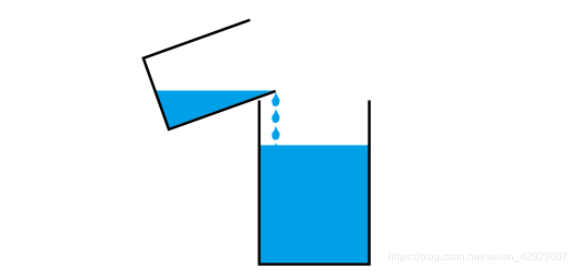
3 三個過程
對于越界截斷現象,一般會發生在三個過程中。
3.1 初始量:設初值
包含數據類型、標識符的設定,以及賦初值的過程
3.1.1 Verilog
在Verilog語言中,初始化的方式如下
reg a = 1'b1;
reg b = 123;
reg c;
c = 1'b0;
- 對于a和c來說,一個二進制位存儲一個二進制數,這是標準的
- 對于b來說,顯然數據越界了,Verilog會執行越界丟失操作,留下沒越界的數字
- 123用二進制表示是:0111_1011
- 因此留下最后一位1,其余高位全部丟失
3.1.2 匯編語言
以8086CPU中16位寄存器AX為例,說明數據的初始化問題
mov AX,11H // ①
mov AX,1000001H // ②
- 對于①,將它顯然正確
- 對于②,明顯越界,這是錯誤的指令,注意,是錯誤,可能不會被容錯直接報錯
3.1.3 C/C++等高級語言
int a = 1000100010000;
int b = 100;
- 很明顯,a越界了,b是正確的
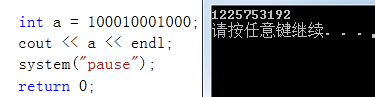
越界是錯誤的!
問題:為什么會顯示右側這一串數字?C++是怎么運行出來的?
在回答這個問題之前,先來學習一下延展知識。
3.1.3.1 延展閱讀1:VS C++ 的內存查看方法
【VS C++ 2010】查看內存的方法詳解
學習完之后,再繼續往下進行
以下面的代碼為示例:
int main()
{int a = 100;int b = 100010001000;cout << "a = " << a << " " << &a << endl;cout << "b = " << b << " " << &b << endl;system("pause");return 0;
}
以下,我們都需要使用剛剛學到的知識,查看內存的情況
(1)對于正數
①不越界的正數
對于int a = 100;,顯然是不越界的,其內存情況為
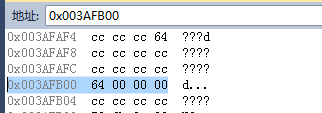
這一點沒什么好說的
- a的類型為int
- 數值為100(十進制),被解釋為數字100
- 存儲為二進制位串
- 顯示為0x64(十六進制的64)

②越界的正數
對于十進制數據 1000_1000_1000,其十六進制為:17 49 0F 82 68
| 17 | 49 | 0F | 82 | 68 |
|---|
由越界截斷可得,被保留下來的為:49 0F 82 68
| 被截斷 | 49 | 0F | 82 | 68 |
|---|
我們查看內存來驗證一下
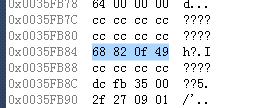
內存上的存儲的確是這樣,將其換算為十進制,就是我們的輸出結果了
(2)對于負數的越界
3.1.3.2 延展閱讀2:補碼的使用
補碼轉換人工求法【非常沒必要,計算機要做的事情為什么要人來做?不過做考試題還是有必要的……】:
- 求負數絕對值的原碼后減一【這個減一就很蠢,補碼的使用就是為了避免減法,你居然用減法來避免減法……,但是做考試題確實比用反碼的方法更快】
- 對上述結果全部取反
對于負數,計算機以補碼形式來存儲的本質
對于負數:
- 計算機先將其轉換為補碼形式
- 再進行存儲,如果越界,則會發送越界截斷
①不越界的負數
直接以補碼形式存儲
②越界的負數
先存儲為補碼,然后越界截斷,然后再存儲起來
3.1.4 小結
我通過三種語言的描述,來為你傳到這樣的信號:
- 不同語言對于越界問題的處理方式是不同的,這是顯而易見的,他們所處的計算機系統層次不一樣,抽象程度也不一樣
- 毫無疑問,在賦初值的時候就造成越界,這是設計的失敗,這是不可容忍的錯誤
總之,不要越界(后面的小節會講解它也是雙刃劍,可以**“變廢為寶”**)
3.1.4.1 延展閱讀3:在邊界內做事情
待完善部分,敬請期待
3.1.4.2 優化模型——水桶的水不能溢出
對于水桶儲水模型,請回看2.1節的內容,這里通過幾張圖來展示幾種可能的情況

3.1.4.3 一句話總結:做事不能越界
3.2 過程量:做運算
對于運算之后造成的越界問題,參考3.1.3節中的問題部分的解答即可
3.2.1 數學運算(加減乘除……)
不管是高級語言,還是匯編語言,在進行數學運算的時候都可能產生越界的問題——兩個數字都沒有越界,但是相加之后越界了
設計者一定要考慮并且避免這些問題的發生,否則可能會引發錯誤。
3.2.2 數據類型的強制轉換
3.2.2.1 手動強制轉換
數據的強制轉換也可能引發錯誤,比如:在java中,將int類型的數字轉換為byte類型,由高向低轉換,就可能引起數據的丟失。
例如下列Java代碼
int a = 300;
byte b = (byte)a;
System.out.println(b);
輸出為:

原因分析:
對于原數字,被保存為0x12C(十六進制前綴為“0x”),強制轉換為byte類型,則會發生越界截斷,將最高位的1截斷,變成了0x2C,也就是十進制的44
3.2.2.2 自動強制轉換
另外,在C/C++、Java中,有一類二元運算符,比如
- +=
- -=
- *=
- /=
例如x += y,它的本質是x = x + y,由于y的數據類型并不確定,因此可能會產生錯誤,比如:
int x = 3;
x = x + 3.5;
這是不被允許的,x + 3.5是float類型,不能直接賦值給int類型,這時候需要進行強制轉換x = (int)(x + 3.5),得到的結果是6
對于上述二元運算符來說,這個強制轉換是自動進行的
int x = 20;
x += 3.5;
對于第二條語句,并不等價于x = x + 3.5而是等價于x = (int)(x + 3.5)
3.3 結束量:得結果
3.3.1 直接輸出
對于得到的結果,直接輸出,那么就是越界丟失之后的結果,沒什么好說的。
如果直接在輸出函數的參數內進行運算,那么越界與否取決于實際的環境,看情況而定,數據的結果一定要在范圍內!。
3.3.2 結果被保存到其他變量中
如果運算得到的結果被保存到了其他變量中,如果將大的數據,保存到小容器中,顯然會越界
4 雙刃劍——越界截斷的利弊分析
4.1 避開弊端
從專業詞語來說,越界丟失更適合稱為越界截斷,越界的部分將會被計算機截斷,從而造成了丟失。

毫無疑問,數據的丟失是可怕的,因此,大多數情況下,尤其是程序員,要盡可能的避免發生越界截斷。
4.2 壞事變好:應用越界截斷——補碼的使用
從哲學的角度來說,任何事情都有兩面性,如果我們利用好越界截斷,也能讓它發揮巨大的作用。
計算機有加法器,但是它不擅長減法,于是
- 補碼+越界截斷
就完成了減法轉換為加法這一壯舉!
例如:45 + (-22) = 23
在計算機中,以補碼形式存儲,用補碼進行加減
45的補碼:
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
|---|
-22的補碼:
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
補碼相加:
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
|---|
發生越界截斷:
| 被截斷 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
|---|
得到:
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
|---|
也就是23的補碼
**但是,務必注意:**使用補碼進行運算,運算結果也一定要在范圍內,否則依然是錯誤。
5 注意事項:先確定正確的界限,才能分析越界截斷
比如下面這個例子,如果你把它的界限弄錯,那么你可能會得到錯誤的結果。
char a = 100;
char b = 28;
char c = a+b;
cout << dec << (int)c << endl;unsigned char d = a+b;
cout << dec << (int)d << endl;
會輸出
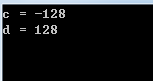
顯然,a+b并不會越界
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
但是,同樣是char類型,一個是有符號數,一個是無符號數,輸出的結果卻不一樣。
這是因為
- 對于有符號數來說,它的界限的7位,因為要除去符號位
- 對于無符號數來說,它的界限是8位,不需要除去符號位
說到這里,你也就明白,數據的界限是討論越界截斷的前提。
因此設計者要綜合考慮很多問題,這也是計算機科學家的基本素養。
6 綜合闡述
- 任何計算機程序都是由各種數據構成的
- 各種數據又擁有不同的數據類型
因此:數據只要在對應數據類型的范圍內,就不會發生錯誤。
最終結果就是,保證數據在數據類型的范圍內運行即可,對于補碼運算而言,中間過程發生越界是沒有問題的,但是結果不能越界,上面一大堆分析完全可以不用看(不要打我……分析有助于你未來思考更深入的問題,光記住結論是走不遠的)。
7 延展閱讀匯總
待補充
)

)

, ntohl() , htons(), htonl(), inet_ntoa(), inet_pton(), atoi()匯總)

)







:RadASM的安裝和使用說明)
)



