【題目描述】
CodeForces - 786BLegacy
【題目分析】
題目大概意思就是有三種操作:
- 從某個點到另一個點
- 從某個點到另一個區間
- 從某個區間到另一個點
然后詢問從其中一個點到其他所有點的距離——這很顯然是一個求單源最短路徑的。我們簡單的想法顯然是建一個圖,每次操作就進行暴力連邊,反正也沒有修改。可是復雜度不允許。
我們再觀察一下操作:對區間的操作,這讓我們不由得想起了線段樹,畢竟線段樹可是區間神器,可是就算用了線段樹,我們能做些什么呢?
線段樹是保存區間信息的數據結構,我們對于從點到區間的關系,不妨修改為從點到線段樹節點的關系,然后再使線段樹節點和他們的葉子節點之間本來就帶有一條路徑,那么從一個點到另一個區間的關系就這樣被簡化為從一個點到幾個點的關系,可以有效降低復雜度。
具體做法就是在建樹的過程中就讓每個線段樹節點和他們的葉子節點之間含有一條權值為0的有向邊。
之所以是有向邊是因為從點到區間的關系有兩種,我們得建立兩種線段樹,分別是從父節點指向葉子節點和從葉子結點指向根節點,對應的是從點到區間和從區間到點的關系。而且兩個線段樹的葉子節點,也就是最下面的節點指向的都是原來區間的節點,這樣就在原來的區間上建立了從點到區間再從區間到點的關系。詳細情況可以看一下另一位大佬博主的圖
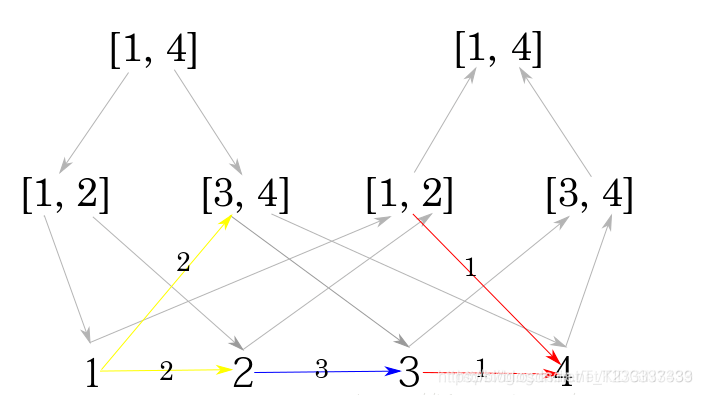
這個圖是進行了三個操作:
1 2 3 3 節點2到節點3有一條權值為3的邊(藍色)
2 1 2 4 2 節點1到區間[2,4]有權值為2的邊(黃色)
3 4 1 3 1 區間[1,3]到節點4有權值為1的邊(紅色)
再在這張圖上跑最短路(因為有0邊,最好還是用SPFA)
【AC代碼】
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<climits>
#include<cstdlib>
#include<cmath>using namespace std;typedef long long ll;const int MAXN=100005;
const ll INF=0x3f3f3f3f3f3f3f3f;
int head[MAXN<<2],ls[MAXN<<2],rs[MAXN<<2];
int root1,root2,tot,cnt;
struct edge
{int v,w,next;
}edge[MAXN*20];
ll dis[MAXN<<2];
queue<int> q;inline void AddEdge(int u,int v,int w)
{edge[++tot].v=v; edge[tot].w=w; edge[tot].next=head[u]; head[u]=tot;
}void build1(int &k,int l,int r)
{if(l==r){k=l; return;}k=++cnt;int mid=(l+r)>>1;build1(ls[k],l,mid); build1(rs[k],mid+1,r);AddEdge(k,ls[k],0); AddEdge(k,rs[k],0);
}void build2(int &k,int l,int r)
{if(l==r){k=l; return;}k=++cnt;int mid=(l+r)>>1;build2(ls[k],l,mid); build2(rs[k],mid+1,r);AddEdge(ls[k],k,0); AddEdge(rs[k],k,0);
}void update1(int k,int l,int r,int x,int L,int R,int w)
{if(l>=L && r<=R){AddEdge(x,k,w);return;}int mid=(l+r)>>1;if(L<=mid) update1(ls[k],l,mid,x,L,R,w);if(R>mid) update1(rs[k],mid+1,r,x,L,R,w);
}void update2(int k,int l,int r,int x,int L,int R,int w)
{if(l>=L && r<=R){AddEdge(k,x,w);return;}int mid=(l+r)>>1;if(L<=mid) update2(ls[k],l,mid,x,L,R,w);if(R>mid) update2(rs[k],mid+1,r,x,L,R,w);
}void SPFA(int s)
{memset(dis,0x3f,sizeof(dis));dis[s]=0; q.push(s);while(!q.empty()){int u=q.front(); q.pop();for(int i=head[u];i;i=edge[i].next){int v=edge[i].v,w=edge[i].w;if (dis[u]+w<dis[v]) dis[v]=dis[u]+w,q.push(v);}}
}int main()
{int n,m,s;int cmd,l,r,v,w,u;scanf("%d%d%d",&n,&m,&s);cnt=n; tot=0;build1(root1,1,n); build2(root2,1,n);for(int i=0;i<m;i++){scanf("%d",&cmd);if(cmd==1){scanf("%d%d%d",&u,&v,&w);AddEdge(u,v,w);}else{scanf("%d%d%d%d",&v,&l,&r,&w);if(cmd==2)update1(root1,1,n,v,l,r,w);elseupdate2(root2,1,n,v,l,r,w);}}SPFA(s);for(int i=1;i<=n;i++){cout<<(dis[i]<INF?dis[i]:-1)<<" ";}return 0;
}









)









