1. 紅黑樹的概念

紅黑樹是一種自平衡二叉查找樹，是在計算機科學中用到的一種數據結構，典型用途是實現關聯數組。它在1972年由魯道夫·貝爾發明，被稱為「對稱二叉B樹」，它現代的名字源于Leo J. Guibas和羅伯特·塞奇威克于1978年寫的一篇論文。紅黑樹的結構復雜，但它的操作有著良好的最壞情況運行時間，并且在實踐中高效：它可以在O(log n)時間內完成查找、插入和刪除，這里的n是樹中元素的數目。紅黑樹是每個節點都帶有顏色屬性的二叉查找樹，顏色為紅色或黑色。在二叉查找樹強制一般要求以外，對于任何有效的紅黑樹我們增加了如下的額外要求：節點是紅色或黑色。根是黑色。所有葉子都是黑色（葉子是NIL節點）。每個紅色節點必須有兩個黑色的子節點。從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點。
在紅黑樹中，所有的葉子結點都是黑色的空節點（NIL節點）。NIL節點是紅黑樹額外引入的結點，在計算紅黑數高度時NIL結點也會被計算在內。NIL結點指的是葉結點空的左右子結點延伸出來的的結點，也包括了葉子節點本身。
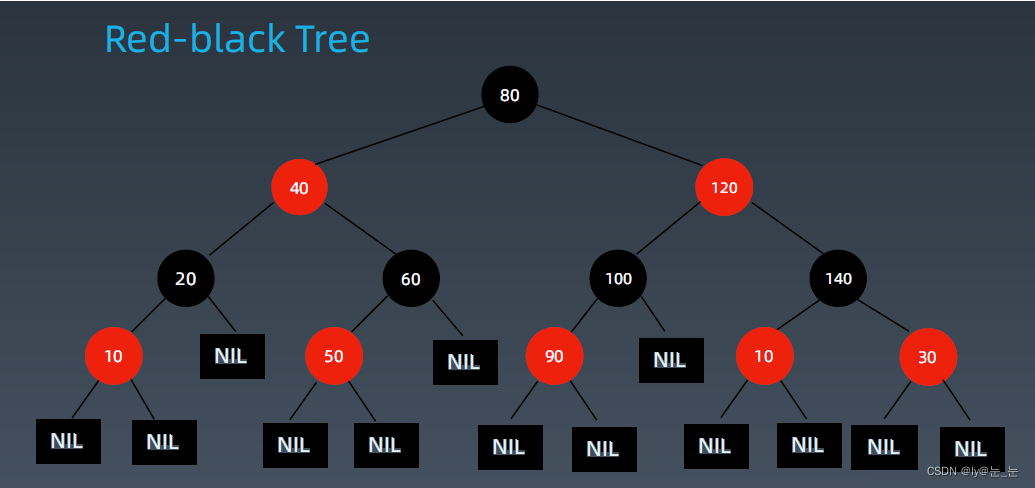
在這里插入圖片描述

2. 紅黑樹的性質

每個結點不是紅色就是黑色；
根節點是黑色的；
如果一個節點是紅色的，則它的兩個孩子結點是黑色的；
對于每個結點，從該結點到其所有后代葉結點的簡單路徑上，均包含相同數目的黑色結點；
每個葉子結點都是黑色的( 此處的葉子結點指的是空結點(NIL節點) )。

這些約束確保了紅黑樹的關鍵特性：從根到葉子的最長的可能路徑不多于最短的可能路徑的兩倍長。結果是這個樹大致上是平衡的。因為操作比如插入、刪除和查找某個值的最壞情況時間都要求與樹的高度成比例，這個在高度上的理論上限允許紅黑樹在最壞情況下都是高效的，而不同于普通的二叉查找樹。

3. 紅黑樹節點的定義

// 節點的顏色
enum Color{RED, BLACK};
// 紅黑樹節點的定義
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;   // 節點的左孩子RBTreeNode<K, V>* _right;  // 節點的右孩子RBTreeNode<K, V>* _parent; // 節點的雙親(紅黑樹需要旋轉，為了實現簡單給出該字段)pair<K, V> _kv;            // 節點的值Colour _col;               // 節點的顏色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)  //默認為紅節點{}
};

插入紅色節點樹的性質可能不會改變，而插入黑色節點每次都會違反性質4，所以將節點設置為紅色在插入時對紅黑樹造成的影響是小的，而黑色的影響是最大的

4. 紅黑樹的插入操作

紅黑樹是在二叉搜索樹的基礎上加上其平衡限制條件，因此紅黑樹的插入可分為兩步：

按照二叉搜索的樹規則插入新節點；
檢測新節點插入后，紅黑樹的性質是否造到破壞，如過性質被破壞，就要進行旋轉或變色的操作，此時需要對紅黑樹分情況來討論：
以下為父節點在祖父的左邊
對于紅黑樹的插入來說，如果插入的父節點為黑，并且插入的節點默認為紅節點，所以如果父節點為黑色時，插入是不需要進行調節的，如圖1->2：

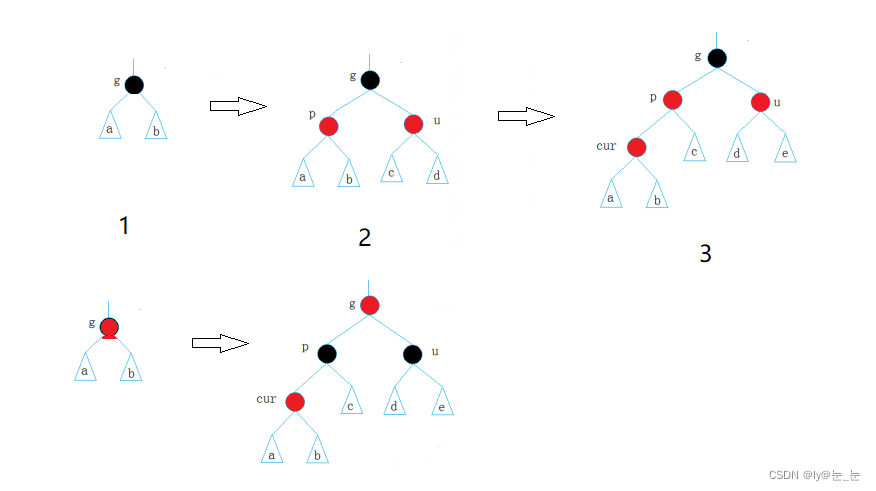
在這里插入圖片描述
有2->3圖可以看出cur、p兩個紅節點相連，所以需要調整，這種情況計為情況一：cur為紅，p為紅，g為黑，u存在且為紅。（約定:cur為當前節點，p為父節點，g為祖父節點，u為叔叔節點）
unlce節點的作用： 在紅黑樹中，uncle節點是指當前節點的父節點的兄弟節點。它的作用是在插入新節點時，如果當前節點的父節點和uncle節點都是紅色，那么需要將當前節點的父節點和uncle節點染成黑色，將當前節點的祖父節點染成紅色，然后以祖父節點為當前節點進行下一輪操作。這樣可以保證紅黑樹的性質4（每個紅色節點必須有兩個黑色的子節點）不被破壞。
對圖3進行調整，需要保證紅色節點不能相連，并且從該結點到其所有后代葉結點的簡單路徑上，均包含相同數目的黑色結點。如果只將cur改為黑色，那么違反規則4；將cur和uncle改為黑色，也會違反規則四，因為如果這棵樹是一個子樹，那么g結點的左右路徑是會多一個黑色結點。那么如何調整？
解決方式：將p,u改為黑，g改為紅，然后把g當成cur，繼續向上調整（因為g的父節點可能為紅色）。 這樣保證了每條路徑上的黑色結點的個數都相同。
對于變色來說，不論cur在parent的左邊還是右邊，變色后各個節點的位置都沒有改變，所以不需要分類討論。
代碼如下：

while (parent && parent->_col == RED)
{Node* grandfather = parent->_parent;if (grandfather->_left == parent){//情況1:uncle存在且為紅Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//繼續向上調整cur = grandfather;parent = cur->_parent;}}
}

cur為parent的左邊，如下圖又該怎樣調整？
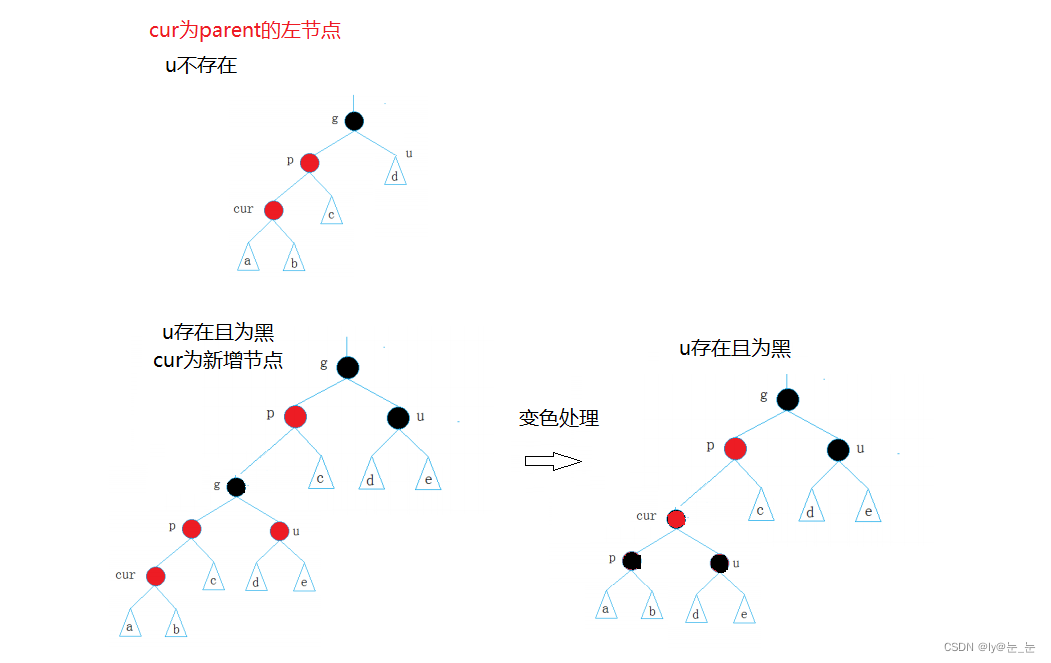
在這里插入圖片描述

說明: u的情況有兩種
1.如果u節點不存在，則cur一定是新插入節點，因為如果cur不是新插入節點,則cur和p一定有一個節點的顏色是黑色，就不滿足性質4:每條路徑黑色節點個數相同；這時就需要旋轉+變色處理。
2.如果u節點存在，則其一定是黑色的，那么cur節點原來的顏色一定是黑色的，現在看到其是紅色的原因是因為cur的子樹在調整的過程中將cur節點的顏色由黑色改成紅色。（如上圖下半部分所示）
計上述情況為情況二: cur為紅，p為紅，g為黑，u不存在/u存在且為黑
對于上述兩種情況我們發現怎么變色都是不行的，所以可以旋轉+變色處理。旋轉的詳解如本篇博客（AVL樹）
p為g的左孩子，cur為p的左孩子，則進行右單旋轉；相反，p為g的右孩子，cur為p的右孩子，則進行左單旋轉
p、g變色–p變黑，g變紅

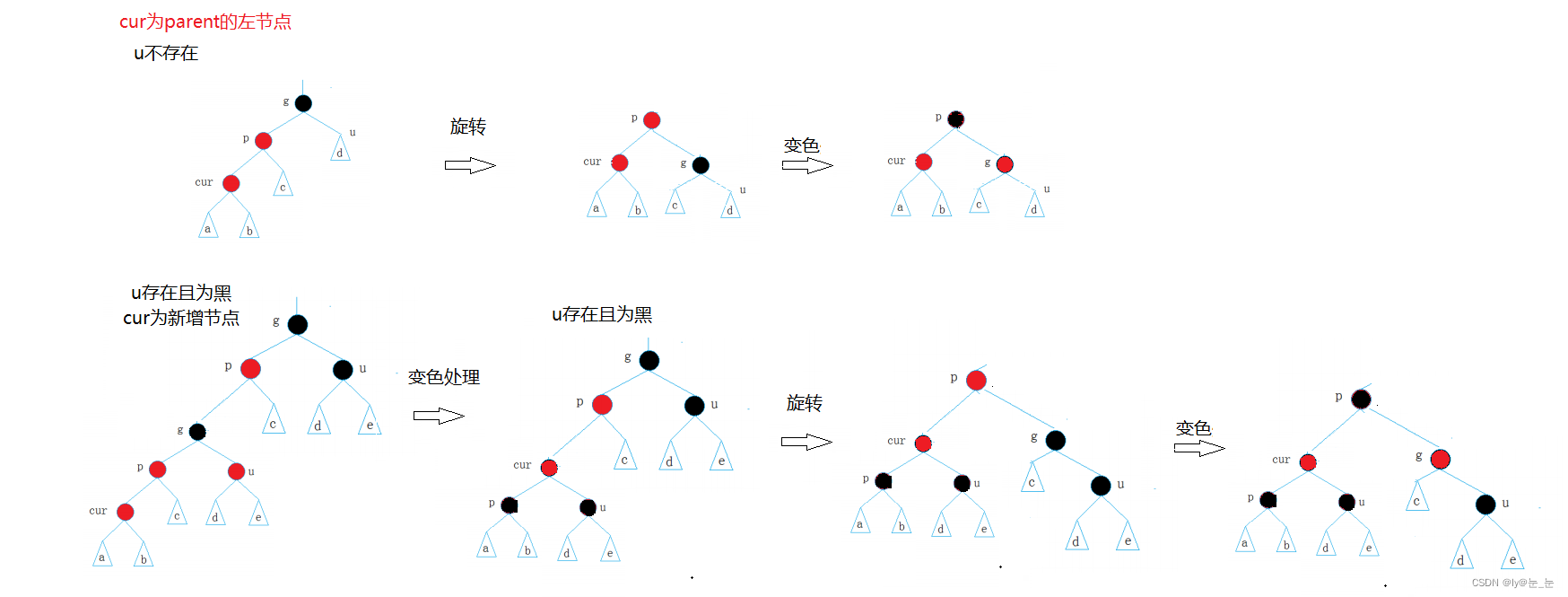
cur為parent的右邊，如下圖又該怎樣調整？
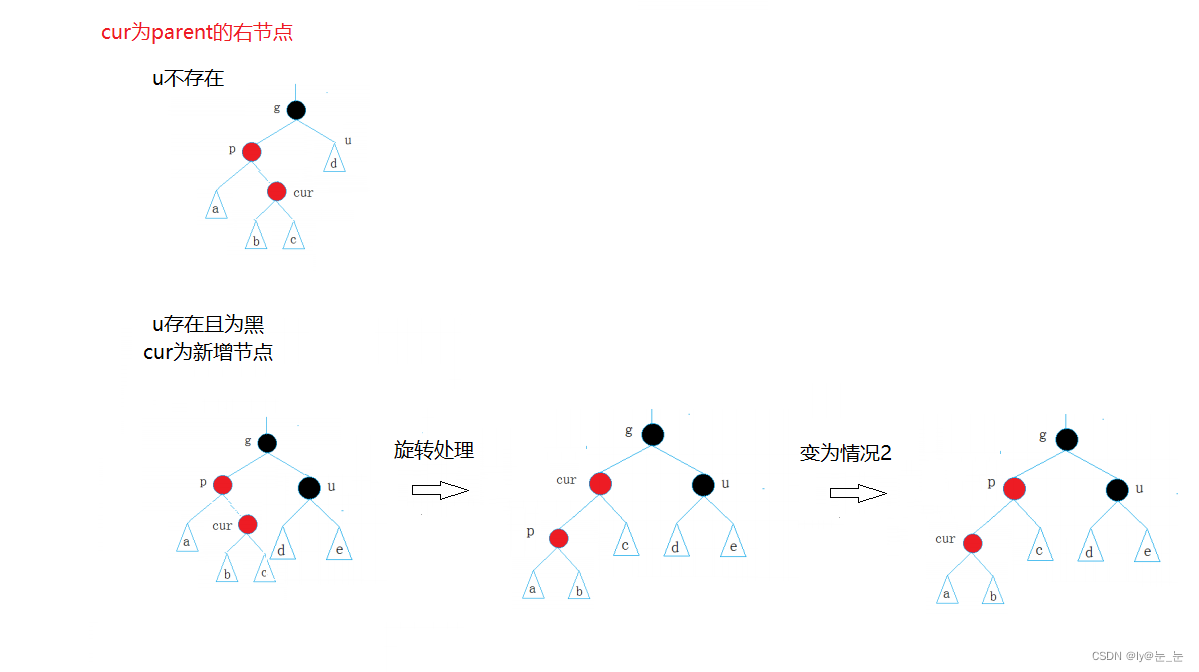
在這里插入圖片描述
上述情況記為情況三: cur為紅，p為紅，g為黑，u不存在/u存在且為黑
p為g的左孩子，cur為p的右孩子，則針對p做左單旋轉；相反，p為g的右孩子，cur為p的左孩子，則針對p做右單旋轉則轉換成了情況2。
如下圖進行旋轉+變色：
在這里插入圖片描述

代碼如下：

// 情況2和情況三3：u不存在/u存在且為黑，旋轉+變色//     g//   p   u// c 
//cur為父親節點的左邊
if (cur == parent->_left)
{RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;
}
//cur為父親節點的右邊，在右邊，需要雙旋（如AVL樹中的旋轉）
else
{//     g//   p   u//    cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;
}

對于父節點在祖父節點的右邊，這種情況和上述大致相同，就不在多畫了，完整代碼如下。
RBTree.h文件中的代碼：

#pragma onceenum Colour
{RED,BLACK,
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;   // 節點的左孩子RBTreeNode<K, V>* _right;  // 節點的右孩子RBTreeNode<K, V>* _parent; // 節點的雙親(紅黑樹需要旋轉，為了實現簡單給出該字段)pair<K, V> _kv;            // 節點的值Colour _col;               // 節點的顏色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first > key){cur = cur->_left;}else if (cur->_kv.first < key){cur = cur->_right;}else{return cur;}}return nullptr;}bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//尋找插入的位置Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_kv > kv){cur = cur->_left;}else if (cur->_kv < kv){cur = cur->_right;}else{return false;}}//插入新節點cur = new Node(kv);if (parent->_kv > kv){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//進行調整這棵紅黑樹while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//父節點在祖父的左邊if (grandfather->_left == parent){//情況1:uncle存在且為紅Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//繼續向上調整cur = grandfather;parent = cur->_parent;}else  //叔叔不存在或叔叔存在且為黑,旋轉+變黑{//cur為父親節點的左邊if (cur == parent->_left){//     g//   p   u// c RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else  //cur為父親節點的右邊{//     g//   p   u//    c RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}//父節點在祖父的右邊else // (grandfather->_right == parent){//    g//  u   p//        cNode* uncle = grandfather->_left;// 情況1：u存在且為紅，變色處理，并繼續往上處理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 繼續往上調整cur = grandfather;parent = cur->_parent;}else // 情況2+3：u不存在/u存在且為黑，旋轉+變色{//    g//  u   p//        cif (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{//    g//  u   p//     cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//確保每次調整完后根節點為黑色_root->_col = BLACK;return true;}//因為紅黑樹的結點是new出來的，所以需要釋放，也就是需要寫析構函數~RBTree(){_Destroy(_root);_root = nullptr;}int Height(){return _Height(_root);}void InOrder(){_InOrder(_root);}
private:int _Height(Node* root){if (root == NULL)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}void _Destroy(Node* root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete(root);}
private:Node* _root = nullptr;
};

測試代碼：

#include <iostream>
using namespace std;#include "RBTree.h"void Test_RBTree1()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14, 16, 3, 7, 11, 9, 26, 18, 14, 15 };RBTree<int, int> t1;for (auto e : a){t1.Insert(make_pair(e, e));}t1.InOrder();
}
int main()
{Test_RBTree1();return 0;
}

運行結果如下：
在這里插入圖片描述

5. 紅黑樹與AVL樹的比較

1.紅黑樹和AVL樹都是高效的平衡二叉樹，增刪改查的時間復雜度都是O(log N)，但它們的實現方式不同。
2.紅黑樹的查詢性能略微遜色于AVL樹，因為其比AVL樹會稍微不平衡最多一層，也就是說紅黑樹的查詢性能只比相同內容的AVL樹最多多一次比較。
3.紅黑樹不追求絕對平衡，其只需保證最長路徑不超過最短路徑的2倍，紅黑樹在插入和刪除上優于AVL樹，AVL樹每次插入刪除會進行大量的平衡度計算，而紅黑樹為了維持紅黑性質所做的紅黑變換和旋轉的開銷，相較于AVL樹為了維持平衡的開銷要小得多。所以在經常進行增刪的結構中性能比AVL樹更優，而且紅黑樹實現比較簡單，所以實際運用中紅黑樹更多。