計算機圖形學畫線

計算機圖形學| 直接使用線方程 (Computer Graphics | Direct Use of Line Equation)

The standard line equation, as we all know is used for drawing a line. It is given by: y = mx + c.

眾所周知，標準線方程式用于繪制線。 由下式給出： y = mx + c 。

We are discussing here in 2D so we all know that there are 2 axes: x and y. Both of the axes are required to give the equation of any 2D shape. The line is a straight path joining 2 points in the x-y plane. If both the points are given then we can find the equation of a line.

我們在這里以2D進行討論，所以我們都知道有2個軸： x和y 。 需要兩個軸都可以給出任何2D形狀的方程。 該線是連接xy平面中2個點的直線路徑。 如果兩個點都給出，那么我們可以找到一條線的方程。

直線的斜率 (The slope of a line)

The slope of a line defines the direction of a line. Its value is equal to the ratio of the difference of y coordinates and the difference. Assume that the two points are X( x1,y1 ) and Y( x2,y2 ). Its slope, 'm' will be: m = (y2 - y1) / (x2 - x1).

線的斜率定義了線的方向。 它的值等于y坐標差與差之比。 假設這兩個點是X(x1，y1)和Y(x2，y2) 。 它的斜率'm'將是： m =(y2-y1)/(x2-x1) 。

線描算法的性質 (Properties of Line Drawing Algorithm)

The following are the properties that a line must hold in any line drawing algorithm,

以下是任何線圖繪制算法中線必須具有的屬性，

1. Line must be straight

   線必須是直的

2. Line must terminate accurately

   線路必須準確終止

3. Line must have constant density

   線必須具有恒定的密度

4. Density must be independent of its length

   密度必須與長度無關

5. Line must be drawn very fast

   線必須畫得很快

線描算法 (Line Drawing Algorithms)

There are some set of rules and steps which help draw a line. These algorithms are given below,

有一些規則和步驟可以幫助您劃清界限。 這些算法如下：

1. Direct Use of line equation

   直接使用線方程

2. DDA (Digital Differential Analyzer)

   DDA(數字差分分析儀)

3. Bresenham's Algorithm

   布雷森納姆算法

直接使用線方程 (Direct use of Line Equation)

This is the simplest form of drawing a line. We all know that the equation of the line is y = mx + c. Here m is slope and c is the length from origin to the point where the line cuts y-axis. In this method, we will be having the start and endpoint of the line and by the help of that points, we'll calculate the other points which lie on the line. We have to find the slope of the line by using the given points.

這是畫線的最簡單形式。 我們都知道直線的方程是y = mx + c 。 這里的m是斜率， c是從原點到直線切割y軸的點的長度。 在這種方法中，我們將獲得直線的起點和終點，并借助這些點，計算出直線上的其他點。 我們必須使用給定的點找到線的斜率。

We'll understand this better with the help of an example,

我們將通過一個示例來更好地理解這一點，

Example:

例：

We have given two points X and Y. The coordinates of X are (0, 0) and the coordinates of Y are (5, 15). The slope of the line will be,

我們給出了X和Y兩點。 X的坐標為(0，0) ， Y的坐標為(5，15) 。 線的斜率是

    m = (15 - 0) / (5-0)
m = 3

We have the slope of the line. Now let us put the slope in the line equation.

我們有直線的斜率。 現在讓我們將斜率放在線方程中。

    y = 3x + c

Origin point is (0,0). So,

原點是(0,0)。 所以，

    c = 0

Putting c=0 in the above equation.

將c = 0放在上式中。

    y = 3x

Now we will calculate the intermediate points.

現在我們將計算中間點。

    Let x = 1 ? y = 3 x 1 ? y = 3
Let x = 2 ? y = 3 x 2 ? y = 6
Let x = 3 ? y = 3 x 3 ? y = 9
Let x = 4 ? y = 3 x 4 ? y = 12
Let x = 5 ? y = 3 x 5 ? y = 15

We got the intermediate points which are, (1, 3), (2, 6), (3, 9), (4, 12) and finally (5, 15)

我們得到的中間點是(1、3)，(2、6)，(3、9)，(4、12)，最后是(5、15)

Now we'll plot these points on the graph.

現在，我們將這些點繪制在圖形上。

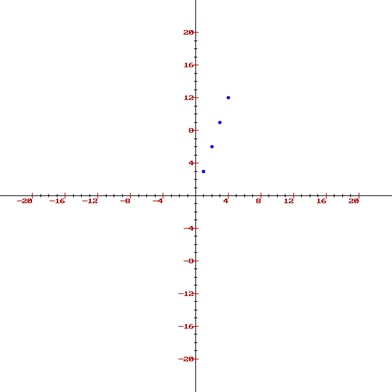
Hence, we have plotted the points that lie between the given points through the standard line equation. By doing so with a very small gap between these pints will give us the entire line.

因此，我們通過標準線方程式繪制了位于給定點之間的點。 這樣，這些品脫之間的間隙很小，就可以給我們整條生產線。

翻譯自: https://www.includehelp.com/computer-graphics/direct-use-of-line-equation.aspx

計算機圖形學畫線