---

一些概念、函數、用法

對象Variable

創建對象Variable：

tf.Variable(initial_value,dtype)

利用這個方法，默認整數為int32，浮點數為float32，注意Numpy默認的浮點數類型是float64，如果想和Numpy數據進行對比，則需要修改與numpy一致，否則在機器學習中float32位夠用了。
將張量封裝為可訓練變量

print(tf.Variable(tf.random. normal([2,2])))

<tf.Variable ‘Variable:0’ shape=(2, 2) dtype=float32, numpy=array([[-1.2848959 , -0.22805293],[-0.79079854, 0.7035335 ]], dtype=float32)>

trainalbe屬性
用來檢查Variable變量是否可訓練

x.trainalbe

可訓練變量賦值，注意x是Variable對象類型，不是tensor類型

x.assign()
x.assign_add()
x.assign_sub()

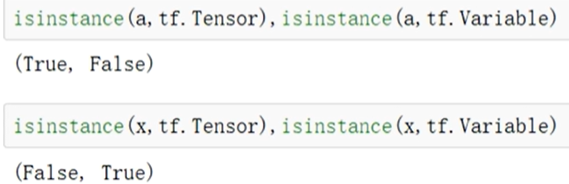
用isinstance()方法來判斷是tensor還是Variable

自動求導

with GradientTape() as tape:
函數表達式
grad=tape.gradient(函數，自變量)

x=tf.Variable(3.)
with tf.GradientTape() as tape:y=tf.square(x)
dy_dx = tape.gradient(y,x)
print(y)
print(dy_dx)

tf.Tensor(9.0, shape=(), dtype=float32)
tf.Tensor(6.0, shape=(), dtype=float32)

GradientTape函數

GradientTape(persistent，watch_accessed_variables)
第一個參數默認為false，表示梯度帶只使用一次，使用完就銷毀了，若為true則表明梯度帶可以多次使用，但在循環最后要記得把它銷毀
第二個參數默認為true，表示自動添加監視

tape.watch()函數
用來添加監視非可訓練變量
多元函數求一階偏導數

x=tf.Variable(3.)
y=tf.Variable(4.)
with tf.GradientTape(persistent=True) as tape:f=tf.square(x)+2*tf.square(y)+1
df_dx,df_dy = tape.gradient(f,[x,y])
first_grade = tape.gradient(f,[x,y])
print(f)
print(df_dx)
print(df_dy)
print(first_grade)
del tape

tf.Tensor(42.0, shape=(), dtype=float32)
tf.Tensor(6.0, shape=(), dtype=float32)
tf.Tensor(16.0, shape=(), dtype=float32)
[<tf.Tensor: id=36, shape=(), dtype=float32, numpy=6.0>, <tf.Tensor: id=41, shape=(), dtype=float32, numpy=16.0>]

多元函數求二階偏導數

x=tf.Variable(3.)
y=tf.Variable(4.)
with tf.GradientTape(persistent=True) as tape2:with tf.GradientTape(persistent=True) as tape1:f=tf.square(x)+2*tf.square(y)+1first_grade = tape1.gradient(f,[x,y])
second_grade = [tape2.gradient(first_grade,[x,y])]
print(f)
print(first_grade)
print(second_grade)
del tape1
del tape2

tf.Tensor(42.0, shape=(), dtype=float32)
[<tf.Tensor: id=27, shape=(), dtype=float32, numpy=6.0>, <tf.Tensor: id=32, shape=(), dtype=float32, numpy=16.0>]
[[<tf.Tensor: id=39, shape=(), dtype=float32, numpy=2.0>, <tf.Tensor: id=41, shape=(), dtype=float32, numpy=4.0>]]

TensorFlow實現一元線性回歸

import numpy as np
import tensorflow as tf 
import matplotlib.pyplot as plt 
#設置字體
plt.rcParams['font.sans-serif'] =['SimHei']
#加載樣本數據
x=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
#設置超參數,學習率
learn_rate=0.0001
#迭代次數
iter=100
#每10次迭代顯示一下效果
display_step=10
#設置模型參數初值
np.random.seed(612)
w=tf.Variable(np.random.randn())
b=tf.Variable(np.random.randn())
#訓練模型
#存放每次迭代的損失值
mse=[]
for i in range(0,iter+1):with tf.GradientTape() as tape:pred=w*x+bLoss=0.5*tf.reduce_mean(tf.square(y-pred))mse.append(Loss)#更新參數dL_dw,dL_db = tape.gradient(Loss,[w,b])w.assign_sub(learn_rate*dL_dw)b.assign_sub(learn_rate*dL_db)#plt.plot(x,pred)if i%display_step==0:print("i:%i,Loss:%f,w:%f,b:%f"%(i,mse[i],w.numpy(),b.numpy()))

TensorFlow實現多元線性回歸

import numpy as np
import tensorflow as tf #=======================【1】加載樣本數據===============================================
area=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
room=np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])
price=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
num=len(area) #樣本數量
#=======================【2】數據處理===============================================
x0=np.ones(num)
#歸一化處理，這里使用線性歸一化
x1=(area-area.min())/(area.max()-area.min())
x2=(room-room.min())/(room.max()-room.min())
#堆疊屬性數組，構造屬性矩陣
#從(16,)到(16,3),因為新出現的軸是第二個軸所以axis為1
X=np.stack((x0,x1,x2),axis=1)
print(X)
#得到形狀為一列的數組
Y=price.reshape(-1,1)
print(Y)
#=======================【3】設置超參數===============================================
learn_rate=0.001
#迭代次數
iter=500
#每10次迭代顯示一下效果
display_step=50
#=======================【4】設置模型參數初始值===============================================
np.random.seed(612)
W=tf.Variable(np.random.randn(3,1))
#=======================【4】訓練模型=============================================
mse=[]
for i in range(0,iter+1):with tf.GradientTape() as tape:PRED=tf.matmul(X,W)Loss=0.5*tf.reduce_mean(tf.square(Y-PRED))mse.append(Loss)#更新參數dL_dw = tape.gradient(Loss,W)W.assign_sub(learn_rate*dL_dw)#plt.plot(x,pred)if i % display_step==0:print("i:%i,Loss:%f"%(i,mse[i]))

---

喜歡的話點個贊和關注唄！