給你一個二叉樹的根節點?root?，判斷其是否是一個有效的二叉搜索樹。

有效?二叉搜索樹定義如下：

• 節點的左子樹只包含?小于?當前節點的數。
• 節點的右子樹只包含?大于?當前節點的數。
• 所有左子樹和右子樹自身必須也是二叉樹

? ? ? ?二叉樹滿足以上3個條件，有些同學就會說，BST不就是左大右小么？我直接判斷root.val>root.left.val 和root.val<root.right.val不就可以了么？

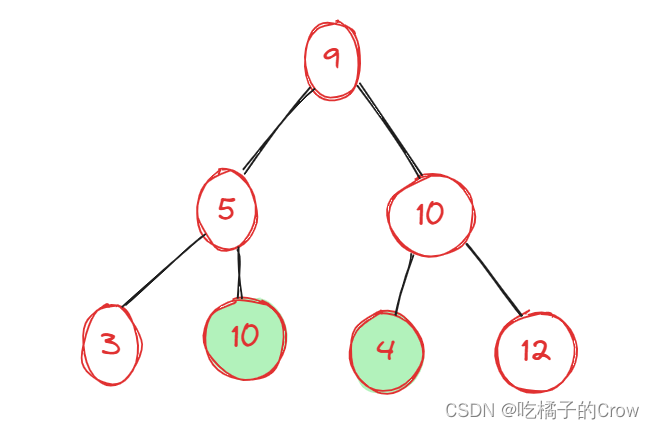
? ? ? ? ?這樣肯定是不對的，因為BST左小右大的特性是指root.val要比左子樹的所有節點要大，要比右子樹上的所有節點要小，所以只是檢查兩個節點當前是不夠的，我們可以通過輔助函數，增加函數參數列表，在參數中攜帶額外信息，將下一個節點的合理取值范圍傳遞下去，進行判斷

因為root節點開始沒有范圍的限制，所以我們對其的邊界可以最小的無窮，最大也是無窮

isValidBST(root,Integer.MIN_VALUE,Integer.MAX_VALUE);

如果當前節點不符合合法邊界，直接返回false

 if(node.val<=lower||node.val>=upper){return false;}

去遍歷當前節點的左子樹和右子數，并更新取值范圍

isValidBST(node.left,lower,node.val)&&isValidBST(node.right,node.val,upper);

結果：

? ? ? ?看到測試案例頓時豁然開朗，一看這種比較大的數，一看就是數值類型的問題，超出范圍了，然后我們將Integer改為更大的Long,然后：

?