糾錯碼和壓縮算法是同一枚硬幣的兩面。
兩者都來自于對冗余的想法。 糾錯碼被視為向消息或文件中添加冗余的原則性方法。而壓縮算法正好相反,他們會從消息或文件中移除冗余。
壓縮和糾錯并不是彼此抵消的,相反,好的壓縮算法會移除抵消冗余,而糾錯編碼會增加另一種更高效的冗余。
因此首先壓縮一條信息,再往里面添加一些糾錯碼的做法十分常見。 下面分別介紹兩者的具體內容:
糾錯碼trick
如果使用正確的技巧,即使是極端不可靠的通信頻道也可以以極低的錯誤率傳輸數據。
1、重復技巧
要確保一些信息被正確傳輸,你只需要重復幾次該信息。
如果你的賬戶余額是5213.75美元,但不幸的是,網絡不穩定,每個數字都有20%的概率變成其他數字
通過運用重復技巧,可以推測真正的余額:假設你請求傳輸余額5次,并收到如下反饋:
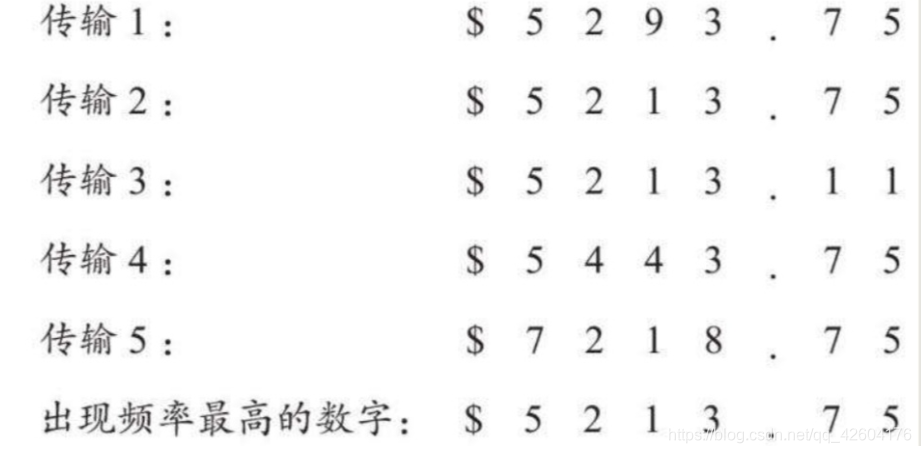
只要我們增加重新傳輸的次數,直到可靠性高到我們滿意為止。
相反,如果一個惡意實體故意干擾傳輸,并選擇制造某些錯誤,重復技巧將變得不可靠。
并且在下載一個大型軟件,顯然傳輸多次以確保正確性是不成熟的。
2、冗余技巧
基本原則:不能只發送原始消息,要發送一些多余的東西以增加可靠性,這里我們討論的是把原始消息轉換成一條更加長的冗余消息,原始消息會被刪除。
還是以銀行余額為例:
如果你的賬戶余額是5213.75美元
我們用英語單詞簡單地拼出余額:
five two one three point seven five
由于信道糟糕,這條消息中約20%的字符會變成隨機字符,這條消息可能會變成:
fiqe kwo one thrxp point sivpn fivq
如果我們告訴你對消息中的任何單個變化進行可靠偵測以及糾正變得顆星,我們絕對可以猜出原始消息中的單詞。
但是如果我告訴你"367"代表了一個數,但其中一個數字被替換了,你就沒辦法直道原始數字是多少了,因為這條消息中沒有冗余。
冗余和讓消息變長有關,消息的每一部分都應該符合某種已知模式。通過這種方法,任何變化都能首先被識別,然后被糾正。
冗余的工作機理:消息由符號組成
要傳輸一條消息:
1、首先要找出每個符號,并將符號轉譯成對應的代碼字。
2、然后,將轉換的消息通過不可靠信道發送。
3、當消息被接收時,查看消息的每個部分,檢查其是否為有效的代碼字。如果是有效的,只需將其轉換為相應的符號,如果不是有效的代碼字,你就要找出它和哪個代碼字最匹配

由理查德漢明于貝爾實驗室發明的代碼和我們相比最明顯的區別就是將所有事情都通過0和1完成:
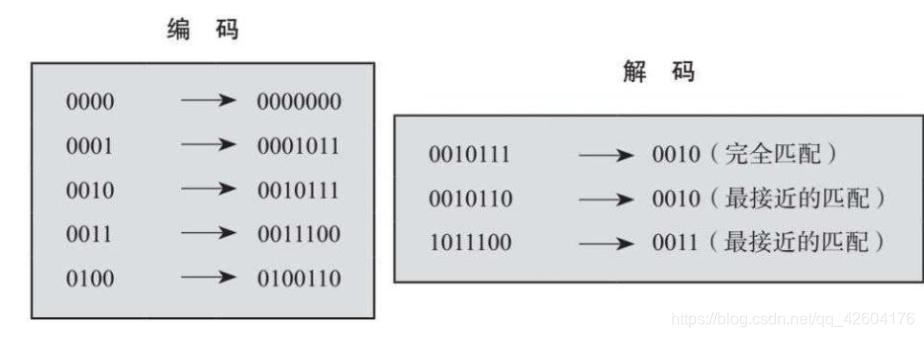
在編碼時,每一組4位數字都加入了冗余,由此產生了一個7位數的代碼字。
解碼時,首先尋找完全匹配,否則選擇最接近匹配。這里我們不深究7位數代碼字中的設計。
3、冗余和重復比較
通常用雜項(overhead)衡量糾錯系統的成本。雜項就是為確保消息被正確接收而發送的多余信息。
重復技巧的雜項數量巨大,因為你必須發送數份完整消息。
冗余技巧的雜項取決于使用的代碼字的具體類型。
4、校驗和技巧
上面的兩個技巧都屬于同時偵測和糾正數據中錯誤的方法。
還有一種思路:可以先不管糾錯,而是將精力集中在偵測錯誤上。對于許多應用場景,只偵測到一個錯誤就足夠了,然后請求再發送一份數據即可,可以一直請求拷貝,直到得到完全無誤的拷貝,我們稱之為校驗和技巧。
簡單校驗和:將消息中的所有數字相加,只保留結果的最后一位數作為簡單校驗和
例:假設消息為 4 6 7 5 6,所有數字之和:4+6+7+5+6=28,保留最后一位數,因此這條消息的簡單校驗和是8.
在發送原始消息前,將原始消息的校驗和附加到消息末尾即可。別人在接收消息后,就能再次計算校驗和,并和你發送的校驗和比較,看收到的消息是否正確。
缺點:簡單校驗和最多只能在消息中偵測出一處錯誤,如果有兩個或者更多錯誤,簡單校驗和可能就偵測不到了。

我們定義一種新的校驗和,階梯校驗和:每個數都和該數字所在的位階相乘,每個數都比前一個數大一個位階,最后只保留最后一位數。
假如消息為4 6 7 5 6,階梯校驗和計算:
(1x4) +(2x6)+(3x7)+(4x5)+(5x6)=87,保留最后一位數,為7,所以階梯校驗和為7;

只要錯誤不超過兩處,你就能用這兩種方法,偵測到錯誤。
上面描述的校驗和技巧只生成了兩個校驗和數字,但真正的校驗和通常會生成很長的數字。
重點是,校驗和的長度是固定的。對非常長的消息來說,即使一個較大的校驗和,最終和消息本身相比也極小。(校驗和長度越長,偵測錯誤失敗概率越小,在現實中幾乎不可能失敗)
當存在惡意攻擊而非糟糕信道時,采用加密哈希函數的特定校驗和效果較好。
5、定位技巧
此處介紹一種特殊的冗余技巧,它能讓你迅速定位一處錯誤,我們稱之為定位技巧。
假設消息有16個數字(如果有一條長消息,將其打碎成16位數據的“塊”,并單獨處理每塊數據;如果消息比16個數字短,就用0把它補成16位數)
第一步:重新排列消息中的16個數,將其排列成一個從左往右、自上向下讀的方框:
4 8 3 7 5 4 3 6 2 2 5 6 3 9 9 7
重新排列為:

計算每一行的簡單校驗和,并添加在每行的右側:

計算每一列的簡單校驗和,并添加在每列的底側:

重新排列所有數,讓其能以一次一個數的方式被存儲或傳輸,然后通過從左往右、自上而下的方式讀數,最后會得到如下24位數的消息:
4 8 3 7 2 5 4 3 6 8 2 2 5 6 5 3 9 9 7 8 4 3 0 6
把數字放入一個5x5的方框中,最后一行和最后一列都對應隨原始消息一起被發送的校驗和數字:

接下來,計算每一行每一列4個數的簡單校驗和,在接收的校驗和值旁邊新建一行和一列:

這里會出現兩組校驗和:1個是你發送的,1個是你接收的
如果它們都一樣,那么可以確定收到的消息很可能是正確的。那么出一個錯誤呢?

我們可以很快定位出出錯位置,那么我們該如何糾正呢?
我們只要用一個能讓兩個校驗和都正確的數字替代出錯的那個數字就可:第二列校驗和本應該是3,但結果是8,也就是說校驗和要減去5,7-5=2。

將糾正后的原始16位數消息從5x5的框中取出,忽略最后一行和最后一列,從左往右從上往下取出:
4 8 3 7 5 4 3 6 2 2 5 6 3 9 9 7
這種定位技巧我們稱之為二維奇偶校驗碼,奇偶校驗碼和簡單校驗和的意思一樣。二維奇偶校驗碼在一些真正的計算機系統中也有運用,但是并不如其他一些冗余技巧高效。
不過它很容易地具化并展現出不要求復雜數學的情況下,在計算機系統中的流行代碼背后發現并糾正錯誤。
數據壓縮trick
數據壓縮分為無損壓縮和有損壓縮
無損壓縮
無損壓縮需要了解的技巧:
1、行程長度編碼:將重復的“行程”和行程的“長度”編碼在一起;
例如:AAAAABCBCBCBCAAAADEFDEF可以被編碼為:5A、4BC、4A、2DEF
將23個字母壓縮為只有11個字母的字符串。
主要問題:數據中心重復的片段必須是相鄰的,不能有其他數據。
例如:ABABAB編碼很容易(3AB),但是ABXABYAB就行不通了。
2、同前技巧:
基于行程長度編碼的改進:
例如下面這個數據:
VJGDNQMYLH-KW-VJGDNQMYLH-ADXSGF-OVJG
DNQMYLH-ADXSGF-VJGDNQMYLH-EW-ADXSGF
忽略連字符,首先識別數據中重復的數據塊。
已知最開始12個字母沒有重復部分,但是接下來的10個字母VJGDNQMYLH與之前的有部分重合,可以說back12,copy10(數回12個字母,直至抄到第10個字母),接下來7個字母新出現,不能壓縮。后面的字母又是大的重復,可以縮寫。
我們縮寫b代替back,c代替copy,指令可以被總結如下:
VJGDNQMYLH-KW-b12c10-ADXSGF-O-b17c16-b16c10-EW-b18c6
下面一個例子:
使用相同的技巧壓縮FG-FG-FG-FG-FG-FG-FG-FG,消息中有8次重復。可以使用FG-FG-FG-FGb8c8,
更簡略的寫法:FG-b2c14,在口述最開始的兩個字母之后,我們有了FG,然后收到b2c14指令,抄完兩個之后結果為FG-FG,持續抄寫,直到抄寫到14個為止。
3、更短符號技巧:
使用頻率越高,編碼越短。
具體步驟:
1、計算機使用同前技巧傳輸未經壓縮的源文件,讓文件中絕大多數重讀的數據由短得多的指令取代,這些指令會返回并拷貝其他地方的數據
2、計算機檢查傳輸后的文件,選出經常出現的符號。隨后計算機會創建出一張表格,用短數字碼代表經常用到的符號,用更長的數字碼代表極少用到的符號。
3、計算機會通過直接將文件翻譯為2中的數字碼再次傳輸文件。2中計算出的數字碼表也會存儲到文件中,否則在后面不可能解碼。
有損壓縮:
有損壓縮需要了解的技巧:
1、拋棄技巧:以圖像為例,原圖像為320 x 240,每兩行或每兩列像素就拋棄一行或一列,結果得到解析度為160 x 120的新圖像。

可以發現,壓縮后的圖片重構之后的有較嚴重的壓縮缺陷。
接下來講解一下jpeg技術的基本原理:
jpeg首先將整張圖片劃分為8 x 8 的小方塊,每個方塊都被單獨壓縮,在沒有被壓縮的情況下,每個方塊代表64個數字(假設為灰度圖),如果這個方塊符合某些已知模式,如常數色(Constant Color)或漸變色(Smoothly Varying Color)的組合,那么其大部分信息都可以被拋棄,只需要存儲每個模式的級別或量即可
參考:【改變未來的九大算法】



)


函數以及C ++ STL中的示例)












