一、規則組織數學模型的建立
規則組織滿足兩個不變:1,組織點運動規律不變、2,飛數不變的單系統組織
即:若知道組織點運動規律和飛數即可確定唯一一個組織。

3上2下,組織循環數為3+2=5,經紗循環數=緯紗循環數=5,故意匠格的大小為5×5。
其對應的組織圖為: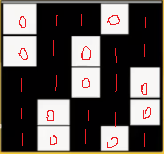
很容易理解:從下向上、從左向右
第一列:三個黑兩個白,(例如:黑為經組織點,白為緯組織點)
第二列:由于飛數是2,這里需要將每個位置都向上移動兩個單位
第三列:以此類推,超出的組織圖大小的組織點,從最底下向上依次補齊即可
為了讓計算機能夠識別,這時候需要引入二維數組進行標識,規定:在二維數組中,值為1時表示經組織點,值為0時表示緯組織點。
矩陣中的列數=經紗循環數,行數=緯紗循環數
這里使用N1代表行數即緯紗循環數,N2表示列數即經紗循環數。
通過二維數組:a[N1][N2]即可唯一表示一個單系統組織;即矩陣和組織圖之間時一一對應的關系。
經紗循環數即在一個組織中包含經紗的根數;同理,緯紗循環數即在一個組織中包含緯紗的根數。
對于組織而言,只有兩種形式:1,經紗在緯紗上,稱之為經組織點、1,緯紗在經紗上,稱之為緯組織點
二、矩陣的第一列賦值
組織的運動規律使用一個分式進行表示。
組織的一般形式:
c1上d1下,c2上d2下,c3上d3下…以此類推
ci表示連續的經組織點,di表示連續的緯組織點
分析:當得到組織圖時,如何定義出對應的二維矩陣
1,首先,組織圖都是從下往上,從左往右定義的,即左下角為起始位置,然后向上。對于一個規則組織來說,行數和列數是相同的,經紗循環數=緯紗循環數。
2,當拿到組織的一般形式時,需要先確定二維矩陣的大小,即行數和列數;只需要將所有的分子和分母都加到一塊即可得到二維矩陣的大小。
例如:3上2下2上1下,飛數為1的組織一般形式

之所以是8×8的二維矩陣,是因為3+2+2+1=8
故可以求出其經緯紗循環數N2和N1,即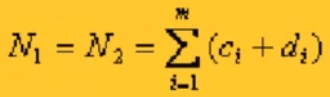
3,確定二維矩陣的大小后,開始求其中的每一個元素的值
想要畫出組織圖所對應的二維矩陣,需要先將第一列的值確定出來。
若取組織圖一般表達式,該分式的分子賦值為1,分母賦值為0
由于組織圖是由下向上進行表示的,組織中的組織點與二維數組中點的坐標剛好相反。
第一列的元素所對應的組織圖的位置為:N1-i+1
例如:N1=5
組織的一般表達式為: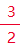
即,3上2下,上賦值為1,下賦值為0

3上,3個1 是先賦值給a5、a4、a3;2下,2個0再賦值給a2、a1
即對應的次序為N1-i+1
| 組織一般表達式(i代表緯紗,次序從下往上) | 運算 | 二維矩陣具體點 |
|---|---|---|
| i=1(第一根緯紗,最下面) | 5-1+1=5 | a5 |
| i=2 | 5-2+1=4 | a4 |
| i=3 | 5-3+1=3 | a3 |
| i=4 | 5-4+1=2 | a2 |
| i=5 | 5-5+1=1 | a1 |
4,確定表達式通式從而確定第一列所對應的矩陣值
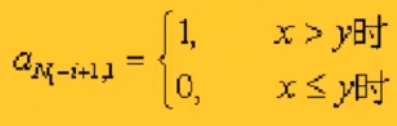 其中,x和y僅為兩個做判斷的任意變量,初始值均為0。
其中,x和y僅為兩個做判斷的任意變量,初始值均為0。當取分子時,x+1,y不變;取分母時,y+1,x不變。
例如:
| (經組織循環數=緯組織循環數)N1=N2=3+2+2+1=8 | c1=3 | d1=2 | c2=2 | d2=1 | 初始值:x=y=0 | 運算 | 二維數組對應值 |
|---|---|---|---|---|---|---|---|
| i=1(第一根緯紗) | c1=3(分子c1=3取下來,需要依次賦3個1) | 因為c1是分子,x=x+1=1,y=y=0 | N1-i+1=8 | 因為c1是分子,故a8=1 | |||
| i=2 | c1=c1-1=2 | 因為沒有取新的c和新的d,故x和y均保持不變,x=x=1,y=y=0 | N1-i+1=8-2+1 | 因為c1是分子,故a7=1 | |||
| i=3 | c1=c1-1=1 | 因為沒有取新的c和新的d,故x和y均保持不變,x=x=1,y=y=0 | N1-i+1=8-2+1 | 因為c1是分子,故a6=1 | |||
| i=4 | c1=c1-1=1-1=0,因為c1=0,故需要取下一個值,即d1=2 | d1=2 | 因為d1是分母,x=x=1,y=y+1=0+1=1 | N1-i+1=8-4+1 | 因為d1是分母,故a5=0 | ||
| i=5 | d1=d1-1=2-1=1 | 因為沒有取新的c和新的d,故x和y均保持不變,x=x=1,y=y=1 | N1-i+1=8-5+1 | 因為d1是分母,故a4=0 | |||
| i=6 | d1=d1-1=1-1=0,因為d1=0,故需要取下一個值,即c2=2 | c2=2 | 因為c2是分子,x=x+1=1+1=2,y=y=1 | N1-i+1=8-6+1 | 因為c2是分子,故a3=1 | ||
| i=7 | c2=c2-1=2-1=1 | 因為沒有取新的c和新的d,故x和y均保持不變,x=x=2,y=y=1 | N1-i+1=8-7+1 | 因為c2是分子,故a2=1 | |||
| i=8 | c2=c2-1=1-1=0,因為c2=0,故需要取下一個值,即d2=1 | d2=1 | 因為d2是分母,x=x=2,y=y+1=1+1=2 | N1-i+1=8-8+1 | 因為d2是分母,故a1=0 |
5,確定第二列矩陣值
第一列矩陣值確定之后,第二列的矩陣值主要取決于飛數,飛數為1,上移1格、飛數為-1,下移1格。
其中飛數實際上可以取任何整數,為了避免飛數過大造成不必要的影響,這里人為規定飛數f的取值范圍為:
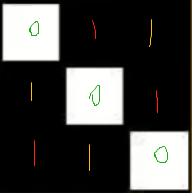
例如:若N1=3時,飛數f的取值為+1、-1、+2、-2;以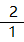
2上1下為例。
( a ) 飛數f=+1
飛數f=+1
( b ) 飛數f=+2
飛數f=+2
( c ) 飛數f=-1
飛數f=-1
( d ) 飛數f=-2
飛數f=-2
不難看出,f=+1和f=-2、f=+2和f=-1所對應的組織圖是一樣的。
+1 = 3 + (-2)、+2 = 3 + (-1)
故可以得出結論: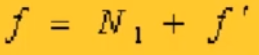
其中f‘為負飛數,f為正飛數;通過這個表達式即可將所有的負飛數均轉化為正數,方便后續的處理。
6,確定第二列矩陣值與第一列矩陣值的關系式
例如: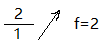 ,
,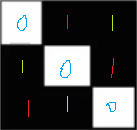
| a[1][1] = 0 | a[1][2]=a[1+2][2-1]=a[3][1]=1 | a[1][3]=a[1+2][3-1]=a[3][2]=1 |
| a[2][1] = 1 | a[2][2]=a[2+2-3][2-1]=a[1][1]=0 | a[2][3]=a[2+2-3][3-1]=a[1][2]=1 |
| a[3][1] = 1 | a[3][2]=a[3+2-3][2-1]=a[2][1]=1 | a[3][3]=a[3+2-3][3-1]=a[2][2]=0 |
由規律可得: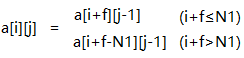 ,其中i=1,2,3,…,m;j=1,2,3…,n;規則組織中m=n。
,其中i=1,2,3,…,m;j=1,2,3…,n;規則組織中m=n。
7,舉例推理驗證:
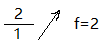
解析:拿到這個分式的時候,先寫出組織的一般形式,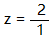 可得:
可得:m=n=1、c1=2、d1=1、f=+2(右斜飛數為正,左斜飛數為負)
( )
)
首先,求解第一列元素值:a[3][1]=1,a[2][1]=1,a[1][1]=0,即
a[3][2]=a[3+2-3][2-1]=a[2][1]=1、a[2][2]=a[2+2-3][2-1]=a[1][1]=0、a[1][2]=a[1+2][2-1]=a[3][1]=1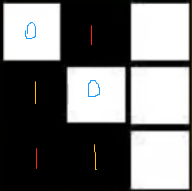
a[3][3]=a[3+2-3][3-1]=a[2][2]=0、a[2][3]=a[2+2-3][3-1]=a[1][2]=1、a[1][3]=a[1+2][3-1]=a[3][2]=1
三、知道組織點對應的矩陣值關系之后,開始編寫程序
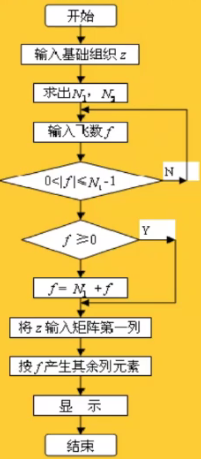
1,規則組織的程序流程圖如下:
2,代碼實現:
#include <iostream>
#include<stdio.h>
using namespace std;int main()
{int i,j,N1,N2,f,m;//因為規則組織是方陣,m=n,故這里只定義m即可int c[10],d[10],a[100][100];//c數組主要存儲c1、c2、c3...,d數組主要存儲d1、d2、d3...printf("please input m:");scanf("%d",&m);//確定矩陣的大小for(i=0;i<m;i++)//依次輸入ci和di的值,其中i∈[0,m),也就總共m個,數組下標從0開始的而已。{printf("please input C[%d]:",i+1);scanf("%d",&c[i]);printf("please input D[%d]:",i+1);scanf("%d",&d[i]);}N1=0;//緯紗循環數初始化,之后需要累加for(i=0;i<=m-1;i++)//確定緯組織循環數,也就是Σ(ci+di),分子分母之和即可{N1=N1+c[i]+d[i];//確定出緯紗循環數N1}N2=N1;//因為是規則組織故其對應的經緯組織循環數相等printf("please input f:");//輸入飛數scanf("%d",&f);if(f<0)f=N1+f;//若飛數為負數,通過公式轉換成正數/*
對第1列進行賦值
*/i=1;//先對第一列賦值,從第一列的第一行開始for(j=0;j<m;j++){while(c[j]>0){a[N1-i+1][1]=1;//因為是分子,所有值都賦值為1c[j]--;//用一次減一次i++;//下一行進行賦值}while(d[j]>0){a[N1-i+1][1]=0;//因為是分母,所有值都賦值為0d[j]--;i++;}}/*
對2到N1列 進行賦值
*/for(j=2;j<=N2;j++){for(i=1;i<=N1;i++){if((i+f)>N1) a[i][j] = a[i+f-N1][j-1];else a[i][j]=a[i+f][j-1];}}/*
輸出二維數組a[i][j]
*/for(i=1;i<=N1;i++){for(j=1;j<=N2;j++){printf("%5d",a[i][j]);}printf("\n");}getchar();//吞一個回車鍵return 0;
}運行效果如下: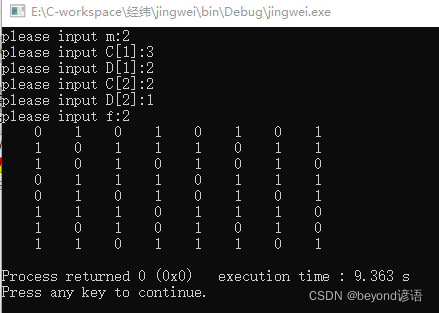

![e-r模型教案高中計算機,《ER模型1》[數據庫][計算機]教案.doc](http://pic.xiahunao.cn/e-r模型教案高中計算機,《ER模型1》[數據庫][計算機]教案.doc)
利用ASP.NET加密和解密Web.config中連接字符串)
方法)





方法與示例)






方法與示例)


