基礎概念公式推到可參考該專欄下的前幾篇博文。
緯向破斜組織圖：
下半部分(從左往右)：
，3上2下2上1下，右斜，飛數為+1
上半部分(從下往上)：
，2上2下1上3下。左斜，飛數為-1
通過分析可得：下半部分即從第N1行到N1-Kw+1行，不管是緯山形組織還是緯向破斜組織都是一樣的
不一樣的地方在于上半部分：
對于緯山形組織而言，上半部分組織點運動規律不變；
但是對于緯向破斜組織而言，上下部分組織點運動規律不一樣。
一、確定經緯紗循環數N2和N1
由于上下兩部分是完全反對稱關系，故N1= 2 * Kw
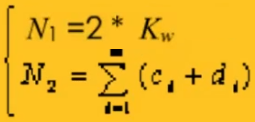
二、對矩陣中最下面的一行(N1行)進行賦值
對于一個矩陣而言其大小為N1行N2列，并且組織中的行數是從上而下進行排列，即第一根緯紗對應的就是N1行。
緯山形N1行的求法與經山形的第一列求法一致，取分子是1，分母為0。
對于N1行的任意一個元素可以標識為a[N1][j]，j=1,2,3,…,N2。
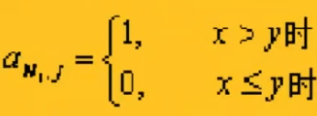，其中j=1,2,3,…,N2
三、根據 N1 行求 N1 - 1到N1 - Kw + 1行，即求下半部分的右斜組織
，其中i=N1-1,N1-2,…,N1-kw+1；j=1,2,3,…,N2
四、根據N1 - Kw + 1行對N1 - Kw行進行求解，即上半部分左斜組織的最下面一行，不管是經向破斜組織還是緯向破斜組織上下兩部分都是反對稱關系，根據這個特點可以把N1 - Kw行元素確定出來
其中j=1,2,3,…,N2
五、根據對N1 - Kw行元素即可對上半部分的組織進行求解，注意飛數需要改變一下即可
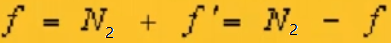
其中j=1,2,3,…,N2
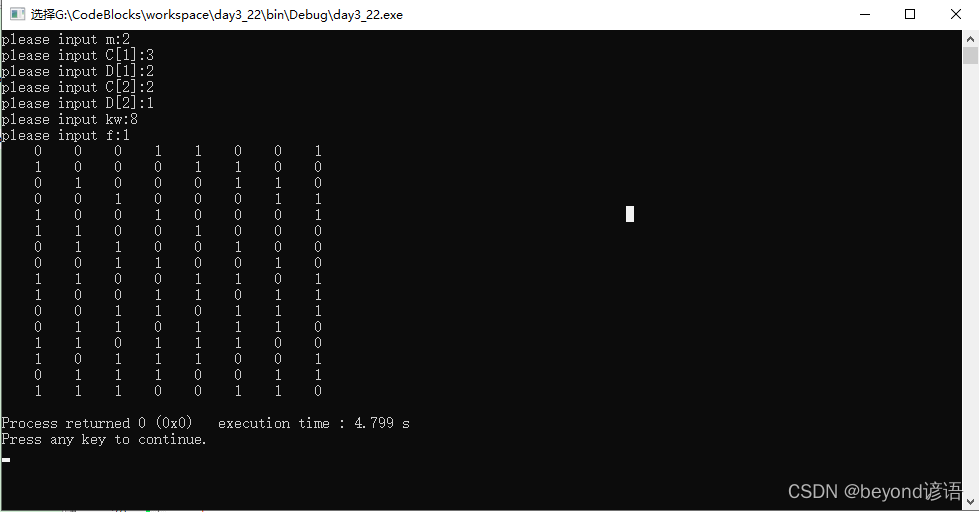
代碼如下:
#include <iostream>
#include<stdio.h>
using namespace std;int main()
{int i,j,N1,N2,f,m,kw;//kw表示山峰的位置，從而確定出總列數N1int c[10],d[10],a[100][100];printf("please input m:");scanf("%d",&m);for(i=0;i<=m-1;i++){printf("please input C[%d]:",i+1);scanf("%d",&c[i]);printf("please input D[%d]:",i+1);scanf("%d",&d[i]);}printf("please input kw:");scanf("%d",&kw);//輸入山峰位置，從而確定出總行數N2=0;//列數初始化，即經紗循環數初始化，之后需要累加for(i=0;i<=m-1;i++){N2=N2+c[i]+d[i];}N1=2*kw;//總行數printf("please input f:");scanf("%d",&f);/*
對第N1行進行賦值
*/j=1;//先對N1行賦值，從N1行的第1列開始for(i=0;i<=m-1;i++){while(c[i]>0){a[N1][j]=1;//因為是分子，所有值都賦值為1c[i]--;j++;}while(d[i]>0){a[N1][j]=0;//因為是分母，所有值都賦值為0d[i]--;j++;}}/*
對N1-1到N1-kw+1行，進行賦值
*/for(i=N1-1;i>=N1-kw+1;i--){for(j=1;j<=N2;j++){if((j-f)>0) a[i][j] = a[i+1][j-f];else a[i][j]=a[i+1][j-f+N2];}}/*
根據N1-kw+1行 對 N1-kw行進行賦值
*/for(j=1;j<=N2;j++){if(a[N1-kw+1][j]==0)a[N1-kw][j]=1;elsea[N1-kw][j]=0;}f=N2-f;//保證飛數為正數/*
對N1-kw-1行到第1行，進行賦值
*/for(i=N1-kw-1;i>=1;i--){for(j=1;j<=N2;j++){if((j-f)>0) a[i][j] = a[i+1][j-f];else a[i][j]=a[i+1][j-f+N2];}}/*
輸出二維數組a[i][j]
*/for(i=1;i<=N1;i++){for(j=1;j<=N2;j++){printf("%5d",a[i][j]);}printf("\n");}getchar();return 0;
}
