伙伴分配器的一個極簡實現

提起buddy system相信很多人不會陌生，它是一種經典的內存分配算法，大名鼎鼎的Linux底層的內存管理用的就是它。這里不探討內核這么復雜實現，而僅僅是將該算法抽象提取出來，同時給出一份及其簡潔的源碼實現，以便定制擴展。

伙伴分配的實質就是一種特殊的“分離適配”，即將內存按2的冪進行劃分，相當于分離出若干個塊大小一致的空閑鏈 表，搜索該鏈表并給出同需求最佳匹配的大小。其優點是快速搜索合并（O(logN)時間復雜度）以及低外部碎片（最佳適配best-fit）；其缺點是內 部碎片，因為按2的冪劃分塊，如果碰上66單位大小，那么必須劃分128單位大小的塊。但若需求本身就按2的冪分配，比如可以先分配若干個內存池，在其基 礎上進一步細分就很有吸引力了。

可以在維基百科上找到該算法的描述，大體如是：

分配內存：

1.尋找大小合適的內存塊（大于等于所需大小并且最接近2的冪，比如需要27，實際分配32）

1. .如果找到了，分配給應用程序。
2. 如果沒找到，分出合適的內存塊。
   1. .對半分離出高于所需大小的空閑內存塊
   2. .如果分到最低限度，分配這個大小。
   3. 回溯到步驟1（尋找合適大小的塊）
   4. .重復該步驟直到一個合適的塊

?

釋放內存：

1.釋放該內存塊

1. 尋找相鄰的塊，看其是否釋放了。
2. 如果相鄰塊也釋放了，合并這兩個塊，重復上述步驟直到遇上未釋放的相鄰塊，或者達到最高上限（即所有內存都釋放了）。

上面這段文字對你來說可能看起來很費勁，沒事，我們看個內存分配和釋放的示意圖你就知道了：

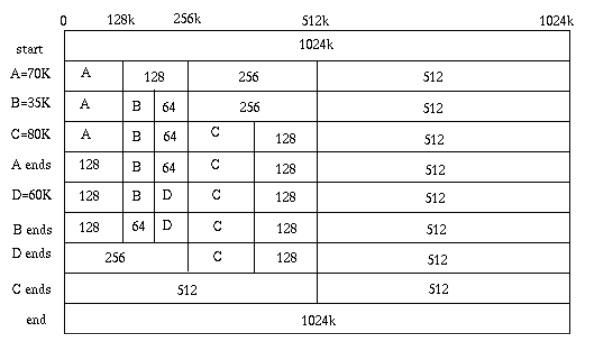
上圖中，首先我們假設我們一個內存塊有1024K，當我們需要給A分配70K內存的時候，

1. 我們發現1024K的一半大于70K，然后我們就把1024K的內存分成兩半，一半512K。
2. 然后我們發現512K的一半仍然大于70K，于是我們再把512K的內存再分成兩半，一半是128K。
3. 此時，我們發現128K的一半小于70K，于是我們就分配為A分配128K的內存。

后面的，B，C，D都這樣，而釋放內存時，則會把相鄰的塊一步一步地合并起來（合并也必需按分裂的逆操作進行合并）。

我們可以看見，這樣的算法，用二叉樹這個數據結構來實現再合適不過了。

我在網上分別找到cloudwu和wuwenbin寫的兩份開源實現和測試用例。實際上后一份是對前一份的精簡和優化，本文打算從后一份入手講解，因為這份實現真正體現了“極簡”二字，追求突破常規的，極致簡單的設計。網友對其評價甚高，甚至可用作教科書標準實現，看完之后回過頭來看cloudwu的代碼就容易理解了。

分配器的整體思想是，通過一個數組形式的完全二叉樹來監控管理內存，二叉樹的節點用于標記相應內存塊的使用狀態，高層節點對應大的塊，低層節點對應 小的塊，在分配和釋放中我們就通過這些節點的標記屬性來進行塊的分離合并。如圖所示，假設總大小為16單位的內存，我們就建立一個深度為5的滿二叉樹，根 節點從數組下標[0]開始，監控大小16的塊；它的左右孩子節點下標[1~2]，監控大小8的塊；第三層節點下標[3~6]監控大小4的塊……依此類推。

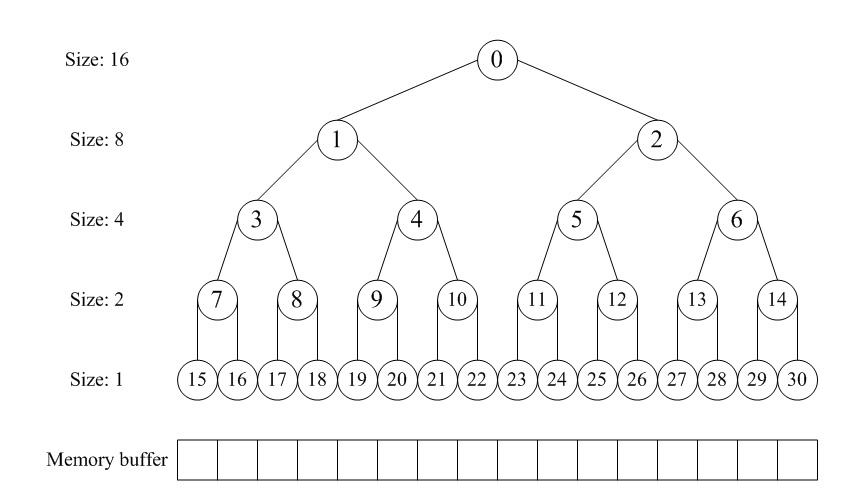
在分配階段，首先要搜索大小適配的塊，假設第一次分配3，轉換成2的冪是4，我們先要對整個內存進行對半切割，從16切割到4需要兩步，那么從下標 [0]節點開始深度搜索到下標[3]的節點并將其標記為已分配。第二次再分配3那么就標記下標[4]的節點。第三次分配6，即大小為8，那么搜索下標 [2]的節點，因為下標[1]所對應的塊被下標[3~4]占用了。

在釋放階段，我們依次釋放上述第一次和第二次分配的塊，即先釋放[3]再釋放[4]，當釋放下標[4]節點后，我們發現之前釋放的[3]是相鄰的， 于是我們立馬將這兩個節點進行合并，這樣一來下次分配大小8的時候，我們就可以搜索到下標[1]適配了。若進一步釋放下標[2]，同[1]合并后整個內存 就回歸到初始狀態。

還是看一下源碼實現吧，首先是伙伴分配器的數據結構：

struct?buddy2?{?
??unsigned?size;?
??unsigned?longest[1];?
};?

這里的成員size表明管理內存的總單元數目（測試用例中是32），成員longest就是二叉樹的節點標記，表明所對應的內存塊的空閑單位，在下文中會分析這是整個算法中最精妙的設計。此處數組大小為1表明這是可以向后擴展的（注：在GCC環境下你可以寫成longest[0]，不占用空間，這里是出于可移植性考慮），我們在分配器初始化的buddy2_new可以看到這種用法。

truct?buddy2*?buddy2_new(?int?size?)?{?
??struct?buddy2*?self;?
??unsigned?node_size;?
??int?i;?
??
??if?(size?<?1?||?!IS_POWER_OF_2(size))?
????return?NULL;?
??
??self?=?(struct?buddy2*)ALLOC(?2?*?size?*?sizeof(unsigned));?
??self->size?=?size;?
??node_size?=?size?*?2;?
??
??for?(i?=?0;?i?<?2?*?size?-?1;?++i)?{?
????if?(IS_POWER_OF_2(i+1))?
??????node_size?/=?2;?
????self->longest[i]?=?node_size;?
??}?
??return?self;?
}?

整個分配器的大小就是滿二叉樹節點數目，即所需管理內存單元數目的2倍。一個節點對應4個字節，longest記錄了節點所對應的的內存塊大小。

內存分配的alloc中，入參是分配器指針和需要分配的大小，返回值是內存塊索引。alloc函數首先將size調整到2的冪大小，并檢查是否超過最大限度。然后進行適配搜索，深度優先遍歷，當找到對應節點后，將其longest標記為0，即分離適配的塊出來，并轉換為內存塊索引offset返回，依據二叉樹排列序號，比如內存總體大小32，我們找到節點下標[8]，內存塊對應大小是4，則offset = (8+1)*4-32 = 4，那么分配內存塊就從索引4開始往后4個單位。

int?buddy2_alloc(struct?buddy2*?self,?int?size)?{?
??unsigned?index?=?0;?
??unsigned?node_size;?
??unsigned?offset?=?0;?
??
??if?(self==NULL)?
????return?-1;?
??
??if?(size?<=?0)?
????size?=?1;?
??else?if?(!IS_POWER_OF_2(size))?
????size?=?fixsize(size);?
??
??if?(self->longest[index]?<?size)?
????return?-1;?
??
??for(node_size?=?self->size;?node_size?!=?size;?node_size?/=?2?)?{?
????if?(self->longest[LEFT_LEAF(index)]?>=?size)?
??????index?=?LEFT_LEAF(index);?
????else?
??????index?=?RIGHT_LEAF(index);?
??}?
??
??self->longest[index]?=?0;?
??offset?=?(index?+?1)?*?node_size?-?self->size;?
??
??while?(index)?{?
????index?=?PARENT(index);?
????self->longest[index]?=?
??????MAX(self->longest[LEFT_LEAF(index)],?self->longest[RIGHT_LEAF(index)]);?
??}?
??
??return?offset;?
}?

在函數返回之前需要回溯，因為小塊內存被占用，大塊就不能分配了，比如下標[8]標記為0分離出來，那么其父節點下標[0]、[1]、[3]也需要相應大小的分離。將它們的longest進行折扣計算，取左右子樹較大值，下標[3]取4，下標[1]取8，下標[0]取16，表明其對應的最大空閑值。

在內存釋放的free接口，我們只要傳入之前分配的內存地址索引，并確保它是有效值。之后就跟alloc做反向回溯，從最后的節點開始一直往上找到longest為0的節點，即當初分配塊所適配的大小和位置。我們將longest恢復到原來滿狀態的值。繼續向上回溯，檢查是否存在合并的塊，依據就是左右子樹longest的值相加是否等于原空閑塊滿狀態的大小，如果能夠合并，就將父節點longest標記為相加的和（多么簡單！）。

void?buddy2_free(struct?buddy2*?self,?int?offset)?{?
??unsigned?node_size,?index?=?0;?
??unsigned?left_longest,?right_longest;?
??
??assert(self?&&?offset?>=?0?&&?offset?<?size);?
??
??node_size?=?1;?
??index?=?offset?+?self->size?-?1;?
??
??for?(;?self->longest[index]?;?index?=?PARENT(index))?{?
????node_size?*=?2;?
????if?(index?==?0)?
??????return;?
??}?
??
??self->longest[index]?=?node_size;?
??
??while?(index)?{?
????index?=?PARENT(index);?
????node_size?*=?2;?
??
????left_longest?=?self->longest[LEFT_LEAF(index)];?
????right_longest?=?self->longest[RIGHT_LEAF(index)];?
??
????if?(left_longest?+?right_longest?==?node_size)?
??????self->longest[index]?=?node_size;?
????else?
??????self->longest[index]?=?MAX(left_longest,?right_longest);?
??}?
}?

上面兩個成對alloc/free接口的時間復雜度都是O(logN)，保證了程序運行性能。然而這段程序設計的獨特之處就在于使用加權來標記內存空閑狀態，而不是一般的有限狀態機，實際上longest既可以表示權重又可以表示狀態，狀態機就毫無必要了，所謂“少即是多”嘛！反 觀cloudwu的實現，將節點標記為UNUSED/USED/SPLIT/FULL四個狀態機，反而會帶來額外的條件判斷和管理實現，而且還不如數值那 樣精確。從邏輯流程上看，wuwenbin的實現簡潔明了如同教科書一般，特別是左右子樹的走向，內存塊的分離合并，塊索引到節點下標的轉換都是一步到 位，不像cloudwu充斥了大量二叉樹的深度和長度的間接計算，讓代碼變得晦澀難讀，這些都是longest的功勞。一個“極簡”的設計往往在于你想不到的突破常規思維的地方。

這份代碼唯一的缺陷就是longest的大小是4字節，內存消耗大。但cloudwu的博客上有人提議用logN來保存值，這樣就能實現uint8_t大小了，看，又是一個“極簡”的設計！

說實話，很難在網上找到比這更簡約更優雅的buddy system實現了——至少在Google上如此。

原文鏈接：

譯文鏈接：