目錄

• 二分法細節
• 1、leetcode 34 在排序數組中查找元素的第一個和最后一個位置
• 2、不完全有序下的二分查找(leetcode33. 搜索旋轉排序數組)
• 3、含重復元素的不完全有序下的二分查找(81. 搜索旋轉排序數組 II)
• 3、不完全有序下的找最小元素(153. 尋找旋轉排序數組中的最小值)
• 4、二維矩陣二分(74. 搜索二維矩陣)

二分法細節

1、計算mid時，不能使用(left + right)/2,否則有可能計算溢出。
可以使用下面方法計算：

mid = left + ((right - left) >> 1)

2、while(left <= right)，注意符號為 <=
如果是 left < right，則當我們執行到最后一步，left與right重疊時，則會跳出循環。但是事實是，此時的left和right指向的可能就是我們的目標元素。
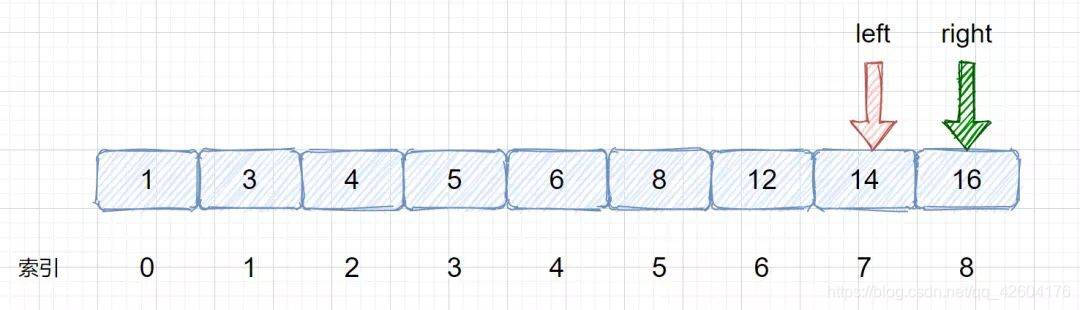
3、 left = mid + 1,right = mid - 1;
如果設置left = mid ，right = mid,left=1,right = 8，mid = 7，會陷入死循環，mid一直為7.

1、leetcode 34 在排序數組中查找元素的第一個和最后一個位置

https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/
在普通的二分上加上檢索區間的左右邊界，需要注意特殊的輸入情況。

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if(nums.empty()) return{-1,-1};int left = 0;int right = nums.size() - 1;while(left <= right){int mid = left + ((right - left) >> 1);if(nums[mid] == target){int l = mid;int r = mid;//尋找左邊界//尋找右邊界while( l >= 0 && nums[l] == target) l--;while(r <= nums.size() - 1 && nums[r] == target) r++;l += 1;r -= 1;if(l < 0) l = 0;if(r > nums.size() - 1) r = nums.size() - 1;return {l,r};}else if(nums[mid] > target){right = mid -1;}else{left = mid + 1;}}return {-1,-1};}
};

2、不完全有序下的二分查找(leetcode33. 搜索旋轉排序數組)

https://leetcode-cn.com/problems/search-in-rotated-sorted-array/
升序排列的整數數組 nums 在預先未知的某個點上進行了旋轉（例如， [0,1,2,4,5,6,7] 經旋轉后可能變為 [4,5,6,7,0,1,2] ）。

請你在數組中搜索 target ，如果數組中存在這個目標值，則返回它的索引，否則返回 -1 。
注意這里的數組中不包含重復的元素。
示例 1：

輸入：nums = [4,5,6,7,0,1,2], target = 0
輸出：4

示例 2：

輸入：nums = [4,5,6,7,0,1,2], target = 3
輸出：-1

示例 3：

輸入：nums = [1], target = 0
輸出：-1

之前使用的二分都是在數組是有序的背景下，如果不完全有序時也是可以使用二分查找的。
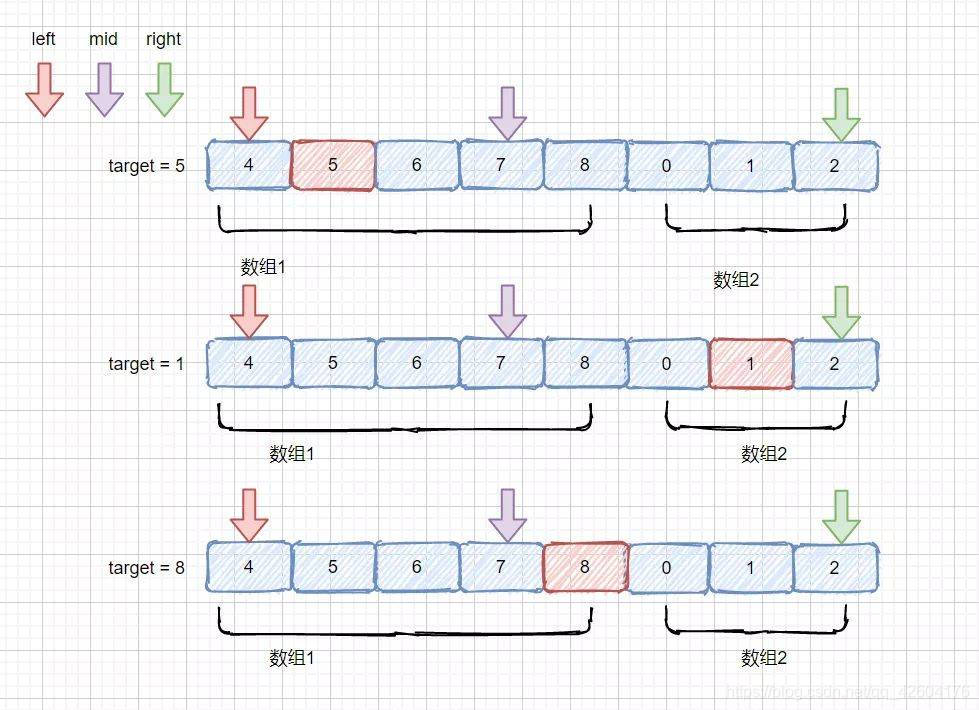
已知分開來的兩個子數組都是有序遞增的。那么如果nums[mid]>= nums[left]則說明mid和left一定落在同一個子數組里，反之nums[mid]< nums[left],說明mid和left不在同一個子數組里，并且此時可以肯定left在數組1，mid在數組2。
注意這里的mid還是通過left和right的下標來求得的，也就是說mid還是在left與right之間。
如果mid和left在同一個子數組中，那么target一共有2種分布的可能：
1、target在mid左邊，此時有target >= nums[left] && target < nums[mid],令right = mid - 1，這樣就在有序的數組1中進行尋找了
2、target在mid右邊，此時有 target > nums[mid] || target < nums[left],令left = mid + 1,緩慢地將left和right指針驅趕到同一個有序區間內。

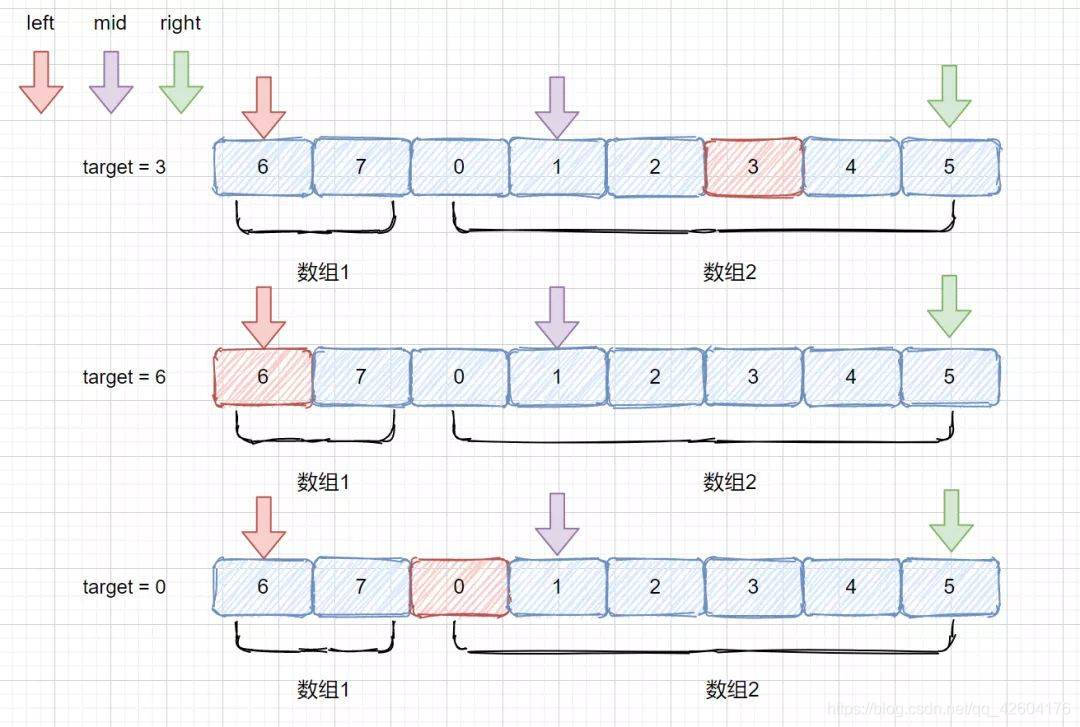
如果mid和right在同一個子數組中，那么target一共有2種分布的可能：
1、target <= nums[right] && target > nums[mid]
此時查找部分就落在右半部分，令left= mid + 1，這樣就在有序的數組2中進行尋找了
2、target > nums[right] || target < nums[mid]
此時mid落在左半部分，應該令right = mid - 1,將兩個指針驅趕到同一個有序區間內

AC代碼

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;while(left <= right){int mid = left + ((right - left) >> 1);if(nums[mid] == target){return mid;}//left and mid 落在同一個數組if(nums[mid] >= nums[left]){//mid和left一個數組,target在左邊數組if(target >= nums[left] && target < nums[mid]){right = mid - 1;}//mid和right一個數組else if(target > nums[mid] || target < nums[left]){left = mid + 1;}}//left and mid 落在不同數組else if(nums[mid] < nums[left]){//target在mid 和 right之間if(nums[mid] < target && target <= nums[right]){left = mid + 1;}//target在left 和mid之間else if(target > nums[right] || target < nums[mid]){right = mid - 1;}}}//沒有查找到return -1;}
};

這一題思路還是比較麻煩的，不易想到，還需要加深理解才行。

3、含重復元素的不完全有序下的二分查找(81. 搜索旋轉排序數組 II)

https://leetcode-cn.com/problems/search-in-rotated-sorted-array-ii/
假設按照升序排序的數組在預先未知的某個點上進行了旋轉。

( 例如，數組 [0,0,1,2,2,5,6] 可能變為 [2,5,6,0,0,1,2] )。

編寫一個函數來判斷給定的目標值是否存在于數組中。若存在返回 true，否則返回 false。

示例 1:

輸入: nums = [2,5,6,0,0,1,2], target = 0
輸出: true

示例 2:

輸入: nums = [2,5,6,0,0,1,2], target = 3
輸出: false

進階:
這是 搜索旋轉排序數組 的延伸題目，本題中的 nums 可能包含重復元素。
這會影響到程序的時間復雜度嗎？會有怎樣的影響，為什么？
如果我們直接套用之前的思路會發現出現下面的問題：

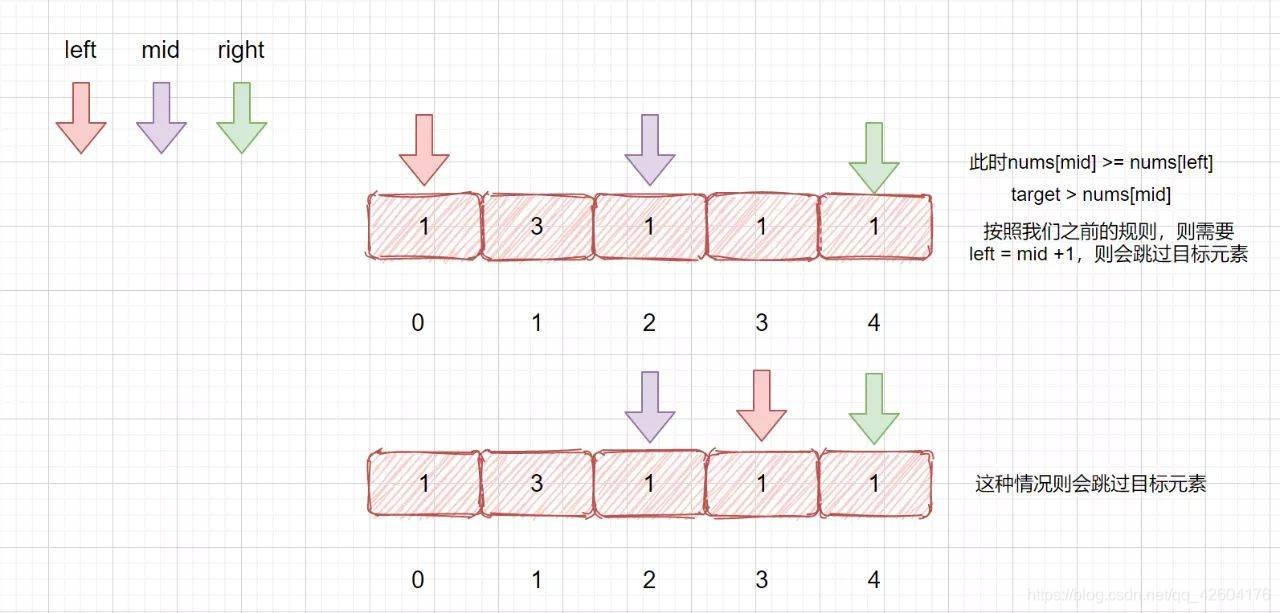
原因就是nums[left] == nums[mid]時，這里可能會有問題。
這時我們需要讓left++即可。注意在書寫代碼的時候我們需要在left++后這次循環就結束，所以我們把nums[left] == nums[mid]的情況放到最后處理即可：

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1;while(left <= right){int mid = left + ((right - left) >> 1);if(nums[mid] == target){return true;}//left and mid 落在同一個數組if(nums[mid] > nums[left]){//mid和left一個數組,target在左邊數組if(target >= nums[left] && target < nums[mid]){right = mid - 1;}//mid和right一個數組else if(target > nums[mid] || target < nums[left]){left = mid + 1;}}//left and mid 落在不同數組else if(nums[mid] < nums[left]){//target在mid 和 right之間if(nums[mid] < target && target <= nums[right]){left = mid + 1;}//target在left 和mid之間else if(target > nums[right] || target < nums[mid]){right = mid - 1;}}elseleft++;}//沒有查找到return false;}
};

3、不完全有序下的找最小元素(153. 尋找旋轉排序數組中的最小值)

https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/
假設按照升序排序的數組在預先未知的某個點上進行了旋轉。例如，數組 [0,1,2,4,5,6,7] 可能變為 [4,5,6,7,0,1,2] 。

請找出其中最小的元素。
示例 1：

輸入：nums = [3,4,5,1,2]
輸出：1

示例 2：

輸入：nums = [4,5,6,7,0,1,2]
輸出：0

示例 3：

輸入：nums = [1]
輸出：1

由于跳變點小于左邊的值，大于右邊的值。所以當nums[mid] < nums[left]時，說明跳變點在mid與left之間，因為mid與right之間必然是遞增的（跳變只有一次）。
當nums[mid] > nums[left]說明mid與left之間是單調遞增的。
當nums[mid] == nums[left]說明此時mid與left重合了,此時需要將left向右移動1格，然后重新迭代。

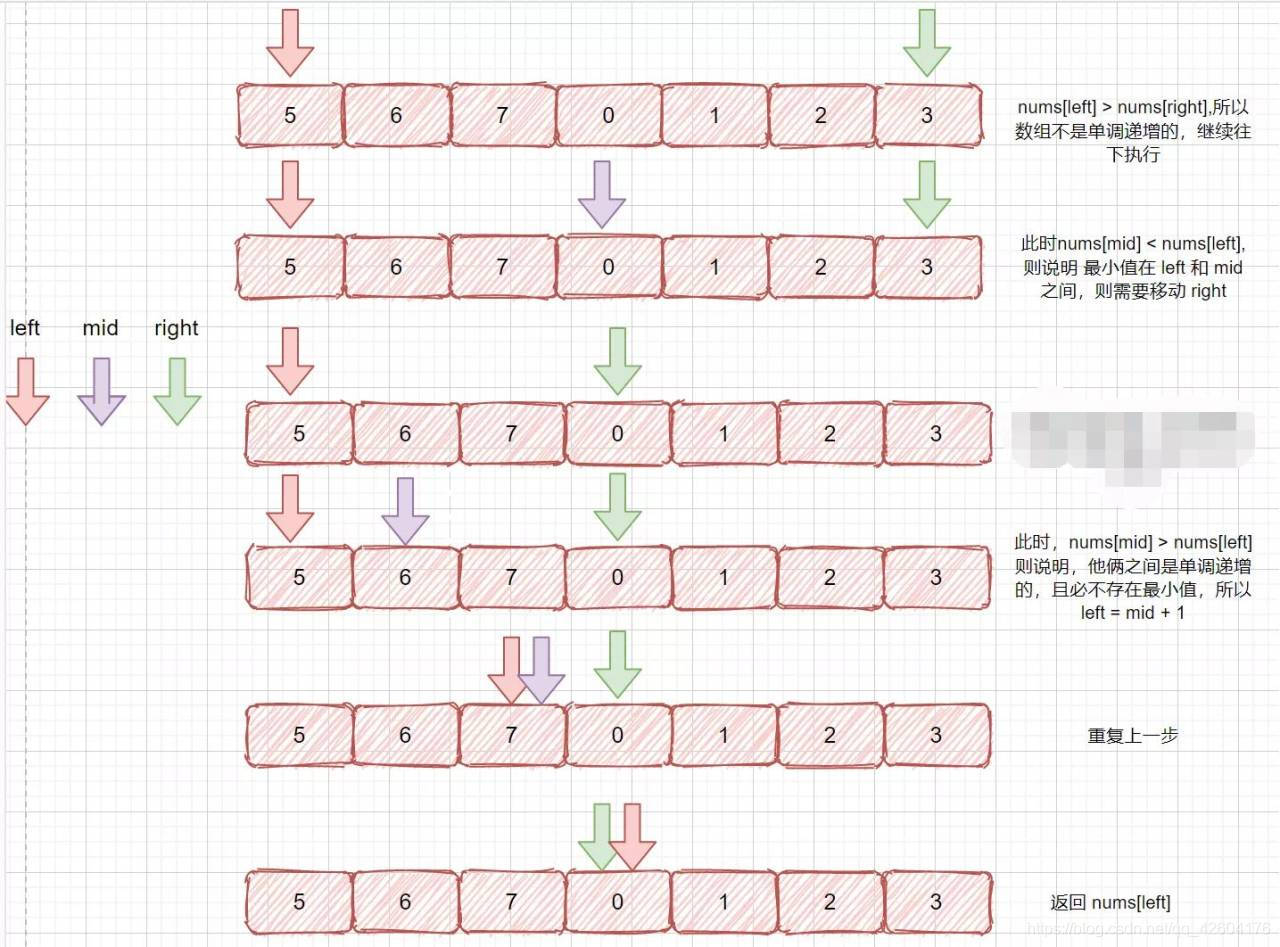
class Solution {
public:int findMin(vector<int>& nums) {if(nums.size() == 1) return nums[0];int left = 0;int right = nums.size() - 1;while(left <= right){if(nums[left] <= nums[right]) return nums[left];int mid = left + ((right - left) >> 1);if(nums[mid] < nums[left]) right = mid;else if(nums[mid] > nums[left]) left = mid + 1;else if(left == mid) left++;}return -1;}
};

4、二維矩陣二分(74. 搜索二維矩陣)

https://leetcode-cn.com/problems/search-a-2d-matrix/
編寫一個高效的算法來判斷 m x n 矩陣中，是否存在一個目標值。該矩陣具有如下特性：

每行中的整數從左到右按升序排列。
每行的第一個整數大于前一行的最后一個整數。
示例 1：

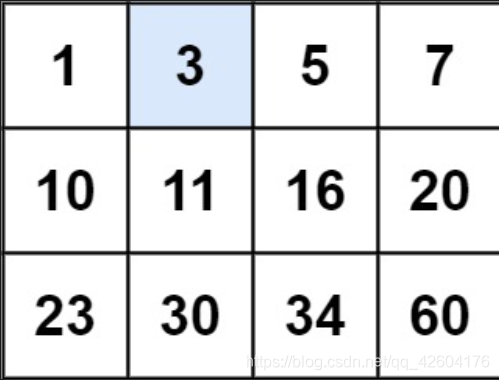
輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
輸出：true

示例 2：

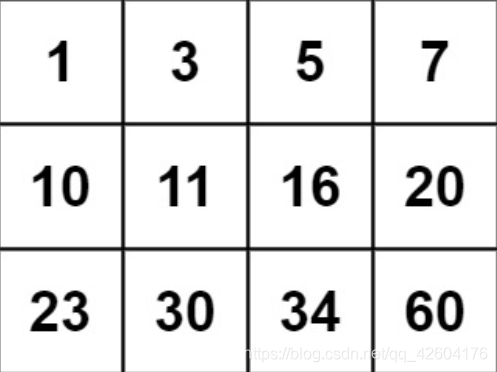
輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
輸出：false

示例 3：

輸入：matrix = [], target = 0
輸出：false

只要將二維數組展開成一維數組即可，用普通的二分。
需要注意的是將mid轉換成行列坐標;

mid/col 得到的是行數
mid % col 得到的是列數

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {//獲得行數int row = matrix.size();if(row == 0) return false;//獲得列數int col = matrix[0].size();int left = 0;int right = row * col - 1;while(left <= right){int mid = left + ((right - left) >> 1);if(target == matrix[mid/col][mid%col]) return true;else if(target > matrix[mid/col][mid%col]) left = mid + 1;else right = mid - 1;}return false;}
};