目錄
1、紅黑樹原理
1、紅黑樹性質
2、變換規則（從插入結點的角度來講）
1.變色
2.左旋
3.右旋
3、刪除結點需要注意的地方
2、代碼
1、定義結點以及構造函數
2、定義紅黑樹類以及聲明它的方法
3、左旋
4、右旋
5、插入操作
6、修正操作
7、刪除操作
3、參考鏈接

1、紅黑樹原理

為了避免二叉搜索樹出現退化為鏈表的情況，出現了自平衡的二叉搜索樹。
AVL樹：平衡二叉樹，它的左右子樹高度之差不超過1，不過它太過于理想化。
通過性能綜合考慮選用紅黑樹。

1、紅黑樹性質

1、每個結點不是紅色就是黑色
2、不可能有連在一起的紅色結點
3、根結點都是黑色
4、每個紅色結點的兩個子結點都是黑色。
5、葉子結點都是黑色(葉子結點指的是NULL結點)
6、從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。

2、變換規則（從插入結點的角度來講）

變換規則分為三種：

變色、左旋、右旋

1.變色

變色的前提：當前結點的父結點是紅色，且它的祖父結點的另一個結點==(叔結點)也是紅色==。
變色的過程：

1、將父結點設為黑色
2、叔結點設為黑色
3、祖父結點設為紅色
4、把指針定義到祖父結點設為當前要操作的結點。
5、繼續分析判斷

示例如下：
按照二叉搜索樹的規則插入對應的結點6；發現違反規則了，兩個紅色的連到一起了，并且符合變色的前提，所以進行變色

圖1 插入結點6，將其作為當前結點

圖2 做完變色變換后，將之前的祖父結點作為當前結點

2.左旋

觀察變色之后的樹，發現仍然是違反規則的：5、12兩個紅色連在一起了。
然后再看是不是符合變色的前提：顯然不符合，因為12的叔結點30不是紅色。那么這時就應該判斷是否符合左旋的前提了。
左旋的前提：
當前父結點是紅色，叔叔是黑色的時候，且當前的結點是右子樹。
左旋的過程：

以父結點作為中心旋轉，動態圖如下：
1、將當前以當前結點為根結點的子樹(between E and S)連接到祖父結點E
2、E和S中較大的結點作為移動到根結點

左旋前后對比：

圖1 左旋前

圖2 左旋后

3.右旋

觀察左旋之后的樹，發現仍然是違反規則的：5、12兩個紅色的結點連在一起。且不符合變色和左旋的條件。
那么接下來就要使用右旋
右旋條件：
當前父結點是紅色，叔結點是黑色，且當前的結點是左子樹。
右旋的操作：

1、把父結點變為黑色
2、把祖父結點變為紅色
3、以祖父結點旋轉

右旋前后對比;13重新連接。

圖1 右旋前

圖2 右旋后

3、刪除結點需要注意的地方

1、將紅黑樹當做一棵二叉搜索樹，將該結點從二叉搜索樹中刪除
2、通過旋轉和變色操作來修正這棵樹，使之重新成為一棵紅黑樹
關于二叉搜索樹的刪除結點不是這篇筆記的重點，可以參考我之前的一個刷題筆記，還是比較有用處的：

二叉搜索樹的插入、刪除、修剪、構造操作（leetcode701、450、669、108）

怕麻煩的話也可以直接看下面的截圖：
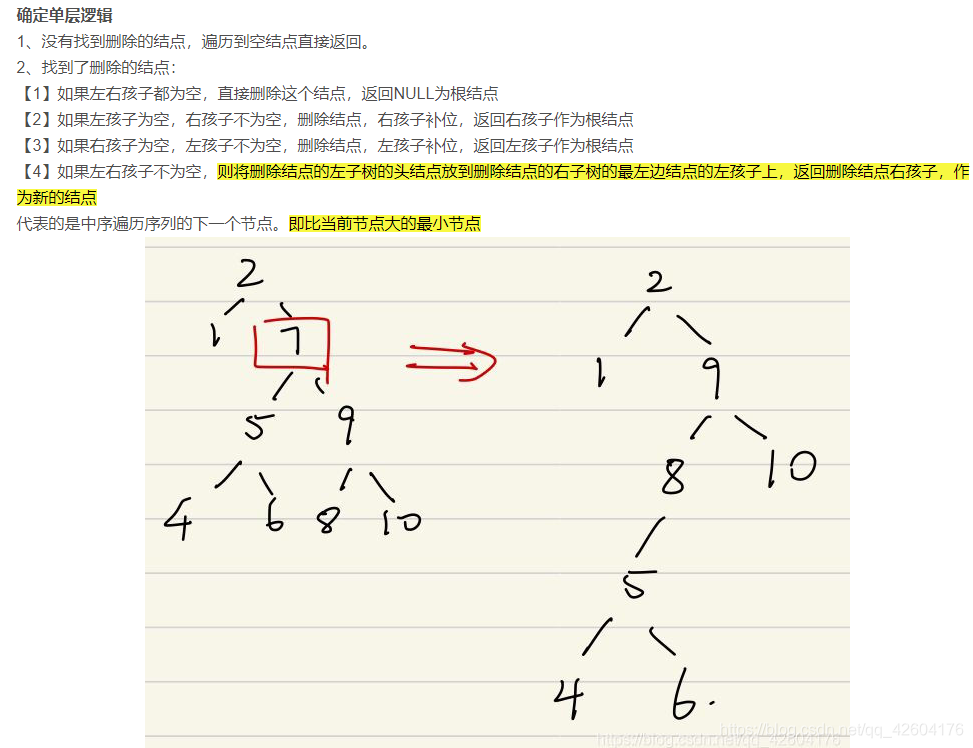
在這里插入圖片描述

2、代碼

1、定義結點以及構造函數

每個結點有顏色和值，左右孩子以及父結點指針。
定義帶參構造函數

template <class T>
class RBTNode{public:RBTColor color;    // 顏色T key;            // 關鍵字(鍵值)RBTNode *left;    // 左孩子RBTNode *right;    // 右孩子RBTNode *parent; // 父結點RBTNode(T value, RBTColor c, RBTNode *p, RBTNode *l, RBTNode *r):key(value),color(c),parent(),left(l),right(r) {}
};

2、定義紅黑樹類以及聲明它的方法

每棵樹有一個根結點還有空結點

template <class T>
class RBTree {private:RBTNode<T> *mRoot;    // 根結點public:RBTree();~RBTree();// 前序遍歷"紅黑樹"void preOrder();// 中序遍歷"紅黑樹"void inOrder();// 后序遍歷"紅黑樹"void postOrder();// (遞歸實現)查找"紅黑樹"中鍵值為key的節點RBTNode<T>* search(T key);// (非遞歸實現)查找"紅黑樹"中鍵值為key的節點RBTNode<T>* iterativeSearch(T key);// 查找最小結點：返回最小結點的鍵值。T minimum();// 查找最大結點：返回最大結點的鍵值。T maximum();// 找結點(x)的后繼結點。即，查找"紅黑樹中數據值大于該結點"的"最小結點"。RBTNode<T>* successor(RBTNode<T> *x);// 找結點(x)的前驅結點。即，查找"紅黑樹中數據值小于該結點"的"最大結點"。RBTNode<T>* predecessor(RBTNode<T> *x);// 將結點(key為節點鍵值)插入到紅黑樹中void insert(T key);// 刪除結點(key為節點鍵值)void remove(T key);// 銷毀紅黑樹void destroy();// 打印紅黑樹void print();private:// 前序遍歷"紅黑樹"void preOrder(RBTNode<T>* tree) const;// 中序遍歷"紅黑樹"void inOrder(RBTNode<T>* tree) const;// 后序遍歷"紅黑樹"void postOrder(RBTNode<T>* tree) const;// (遞歸實現)查找"紅黑樹x"中鍵值為key的節點RBTNode<T>* search(RBTNode<T>* x, T key) const;// (非遞歸實現)查找"紅黑樹x"中鍵值為key的節點RBTNode<T>* iterativeSearch(RBTNode<T>* x, T key) const;// 查找最小結點：返回tree為根結點的紅黑樹的最小結點。RBTNode<T>* minimum(RBTNode<T>* tree);// 查找最大結點：返回tree為根結點的紅黑樹的最大結點。RBTNode<T>* maximum(RBTNode<T>* tree);// 左旋void leftRotate(RBTNode<T>* &root, RBTNode<T>* x);// 右旋void rightRotate(RBTNode<T>* &root, RBTNode<T>* y);// 插入函數void insert(RBTNode<T>* &root, RBTNode<T>* node);// 插入修正函數void insertFixUp(RBTNode<T>* &root, RBTNode<T>* node);// 刪除函數void remove(RBTNode<T>* &root, RBTNode<T> *node);// 刪除修正函數void removeFixUp(RBTNode<T>* &root, RBTNode<T> *node, RBTNode<T> *parent);// 銷毀紅黑樹void destroy(RBTNode<T>* &tree);// 打印紅黑樹void print(RBTNode<T>* tree, T key, int direction);#define rb_parent(r)   ((r)->parent)
#define rb_color(r) ((r)->color)
#define rb_is_red(r)   ((r)->color==RED)
#define rb_is_black(r)  ((r)->color==BLACK)
#define rb_set_black(r)  do { (r)->color = BLACK; } while (0)
#define rb_set_red(r)  do { (r)->color = RED; } while (0)
#define rb_set_parent(r,p)  do { (r)->parent = (p); } while (0)
#define rb_set_color(r,c)  do { (r)->color = (c); } while (0)
};

3、左旋

/* * 對紅黑樹的節點(x)進行左旋轉** 左旋示意圖(對節點x進行左旋)：*      px                              px*     /                               /*    x                               y                *   /  \      --(左旋)-->           / \                #*  lx   y                          x  ry     *     /   \                       /  \*    ly   ry                     lx  ly  ***/
template <class T>
void RBTree<T>::leftRotate(RBTNode<T>* &root, RBTNode<T>* x)
{// 設置x的右孩子為yRBTNode<T> *y = x->right;// 將 “y的左孩子” 設為 “x的右孩子”；// 如果y的左孩子非空，將 “x” 設為 “y的左孩子的父親”x->right = y->left;if (y->left != NULL)y->left->parent = x;// 將 “x的父親” 設為 “y的父親”y->parent = x->parent;if (x->parent == NULL){root = y;            // 如果 “x的父親” 是空節點，則將y設為根節點}else{if (x->parent->left == x)x->parent->left = y;    // 如果 x是它父節點的左孩子，則將y設為“x的父節點的左孩子”elsex->parent->right = y;    // 如果 x是它父節點的左孩子，則將y設為“x的父節點的左孩子”}// 將 “x” 設為 “y的左孩子”y->left = x;// 將 “x的父節點” 設為 “y”x->parent = y;
}

4、右旋

/* * 對紅黑樹的節點(y)進行右旋轉** 右旋示意圖(對節點y進行左旋)：*            py                               py*           /                                /*          y                                x                  *         /  \      --(右旋)-->            /  \                     #*        x   ry                           lx   y  *       / \                                   / \                   #*      lx  rx                                rx  ry* */
template <class T>
void RBTree<T>::rightRotate(RBTNode<T>* &root, RBTNode<T>* y)
{// 設置x是當前節點的左孩子。RBTNode<T> *x = y->left;// 將 “x的右孩子” 設為 “y的左孩子”；// 如果"x的右孩子"不為空的話，將 “y” 設為 “x的右孩子的父親”y->left = x->right;if (x->right != NULL)x->right->parent = y;// 將 “y的父親” 設為 “x的父親”x->parent = y->parent;if (y->parent == NULL) {root = x;            // 如果 “y的父親” 是空節點，則將x設為根節點}else{if (y == y->parent->right)y->parent->right = x;    // 如果 y是它父節點的右孩子，則將x設為“y的父節點的右孩子”elsey->parent->left = x;    // (y是它父節點的左孩子) 將x設為“x的父節點的左孩子”}// 將 “y” 設為 “x的右孩子”x->right = y;// 將 “y的父節點” 設為 “x”y->parent = x;
}

5、插入操作

內部接口 – insert(root, node)的作用是將"node"節點插入到紅黑樹中。其中，root是根，node是被插入節點。
外部接口 – insert(key)的作用是將"key"添加到紅黑樹中。

/* * 將結點插入到紅黑樹中** 參數說明：*     root 紅黑樹的根結點*     node 插入的結點        // 對應《算法導論》中的node*/
template <class T>
void RBTree<T>::insert(RBTNode<T>* &root, RBTNode<T>* node)
{RBTNode<T> *y = NULL;RBTNode<T> *x = root;// 1. 將紅黑樹當作一顆二叉查找樹，將節點添加到二叉查找樹中。while (x != NULL){y = x;if (node->key < x->key)x = x->left;elsex = x->right;}node->parent = y;if (y!=NULL){if (node->key < y->key)y->left = node;elsey->right = node;}elseroot = node;// 2. 設置節點的顏色為紅色node->color = RED;// 3. 將它重新修正為一顆二叉查找樹insertFixUp(root, node);
}/* * 將結點(key為節點鍵值)插入到紅黑樹中** 參數說明：*     tree 紅黑樹的根結點*     key 插入結點的鍵值*/
template <class T>
void RBTree<T>::insert(T key)
{RBTNode<T> *z=NULL;// 如果新建結點失敗，則返回。if ((z=new RBTNode<T>(key,BLACK,NULL,NULL,NULL)) == NULL)return ;insert(mRoot, z);
}

6、修正操作

根據條件，分別進行變色、左旋、右旋操作，最后再將根結點置為黑色。
對于叔叔結點是組父結點的左孩子還是右孩子需要分類討論。
操作的具體步驟，可以返回上文對比看。
insertFixUp(root, node)的作用是對應"上面所講的第三步"。它是一個內部接口。

/** 紅黑樹插入修正函數** 在向紅黑樹中插入節點之后(失去平衡)，再調用該函數；* 目的是將它重新塑造成一顆紅黑樹。** 參數說明：*     root 紅黑樹的根*     node 插入的結點        // 對應《算法導論》中的z*/
template <class T>
void RBTree<T>::insertFixUp(RBTNode<T>* &root, RBTNode<T>* node)
{RBTNode<T> *parent, *gparent;// 若“父節點存在，并且父節點的顏色是紅色”while ((parent = rb_parent(node)) && rb_is_red(parent)){gparent = rb_parent(parent);//若“父節點”是“祖父節點的左孩子”if (parent == gparent->left){RBTNode<T> *uncle = gparent->right;// Case 1條件：叔叔節點是紅色,此時采用變色if (uncle && rb_is_red(uncle)){rb_set_black(uncle);rb_set_black(parent);rb_set_red(gparent);node = gparent;continue;}// Case 2條件：叔叔是黑色，且當前節點是右孩子,此時采用左旋if (parent->right == node){RBTNode<T> *tmp;leftRotate(root, parent);tmp = parent;parent = node;node = tmp;}// Case 3條件：叔叔是黑色，且當前節點是左孩子,此時采用右旋rb_set_black(parent);rb_set_red(gparent);rightRotate(root, gparent);} else//若“z的父節點”是“z的祖父節點的右孩子”{RBTNode<T> *uncle = gparent->left;// Case 1條件：叔叔節點是紅色if (uncle && rb_is_red(uncle)){rb_set_black(uncle);rb_set_black(parent);rb_set_red(gparent);node = gparent;continue;}// Case 2條件：叔叔是黑色，且當前節點是左孩子if (parent->left == node){RBTNode<T> *tmp;rightRotate(root, parent);tmp = parent;parent = node;node = tmp;}// Case 3條件：叔叔是黑色，且當前節點是右孩子。rb_set_black(parent);rb_set_red(gparent);leftRotate(root, gparent);}}// 將根節點設為黑色rb_set_black(root);
}