Problem Statement:
問題陳述:
Given a matrix of dimension r*c where each cell in the matrix can have values 0, 1 or 2 which has the following meaning:
給定尺寸r * C的矩陣,其中矩陣中的每個單元可以具有其具有以下含義的值0,1或2:
0 : Empty cell
0:空單元格
1 : Cells have fresh oranges
1:細胞有新鮮的橘子
2 : Cells have rotten oranges
2:細胞有爛橘子
So, we have to determine what is the minimum time required to all oranges. A rotten orange at index [i,j] can rot other fresh orange at indexes [i-1,j], [i+1,j], [i,j-1], [i,j+1] (up, down, left and right) in unit time. If it is impossible to rot every orange then simply return -1.
因此,我們必須確定所有橙子所需的最短時間是多少。 索引為[i,j]的爛橙可以使索引為[i-1,j] , [i + 1,j] , [i,j-1] , [i,j + 1]的其他鮮橙腐爛(向上,向下,向左和向右)。 如果不可能腐爛每個橙色,則只需返回-1即可 。
Example:
例:
Input:
2
3 5
2 1 0 2 1 1 0 1 2 1 1 0 0 2 1
Output:
2
Explanation:
說明:
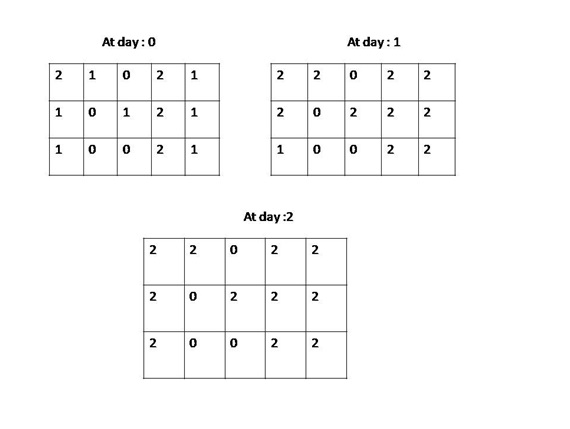
Algorithm:
算法:
To implement this question we use BFS and a queue data structure.
為了解決這個問題,我們使用BFS和隊列 數據結構 。
At first, we push all positions into the queue which has 2 and make a partition by inserting NULL into the queue.
首先,我們將所有位置推入具有2的隊列中,并通過將NULL插入隊列來進行分區。
We pop every element from the queue until the first NULL comes and Go for its four neighbor's if there is any 1 then make it two and push it into the queue and separate this section again inserting a NULL into the queue.
直到第一個NULL來,去它的四個鄰居的,如果有任何1然后將其擴大兩倍,并將它推到隊列中,分離這部分再插入一個NULL值插入到隊列中,我們從隊列中彈出的每一個元素。
Whenever we encounter NULL except for the first NULL and if it is not a last element of the queue then we increase the count value.
每當我們遇到除第一個NULL之外的NULL時,并且如果它不是隊列的最后一個元素,那么我們都會增加計數值。
Repeat step 2 to 3 until the queue is empty.
重復步驟2到3,直到隊列為空。
爛橙問題的C ++實現 (C++ Implementation for Rotten Oranges problem)
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
bool zero(int *arr,int r,int c){
for(int i=0;i<r;i++){
for(int j=0;j<c;j++){
if(*((arr+i*c)+j)==1)
return false;
}
}
return true;
}
int rotten(int *arr,int r,int c){
queue<pair<int,int> >q;
int store=0,temp=0;
for(int i=0;i<r;i++){
for(int j=0;j<c;j++){
if(*((arr+i*c)+j)==2){
q.push(make_pair(i,j));
}
}
}
q.push(make_pair(-1,-1));
while(!q.empty()){
pair<int,int> p=q.front();
q.pop();
if(p.first!=-1){
if(*((arr+p.first*c)+p.second)==1){
temp=1;
*((arr+p.first*c)+p.second)=2;
}
if(p.first==0 && p.second==0){
if(*((arr+(p.first+1)*c)+p.second)==1){
q.push(make_pair((p.first+1),p.second));
}
if(*((arr+(p.first)*c)+p.second+1)==1){
q.push(make_pair((p.first),p.second+1));
}
}
else if(p.first==0 && p.second==c-1){
if(*((arr+(p.first+1)*c)+p.second)==1){
q.push(make_pair((p.first+1),p.second));
}
if(*((arr+(p.first)*c)+p.second-1)==1){
q.push(make_pair((p.first),p.second-1));
}
}
else if(p.first==0){
if(*((arr+(p.first+1)*c)+p.second)==1){
q.push(make_pair((p.first+1),p.second));
}
if(*((arr+(p.first)*c)+p.second-1)==1){
q.push(make_pair((p.first),p.second-1));
}
if(*((arr+(p.first)*c)+p.second+1)==1){
q.push(make_pair((p.first),p.second+1));
}
}
else if(p.first==r-1 && p.second==0){
if(*((arr+(p.first-1)*c)+p.second)==1){
q.push(make_pair((p.first-1),p.second));
}
if(*((arr+(p.first)*c)+p.second+1)==1){
q.push(make_pair((p.first),p.second+1));
}
}
else if(p.second==0){
if(*((arr+(p.first-1)*c)+p.second)==1){
q.push(make_pair((p.first-1),p.second));
}
if(*((arr+(p.first+1)*c)+p.second)==1){
q.push(make_pair((p.first+1),p.second));
}
if(*((arr+(p.first)*c)+p.second+1)==1){
q.push(make_pair((p.first),p.second+1));
}
}
else if(p.first==r-1 && p.second==c-1){
if(*((arr+(p.first-1)*c)+p.second)==1){
q.push(make_pair((p.first-1),p.second));
}
if(*((arr+(p.first)*c)+p.second-1)==1){
q.push(make_pair((p.first),p.second-1));
}
}
else if(p.first==r-1){
if(*((arr+(p.first-1)*c)+p.second)==1){
q.push(make_pair((p.first-1),p.second));
}
if(*((arr+(p.first)*c)+p.second-1)==1){
q.push(make_pair((p.first),p.second-1));
}
if(*((arr+(p.first)*c)+p.second+1)==1){
q.push(make_pair((p.first),p.second+1));
}
}
else if(p.second==c-1){
if(*((arr+(p.first-1)*c)+p.second)==1){
q.push(make_pair((p.first-1),p.second));
}
if(*((arr+(p.first+1)*c)+p.second)==1){
q.push(make_pair((p.first+1),p.second));
}
if(*((arr+(p.first)*c)+p.second-1)==1){
q.push(make_pair((p.first),p.second-1));
}
}
else{
if(*((arr+(p.first)*c)+p.second-1)==1){
q.push(make_pair((p.first),p.second-1));
}
if(*((arr+(p.first)*c)+p.second+1)==1){
q.push(make_pair((p.first),p.second+1));
}
if(*((arr+(p.first-1)*c)+p.second)==1){
q.push(make_pair((p.first-1),p.second));
}
if(*((arr+(p.first+1)*c)+p.second)==1){
q.push(make_pair((p.first+1),p.second));
}
}
}
if(p.first==-1){
if(!q.empty()){
q.push(make_pair(-1,-1));
}
if(temp==1){
store++;
temp=0;
}
}
}
return store;
}
int main() {
int num;
cin>>num;
for(int i=0;i<num;i++){
int r,c;
cin>>r>>c;
int arr[r][c];
for(int j=0;j<r;j++){
for(int k=0;k<c;k++){
cin>>arr[j][k];
}
}
int store=rotten(&arr[0][0],r,c);
if(!zero(&arr[0][0],r,c))
cout<<"-1"<<endl;
else
cout<<store<<endl;
}
return 0;
}
Output
輸出量
Number of days are : 2
翻譯自: https://www.includehelp.com/icp/rotten-oranges.aspx












)






