
難度:困難
題目:
????n?皇后問題研究的是如何將?n?個皇后放置在?n×n?的棋盤上,并且使皇后彼此之間不能相互攻擊。
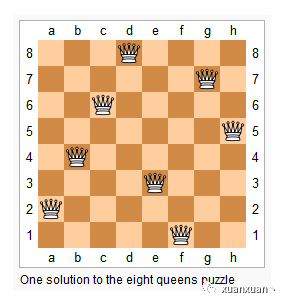
????上圖為 8 皇后問題的一種解法。
????給定一個整數?n,返回?n?皇后不同的解決方案的數量。

提示:
????皇后,是國際象棋中的棋子,意味著國王的妻子。皇后只做一件事,那就是“吃子”。當她遇見可以吃的棋子時,就迅速沖上去吃掉棋子。
????當然,她橫、豎、斜都可走一或 N-1 步,可進可退。(引用自?百度百科 - 皇后?)
--------------------------------------------
??? N皇后問題,經典的題目,記得大學老師很喜歡用來做教學題材,回溯法的入門經典教學用例,8皇后。
????只不過這里不是8皇后,是N個皇后,其實做法都大同小異,只不過一個是寫死8個皇后,一個是支持輸入而已。
??? N皇后問題應該有耳朵的都聽過了吧。
????就是如果當前皇后所在位置,如果上下左右外加 斜上下左右的,已經有存在皇后的話,那就是沖突,就不能放,只能找其他位置。
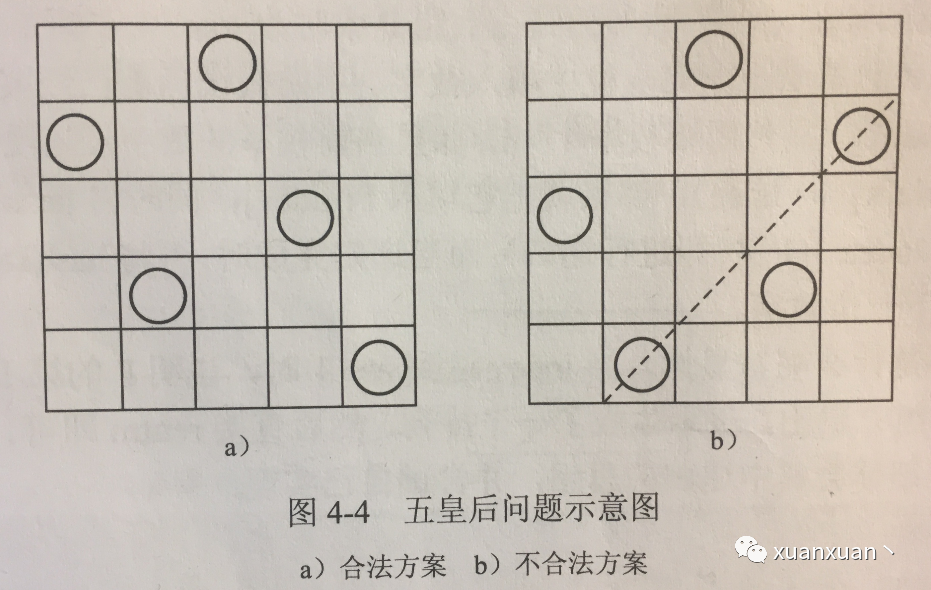
5皇后例子
????如果能找到符合需求的n個皇后都完美放在了棋盤中的話,那就是一個完美的答案,現在需要把所有的答案打印出來,皇后的位置是“Q”,其他空位置為“.”表示。
????這是回溯法的專用教學案例,當然這里也是使用回溯法。
回溯法基本思想就是:
? ??回溯法(探索與回溯法)是一種選優搜索法,又稱為試探法,按選優條件向前搜索,以達到目標。但當探索到某一步時,發現原先選擇并不優或達不到目標,就退回一步重新選擇,這種走不通就退回再走的技術為回溯法,而滿足回溯條件的某個狀態的點稱為“回溯點”。
????其實回溯法在之前的《將數組拆分成斐波那契序列》中也有用到,但是那個還不夠經典。
????歸于當前需求,并結合回溯法思想,也就是找到每行的每一個皇后在哪一列來確定他的坐標[i, j]。
????這里我按列來說。
????從第一列的第一行開始,判斷之前的列有沒沖突,如果有就向下走一格,如果沒有就放下。
????繼續判斷第二列的皇后。
????。????
。
????當到了第n列時,如果這列的皇后放在第x行剛好和之前的沒有沖突,那就是一個答案,然后再向下找(當然已經沒有了,因為每一次到最后一列只有一個答案)。
????那最后一列的已經找到了最后一行了呢,那就來了,回溯。
????退回到前一列(第n-1列),然后前一列的皇后繼續往下面的行移動,如果找到了再繼續后一列(第n列)的判斷。如果沒有就再回溯,回到了n-2列,然后同理的操作。
????當退回到第1列時,全都試探完了,那就是完了。
????這里還可以優化了一下,把二維數組換成了單維數組,i-n和a[i]分別代表行和列。
遞歸實現:
public List> solveNQueens(int n) { List> solutions = new ArrayList>(); int[] queens = new int[n]; Arrays.fill(queens, -1); Set columns = new HashSet(); Set diagonals1 = new HashSet(); Set diagonals2 = new HashSet(); backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2); return solutions;}public void backtrack(List> solutions, int[] queens, int n, int row, Set columns, Set diagonals1, Set diagonals2) { if (row == n) { List board = generateBoard(queens, n); solutions.add(board); } else { for (int i = 0; i < n; i++) { if (columns.contains(i)) { continue; } int diagonal1 = row - i; if (diagonals1.contains(diagonal1)) { continue; } int diagonal2 = row + i; if (diagonals2.contains(diagonal2)) { continue; } queens[row] = i; columns.add(i); diagonals1.add(diagonal1); diagonals2.add(diagonal2); backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2); queens[row] = -1; columns.remove(i); diagonals1.remove(diagonal1); diagonals2.remove(diagonal2); } }}public ListgenerateBoard(int[] queens, int n) { List board = new ArrayList(); for (int i = 0; i < n; i++) { char[] row = new char[n]; Arrays.fill(row, '.'); row[queens[i]] = 'Q'; board.add(new String(row)); } return board;}????時間復雜度:O(n的n次方)
????空間復雜度:O(n+x)
非遞歸實現:
class Solution { public List> solveNQueens(int n) { List> lists = new ArrayList<>(); int i = 1; // 用數組a存儲棋子坐標,可以理解為i代表列,a[i]代表行 int[] a = new int[n+1]; while (i > 0) { // i為當前列,尋找前面各列與當前第i列的排斥情況,拿到的a[i]就是當前行i的合適a[i]列 for (a[i]++; a[i]<=n; a[i]++) if (check2(a, i)) break; // 如果a[i]列小于n,則可以繼續向后找 if (a[i] <= n) { // 如果當前行i就是第n行,則數量加1 if (i == n) { Listlist = new ArrayList<>(); for (int i2 : a) { StringBuilder sb = new StringBuilder(); for (int j = 0; j < n; j++) { if (j + 1 == i2) sb.append("Q"); else sb.append("."); } list.add(sb.toString()); } list.remove(0); lists.add(list); // 否則就是向后一列找,并且后面一列無論是有沒找過都要重置為0; } else { i++; a[i] = 0; } // 否則就是回溯,回到前一列(然后繼續向下面行找) } else { i--; } } return lists; } private static boolean check2(int[] a, int n) { for (int i=1; i if (Math.abs(a[i]-a[n])==Math.abs(i-n) || a[i]==a[n]) return false; } return true; }}????時間復雜度:O(n!)
????空間復雜度:O(n+x)
-----------------------------------未完-----------------------------------
????后面還有一個八皇后II,其實也就是大同小異,上面的是打印出棋盤,這個II就是計算個數(??這特么有啥區別?)
????所以直接貼代碼了。
遞歸實現:
public int totalNQueens(int n) { Set columns = new HashSet(); Set diagonals1 = new HashSet(); Set diagonals2 = new HashSet(); return backtrack(n, 0, columns, diagonals1, diagonals2);}public int backtrack(int n, int row, Set columns, Set diagonals1, Set diagonals2) { if (row == n) { return 1; } else { int count = 0; for (int i = 0; i < n; i++) { if (columns.contains(i)) { continue; } int diagonal1 = row - i; if (diagonals1.contains(diagonal1)) { continue; } int diagonal2 = row + i; if (diagonals2.contains(diagonal2)) { continue; } columns.add(i); diagonals1.add(diagonal1); diagonals2.add(diagonal2); count += backtrack(n, row + 1, columns, diagonals1, diagonals2); columns.remove(i); diagonals1.remove(diagonal1); diagonals2.remove(diagonal2); } return count; }}????時間復雜度:O(n的n次方)
????空間復雜度:O(n)
非遞歸實現:
public static int totalNQueens(int n) { int count = 0, i = 1; // 用數組a存儲棋子坐標,可以理解為i代表列,a[i]代表行 int[] a = new int[n+1]; while (i > 0) { // i為當前列,尋找前面各列與當前第i列的排斥情況,拿到的a[i]就是當前行i的合適a[i]列 for (a[i]++; a[i]<=n; a[i]++) if (check2(a, i)) break; // 如果a[i]列小于n,則可以繼續向后找 if (a[i] <= n) { // 如果當前行i就是第n行,則數量加1 if (i == n) { count++; // 否則就是向后一列找,并且后面一列無論是有沒找過都要重置為0; } else { i++; a[i] = 0; } // 否則就是回溯,回到前一列(然后繼續向下面行找) } else { i--; } } return count;}private static boolean check2(int[] a, int n) { for (int i=1; i if (Math.abs(a[i]-a[n])==Math.abs(i-n) || a[i]==a[n]) return false; } return true;}????時間復雜度:O(n!)
????空間復雜度:O(n)
????需要注意的是,遞歸的回溯法是一顆全部展開的樹,時間復雜度是N的N次方,很靈恐怖,雖然好理解,但是還是建議用迭代法。
--------------------------------------------完--------------------------------------------
當我望向你的時候,多希望你也在看著我。








轉換中輸出之插入/更新詳解)

)




)



