Kosaraju算法 有向圖的強連通分量

有向圖的強連通分量即，在有向圖G中，如果兩個頂點間至少存在一條路徑，稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通，稱G是一個強連通圖。非強連通圖有向圖的極大強連通子圖，稱為強連通分量(strongly connected components)。

采用的算法是Kosaraju算法。

算法原理：對于圖G，轉置圖（同圖中的每邊的方向相反）具有和原圖完全一樣的強連通分量。

具體實現：

1.對原圖G進行深度優先遍歷，記錄每個節點的離開時間time[i]。

2.選擇具有最晚離開時間的頂點，對反圖GT進行遍歷，刪除能夠遍歷到的頂點，這些頂點構成一個強連通分量。

3.如果還有頂點沒有刪除，繼續步驟2，否則算法結束。

貼一下看到的例圖：

原圖對圖進行DFS

對 逆圖進行DFS得強連通分量

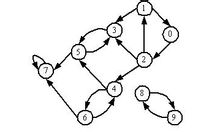
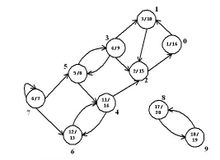
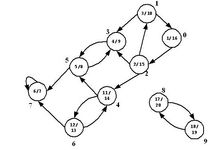
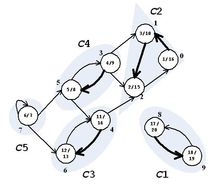
主要代碼：

intmap[511][511]; intnmap[511][511]; intvist[501]; stack<int>S; intN; intDFS1( intv ) /* vistthevnode */ { vist[v] = 1; for ( inti = 1; i <= N; i++ ) { if ( !vist[i] && nmap[v][i] ) DFS1( i ); } S.push( v ); return0; } intDFS2( intv ) { vist[v] = 1; for ( inti = 1; i <= N; i++ ) { if ( !vist[i] && map[v][i] ) DFS2( i ); } return0; } intkosaraju() { while ( !S.empty() ) S.pop(); memset( vist, 0, sizeof(vist) ); for ( inti = 1; i <= N; i++ ) { if ( !vist[i] ) { DFS1( i ); } } intt = 0; memset( vist, 0, sizeof(vist) ); while ( !S.empty() ) { intv = S.top(); S.pop(); printf( "|%d|", v ); if ( !vist[v] ) { t++; DFS2( v ); } } return t; </int>}