文末左下方閱讀原文指向了本人博客鏈接，不含廣告。參考資料中的相關鏈接，可以在博客文章的最下方獲取。推薦蘋果手機用戶使用淺色模式觀看。

前言

對于一些算法題，可以使用Python自帶的內置函數解決。但很多時候用就用了，根本不知道內部的細節。這樣的話，算時間復雜度和空間復雜度就很有問題。

因此，我最近幾天查閱了網上相關資料，并進行歸納和整理。開始我以為復制粘貼就行了，但是呢，我發現有很多東西都沒解釋得清楚與透徹，在研讀的過程中，我經常很懵逼，更有時候，我都懷疑自己智商了。

最后不得不逼自己讀相關源碼。越看源碼，越發現有很多可以分析的，但是考慮到篇幅和時間，就先打住，以后再整個進階版。

整理完這個以后，我認為呀，不管什么東西還是得追本溯源，這樣才靠譜。

目錄

• 前提說明

• 性能總結

• 1、列表(list)

  • 列表實現原理

  • 列表函數的時間復雜度

  • 列表函數講解

  • 性能分析

• 2、雙端隊列

  • 雙端隊列實現原理

  • 雙端隊列時間復雜度

  • 雙端隊列函數講解

  • 性能分析

• 3、字典(dict)

  • 字典實現原理

  • 字典函數的時間復雜度

  • 字典函數說明

  • 字典性能分析

• 4、集合(set)

  • 集合函數的時間復雜度

  • 集合性能分析

• 給自己留一個坑

• 參考資料

• 附錄

  • Cpython collections?部分源碼注釋

  • Cpython dict源碼部分注釋

前提說明

時間復雜度是參考官網:

https://wiki.python.org/moin/TimeComplexity

此頁面記錄了當前CPython中各種操作的時間復雜度(又名“Big O”或“大歐”)。其他Python實現(或CPython的舊版本或仍在開發版本)可能具有略微不同的性能特征。但是, 通常可以安全地假設它們的速度不超過O(log n)。

在所有即將介紹的表格中，n是容器中當前元素的數量，k是參數的值或參數中的元素數。

本文先上結論再進行分析，有助于帶著問題去思考答案。

性能總結

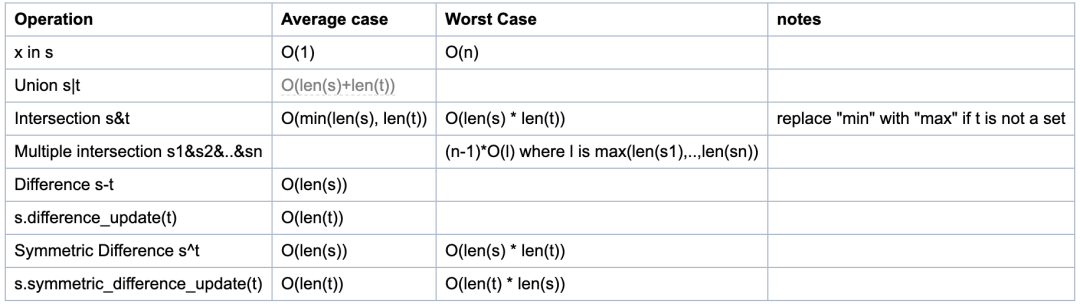
1、Python 字典中使用了 hash table，因此查找操作的復雜度為 O(1)，而 list 實際是個數組，在 list 中，查找需要遍歷整個 list，其復雜度為 O(n)，因此對成員的查找訪問等操作字典要比 list 更快。

2、set 的 union， intersection，difference 操作要比 list 的迭代要快。因此如果涉及到求 list 交集，并集或者差的問題可以轉換為 set 來操作。

3、需要頻繁在兩端插入或者刪除元素，可以選擇雙端隊列。

1、列表(list)

可直接使用，無須調用。

列表實現原理

列表是以數組(Array)實現的，這個數組是 over-allocate 數組。顧名思義，當底層數組容量滿了而需要擴充的時候，python依據規則會擴充多個位置出來。比如初始化列表array=[1, 2, 3, 4]，向其中添加元素23，此時array對應的底層數組，擴充后的容量不是5，而是8。這就是over-allocate的意義，即擴充容量的時候會多分配一些存儲空間。如圖1，展示了l.insert(1,5) 的操作。

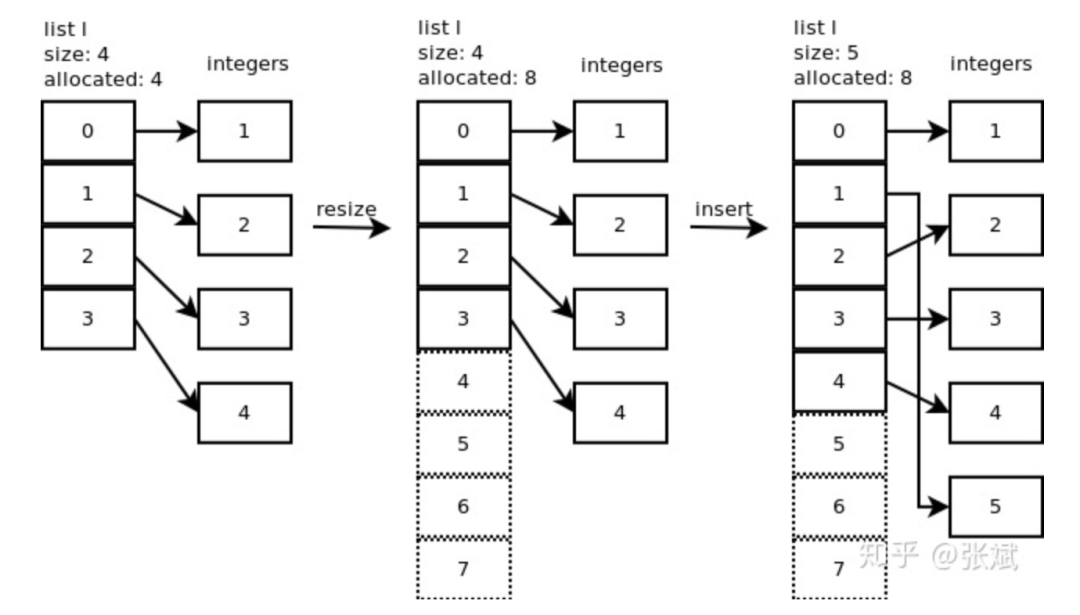
這里說下，列表的增長模式為：0，4，8，16，25，35，46，58，72，88...

列表函數的時間復雜度

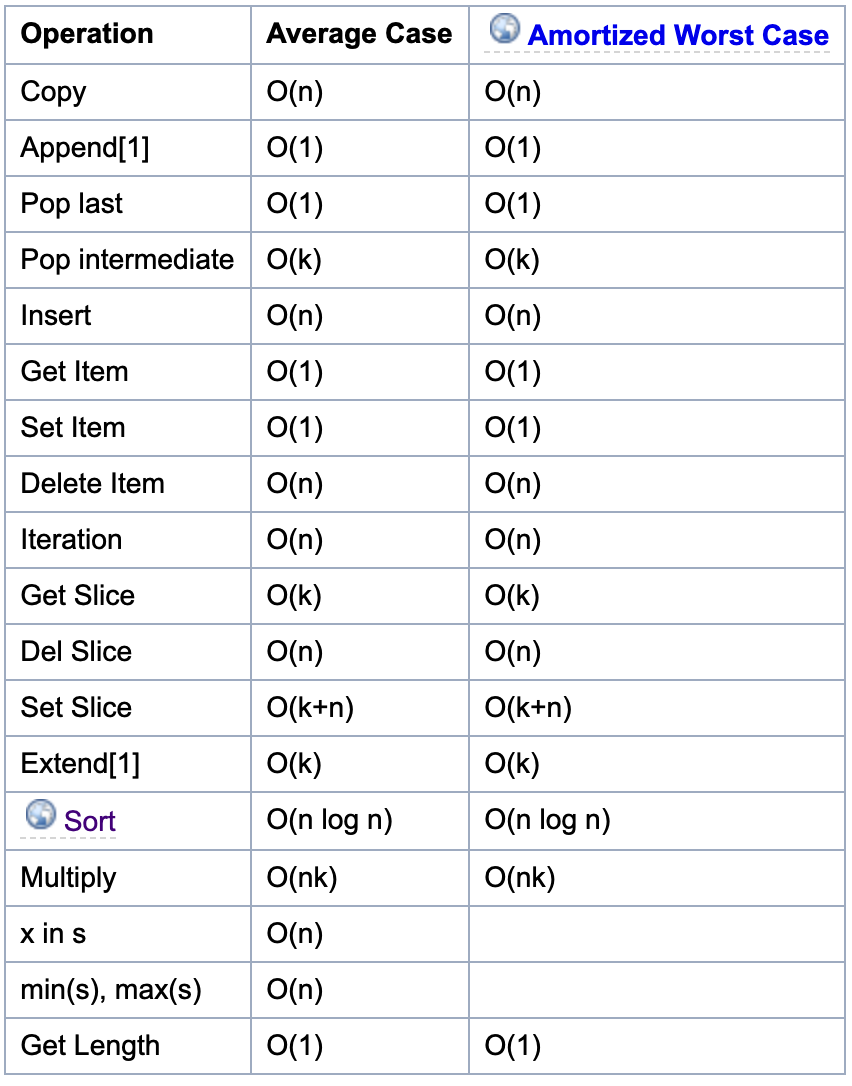
如果要更好地理解列表，就必須熟悉數組這種數據結構。如圖 2所示，為列表相關函數的時間復雜度。

列表函數講解

• append()方法是指在列表末尾增加一個數據項，這里的表強調的是插入1個元素，即沒有擴容。
• extend()方法是指在列表末尾增加一個數據集合；
• insert()方法是指在某個特定位置前面增加一個數據項，需要移動其他元素位置；
• len()方法獲取列表內元素的個數，因為在列表實現中，其內部維護了一個 Py_ssize_t 類型的變量表示列表內元素的個數，因此時間復雜度為O(1)；
• sort()方法是排序，網上有原理講解，使用的是 Timesort 排序，該排序結合了合并排序(merge sort)和插入排序(insertion sort)而得出的排序算法，它在現實中有很好的效率。空間復雜度為O(n)。其排序的過程大致為，對輸入的數字進行分區，然后再進行合并；

性能分析

通過對上表的分析可以發現，列表不太適合做元素的查找、刪除、插入等操作，因為這些都要遍歷列表，對應的時間復雜度為O(n)。

訪問某個索引的元素、尾部添加元素(append)或刪除(pop last)元素這些操作比較適合用列表做，對應的時間復雜度為O(1)。

根據官方上說，列表最大的開銷發生在超過了當前所分配的列表大小，這是因為，所有元素都需要移動；或者是在起始位置附近插入或者刪除元素，這種情況下所有在該位置后面的元素都需要移動。如果你需要在一個隊列的兩端進行增刪的操作，應當使用collections.deque。

如果我們要在業務開發中，判斷一個value是否在一個數據集中，如果數據集用列表存儲，那此時的判斷操作就很耗時，如果我們用hash table(set or dict)來存儲，則比較輕松。

2、雙端隊列

使用時，需要導入：

from collection import deque

雙端隊列實現原理

deque(雙端隊列)是以雙向鏈表的形式實現的。(好吧, 一個數組列表而不是對象, 以提高效率)。

為了更好地理解這種結構，可以參照 GitHub 上 CPython collections 模塊的第二個 commit 的源碼。注釋在文末的附錄下面。

這里根據注釋，我畫了一個不太準確的圖，其實leftblock和rightblock都是要存儲數據的。但在下圖，沒有標明。

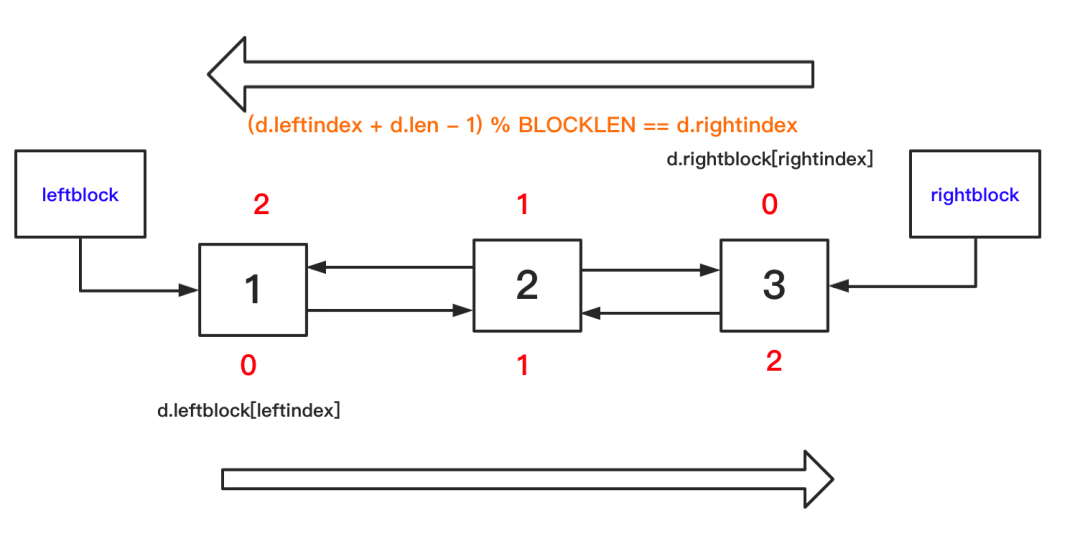
參考資料4，單個block的結構體示意圖如下：

總結來說，deque 內部將一組內存塊組織成雙向鏈表的形式，每個內存塊可以看成一個 Python 對象的數組， 這個數組與普通數據不同，它是從數組中部往頭尾兩邊填充數據，而平常所見數組大都是從頭往后。正因為這個特性，所以叫雙端隊列。

雙端隊列時間復雜度

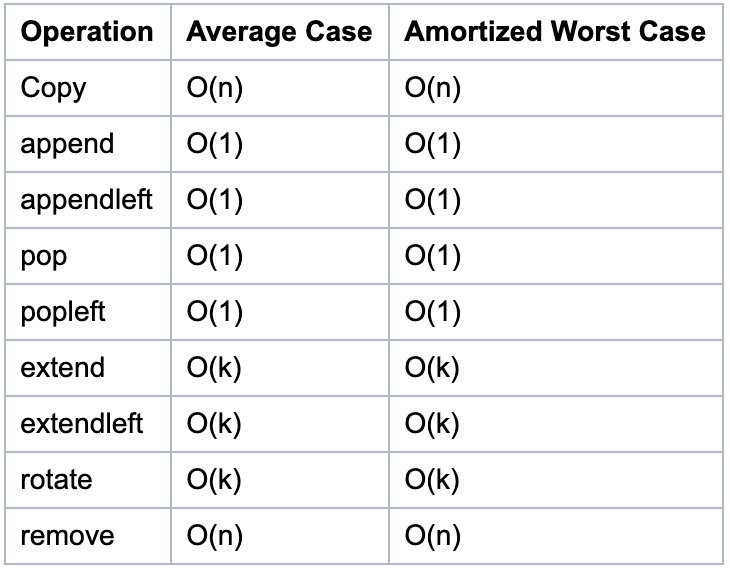
如圖所示，為雙端隊列的相關函數的時間復雜度。

雙端隊列函數講解

在這種數據結構下，append方法是怎么實現的呢？

1. 如果 rightblock 可以容納更多的元素，則放在 rightblock 中
2. 如果不能，就新建一個 block，然后更新若干指針，將元素放在更新后的 rightblock 中。

性能分析

得益于 deque 這樣的結構，它的 pop/popleft/append/appendleft 四種操作的時間復雜度均是 O(1), 用它來實現隊列、棧會非常方便和高效。

雖然雙端隊列中的元素可以從兩端彈出，并且隊列任意一端都可以入隊和出隊，但其限定插入和刪除操作在表的兩端進行。由于這樣，查找雙端隊列中間的元素較為緩慢, 增刪元素就更慢了。

3、字典(dict)

可直接使用，無須調用。

字典實現原理

在Python中，字典是通過哈希表實現的。也就是說，字典是一個數組，而數組的索引是經過哈希函數處理后得到的。要理解字典，必須對哈希表這種數據結構比較熟悉。下圖6為哈希表的一個邏輯判斷：

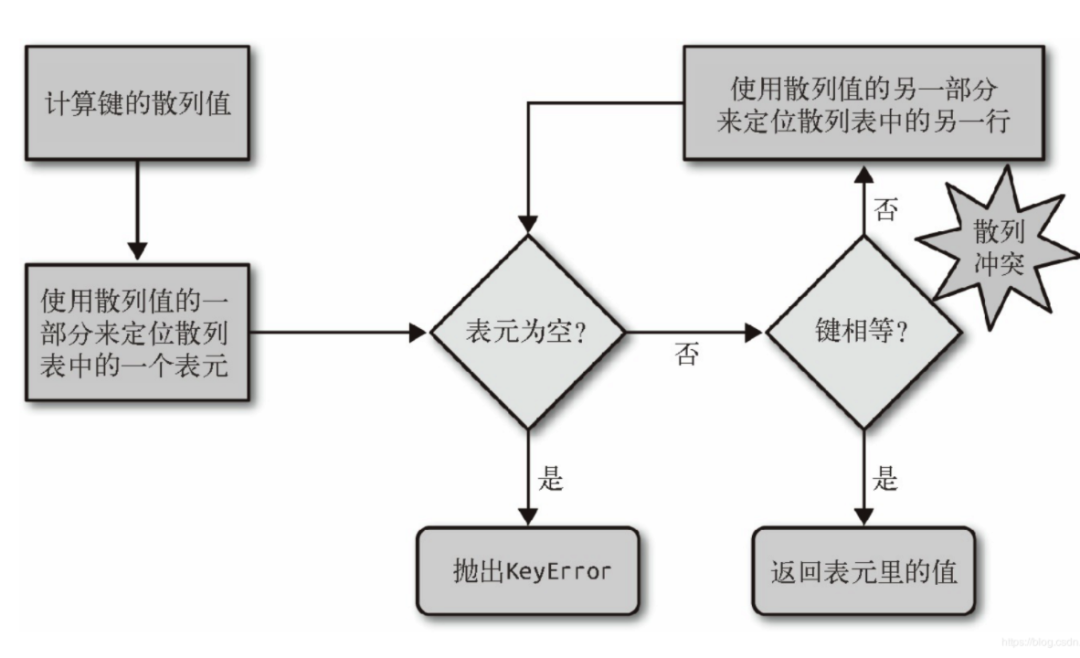
這里要注意幾點：

• 使用散列值的一部分進行定位
• 散列沖突時，使用散列值的另一部分，如果這一部分是包含原始Key的信息，那么不同的Key通過比較就能區分出來。

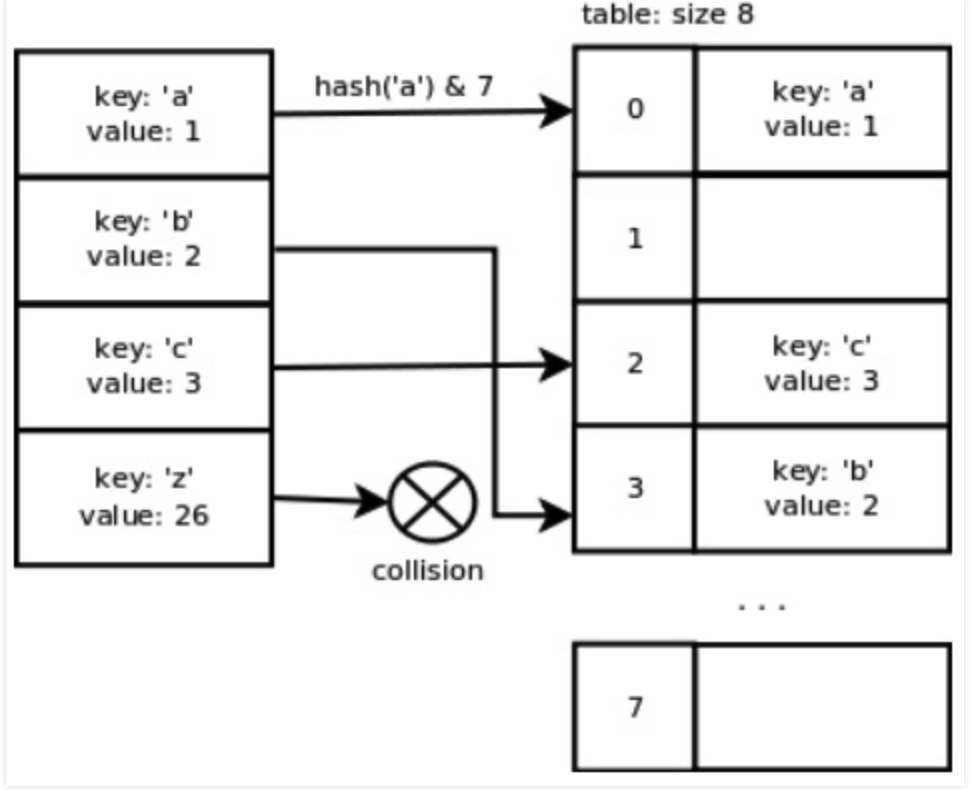
你可能會問，取哈希值的一部分是怎么取得呢？下圖7給了一個種方式，就是將計算得到哈希值 & 數組的長度。

同時，由這張圖，我們可以發現Python的哈希函數在鍵彼此連續的時候表現得很理想，這主要是考慮到通常情況下處理的都是這類形式的數據。然而，一旦我們添加了鍵'z'就會出現沖突，因為這個鍵值并不毗鄰其他鍵，且相距較遠。

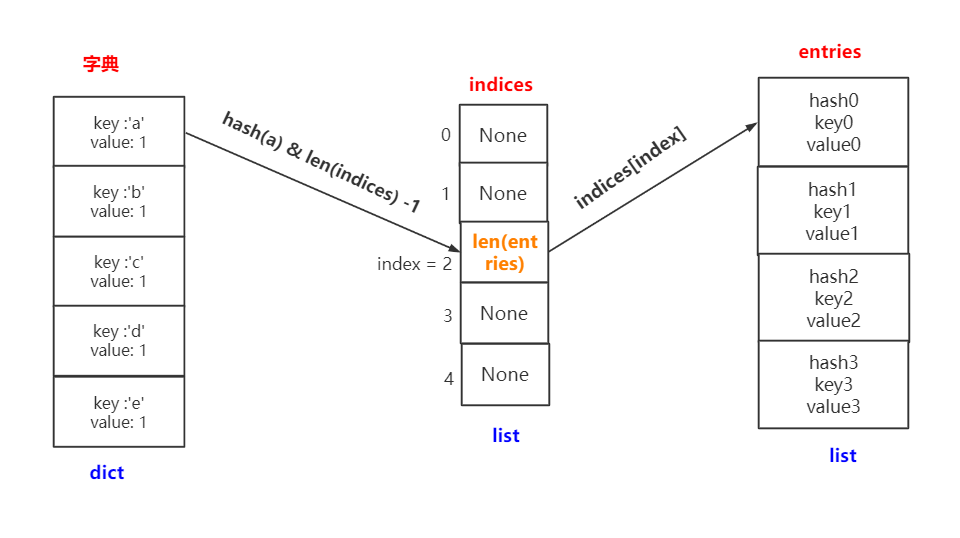
先要聲明的是，針對python的不同版本，dict的實現還有所不同，較為詳細的介紹請參考資料[6]。老字典只使用一張hash，而新字典還使用了一張Indices表來輔助。這里的indices才是真正的散列表哦，下來列出新的結構：

indices = [None, None, index, None, index, None, index]enteies = [ [hash0, key0, value0],  [hash1, key1, value1],  [hash2, key2, value2]]

字典存儲過程：

• 計算key的hash值 ( hash(key) )，再和mask做與操作 ( mask=字典最小長度(IndicesDictMinSize)- 1 )，運算后會得到一個數字index，這個index就是要插入的indices的下標位置(注：具體算法與Python版本相關，并不一定一樣)；
• 得到index后，會找到indices的位置，但是此位置不是存的hash值，而是存的len(enteies)，表示該值在enteies中的位置；
• 如果出現hash沖突，則會繼續向下尋找空位置(略有變化的開放尋址)，一直到找到剩余空位為止。

字典查找過程：

• 計算 hash(key)，得到hash_value ;
• 計算 hash_value & ( len(indices) - 1)，得到一個數字index ;
• 計算 indices[index] 的值，得到 entry_index ;
• 計算 enteies[entey_index] 的值 ，為最終值。

為方便理解，這里我做了一個圖，可以看到 indices 起到一個橋梁的作用。畫完這個圖，再感嘆一句，設計還是挺巧妙的。

這里補充下，關于哈希沖突，是怎么尋找下一個數組位置的。源碼中用到的是以下公式：

j = ((5*j) + 1) mod 2**i

這里的 j 有兩層含義，賦值號左邊的為數組的下一個下標，賦值號右邊的是當前發生沖突的下標。而 2 ** i可以理解數組長度。舉例說明，對于要給size大小為2 ** 3來說：

j_prev = 0 ; j_next = ((5 * 0) + 1) mod 8 = 1  j_prev = 1 ; j_next = ((5 * 1) + 1) mod 8  = 6j_prev = 6 ; j_next = ((5 * 6) + 1) mod 8  = 7j_prev = 7 ; j_next = ((5 * 7) + 1) mod  8 = 4j_prev = 4 ; j_next = ((5 * 4 ) + 1) mod 8 = 5

以此類推，最后回到起點為0。以下就是哈希沖突的軌跡

0 -> 1 -> 6 -> 7 -> 4 -> 5 -> 2 -> 3 -> 0

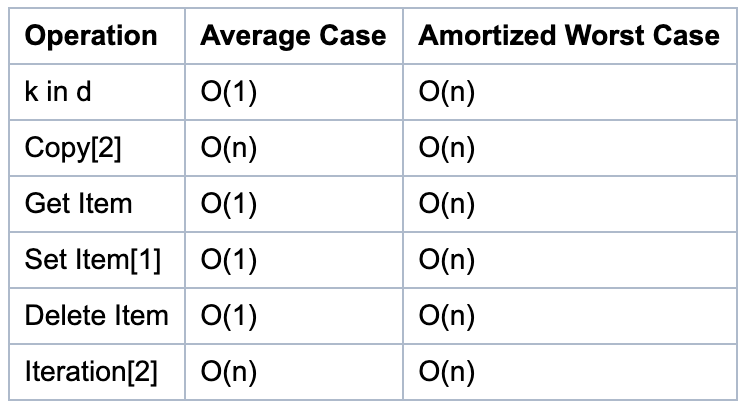
字典函數的時間復雜度

下列字典的平均情況基于以下假設：

1. 對象的散列函數足夠擼棒(robust), 不會發生沖突。
2. 字典的鍵是從所有可能的鍵的集合中隨機選擇的。

小竅門：只使用字符串作為字典的鍵。這么做雖然不會影響算法的時間復雜度, 但會對常數項產生顯著的影響, 這決定了你的一段程序能多快跑完。

字典函數說明

1. 這些操作依賴于“攤銷最壞情況”的“攤銷”部分。根據容器的歷史, 個別動作可能需要很長時間。
2. 對于這些操作, 最壞的情況n是容器達到的最大尺寸, 而不僅僅是當前的大小。例如, 如果一個N個元素的字典, 然后刪除N-1個元素, 這個字典會重新為N個元素調整大小, 而不是當前的一個元素, 所以時間復雜度是O(n)。

字典性能分析

字典的查詢、添加、刪除的平均時間復雜度都是O(1)，相比列表與元祖，性能更優。但是，如果發生散列沖突，或者容器需要擴充，那么時間復雜度就要考慮最差的情況 O(n)。所以說字典及其依賴哈希算法，真正要靈活運用詞典時，還需要查看底層的哈希算法。

4、集合(set)

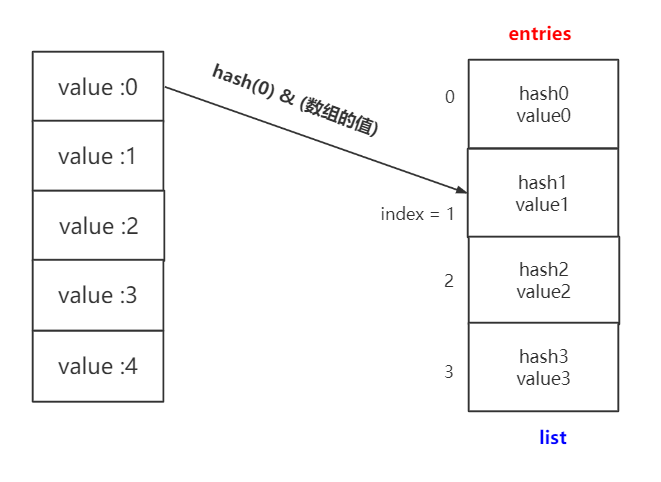
dict與set實現原理是一樣的，都是將實際的值放到list中。唯一不同的在于hash函數操作的對象，對于dict，hash函數操作的是其key，而對于set是直接操作的它的元素。

假設操作內容為x，其作為因變量，放入hash函數，通過運算后取list的余數，轉化為一個list的下標，此下標位置對于set而言用來放其本身。

而對于dict則是創建了兩個list，一個listf存儲哈希表對應的下標，另一個list中存儲哈希表具體對應的值。

這里為了更好地理解，對比上面字典那個圖，我嘗試畫一個圖。

集合函數的時間復雜度

下圖是函數的時間復雜度：

集合性能分析

由源碼得知, 求差集(s-t, 或s.difference(t))運算與更新為差集(s.difference_uptate(t))運算的時間復雜度并不相同！

• 第一個是O(len(s))(對于s中的每個元素, 如果不在t中, 將它添加到新集合中)。
• 第二個是O(len(t))(對于t中的每個元素, 將其從s中刪除)。

因此, 必須注意哪個是首選, 取決于哪一個是最長的集合以及是否需要新的集合。

集合的s-t運算中, s和t都要是set類型。如果t不是set類型, 但是是可迭代的, 你可以使用等價的方法達到目的, 比如 s.difference(l), l是個list類型。

另外，列表的一些集合運算，可以轉成集合類型來操作，速度更快。

給自己留一個坑

自己也嘗試讀了一下一些數據結構的源碼，雖然很多看不懂，但是抓到一些關鍵信息。比如下面的代碼和圖片。

static Py_ssize_tlist_length(PyListObject *a){return Py_SIZE(a);}

下圖為dictobject.c里的一個函數：

參考資料

[1] ?Python內置方法的時間復雜度

[2] TimeComplexity

[3] python list 之時間復雜度分析

[4] How collections.deque works?，

[5] 深入 Python 列表的內部實現；

[6] Python字典dict實現原理

附錄

Cpython?list?部分源碼注釋

源碼地址傳送門：https://github.com/python/cpython/blob/master/Objects/listobject.c

/* This over-allocates proportional to the list size, making room* for additional growth. The over-allocation is mild, but is* enough to give linear-time amortized behavior over a long* sequence of appends() in the presence of a poorly-performing* system realloc().* Add padding to make the allocated size multiple of 4.* The growth pattern is: 0, 4, 8, 16, 24, 32, 40, 52, 64, 76, ...* Note: new_allocated won't overflow because the largest possible value* is PY_SSIZE_T_MAX * (9 / 8) + 6 which always fits in a size_t.*/

Cpython collections?部分源碼注釋

源碼地址傳送門：https://github.com/python/cpython/blob/master/Modules/_collectionsmodule.c

/* The block length may be set to any number over 1.? Larger numbers* reduce the number of calls to the memory allocator but take more* memory.? Ideally, BLOCKLEN should be set with an eye to the* length of a cache line.*/#define BLOCKLEN 62#define CENTER ((BLOCKLEN - 1) / 2)/* A `dequeobject` is composed of a doubly-linked list of `block` nodes.* This list is not circular (the leftmost block has leftlink==NULL,* and the rightmost block has rightlink==NULL).? A deque d's first* element is at d.leftblock[leftindex] and its last element is at* d.rightblock[rightindex]; note that, unlike as for Python slice* indices, these indices are inclusive on both ends.? By being inclusive* on both ends, algorithms for left and right operations become* symmetrical which simplifies the design.* The list of blocks is never empty, so d.leftblock and d.rightblock* are never equal to NULL.* The indices, d.leftindex and d.rightindex are always in the range*???? 0 <= index < BLOCKLEN.* Their exact relationship is:*???? (d.leftindex + d.len - 1) % BLOCKLEN == d.rightindex.* Empty deques have d.len == 0; d.leftblock==d.rightblock;* d.leftindex == CENTER+1; and d.rightindex == CENTER.* Checking for d.len == 0 is the intended way to see whether d is empty.* Whenever d.leftblock == d.rightblock,*???? d.leftindex + d.len - 1 == d.rightindex.* However, when d.leftblock != d.rightblock, d.leftindex and d.rightindex* become indices into distinct blocks and either may be larger than the* other.*/

Cpython dict源碼部分注釋

源碼地址傳送門：https://github.com/python/cpython/blob/master/Objects/dictobject.c

/*layout:+---------------+| dk_refcnt?????????|| dk_size????????????|| dk_lookup???????|| dk_usable????????|| dk_nentries??????|+---------------+| dk_indices???????||?????????????????????????|+---------------+| dk_entries???????||?????????????????????|+---------------+dk_indices is actual hashtable. It holds index in entries, or DKIX_EMPTY(-1)?orDKIX_DUMMY(-2).dk_entries is array of PyDictKeyEntry. Its size is USABLE_FRACTION(dk_size).DK_ENTRIES(dk) can be used to get pointer to entries.The first half of collision resolution is to visit table indices via thisrecurrence:But catering to unusual cases should not slow the usual ones, so we just take?the last i bits anyway. It's up to collision resolution to do the rest. Ifwe *usually* find the key we're looking for on the first try (and, it turns?out, we usually do -- the table load factor is kept under 2/3, so the oddsare solidly in our favor), then it makes best sense to keep the initial index?computation dirt cheap.j = ((5*j) + 1) mod 2**iFor any initial j in range(2**i), repeating that 2**i times generates eachint in range(2**i) exactly once (see any text on random-number generation forproof). By itself, this doesn't help much: like linear probing (settingj += 1, or j -= 1, on each loop trip), it scans the table entries in a fixedorder. This would be bad, except that's not the only thing we do, and it'sactually *good* in the common cases where hash keys are consecutive.In an example that's really too small to make this entirely clear, for a table ofsize 2**3 the order of indices is:0 -> 1 -> 6 -> 7 -> 4 -> 5 -> 2 -> 3 -> 0 [and here it's repeating]*/