**************************************
注:本系列博客是博主學習Stanford大學 Andrew Ng 教授的《機器學習》課程筆記。博主深感學過課程后,不進行總結非常easy遺忘,依據課程加上自己對不明確問題的補充遂有此系列博客。本系列博客包含線性回歸、邏輯回歸、神經網絡、機器學習的應用和系統設計、支持向量機、聚類、將維、異常檢測、推薦系統及大規模機器學習等內容。
**************************************
多變量線性回歸
多維特征
眼下為止,我們探討了單變量(特征)的回歸模型,如今我們對房價模型添加很多其它的特征,如房間數樓層等,構成一個含有多個變量的模型,模型中的特征為(x ,x ,...,x )。
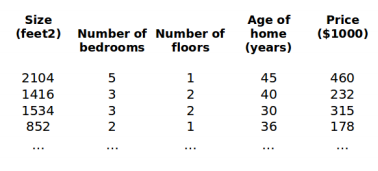
多變量梯度下降
與單變量線性回歸類似,在多變量線性回歸中,我們也構建一個代價函數,則這個代價函數是全部建模誤差的平方和。即:
當中:
我們的目標和單變量線性回歸問題中一樣,是要找出使得代價函數最小的一系列參數。 ?多變量線性回歸的批量梯度下降算法為:?
左邊為單變量學習方法,右邊為多變量學習方法。
梯度下降法實踐
1 特征縮放
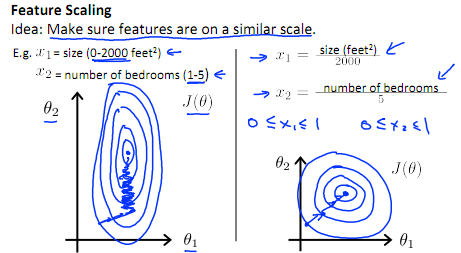
在我們面對多維特征問題的時候,我們要保證這些特征都具有相近的尺度。這將幫助梯度下降算法更快地收斂。
以房價問題為例,如果我們使用兩個特征,房屋的尺寸和房間的數量,尺寸的值為 0-2000平方英尺,而房間數量的值則是0-5,以兩個參數分別為橫縱坐標,繪制代價函數的等高線圖能,看出圖像會顯得非常扁,梯度下降算法須要非常多次的迭代才干收斂。
解決辦法是嘗試將全部特征的尺度都盡量縮放到-1 到1之間。如圖:
最簡單的方法是令:
2 學習率
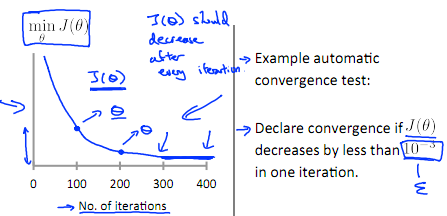
梯度下降算法收斂所須要的迭代次數依據模型的不同而不同,我們不能提前預知。我們能夠繪制迭代次數和代價函數的圖表來觀測算法在何時趨于收斂。
梯度下降算法的每次迭代受到學習率的影響,假設學習率 α過小,則達到收斂所需的迭代次數會很高。假設學習率α 過大,每次迭代可能不會減小代價函數。可能會越過局部最小值導致無法收斂。
通常能夠考慮嘗試些學習率:α=0.01,0.03,0.1,0.3,1,3,10?
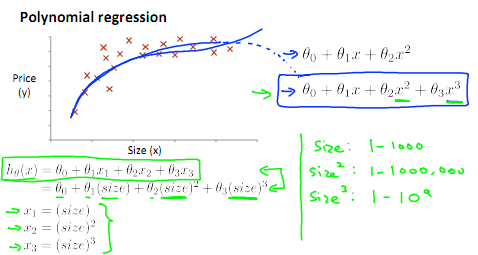
特征和多項式回歸
如房價預測問題:
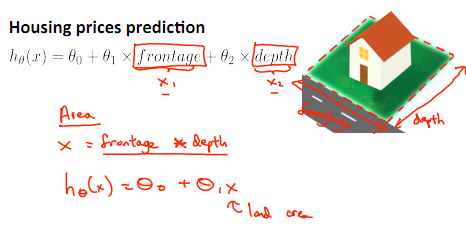
線性回歸并不適用于全部數據,有時我們須要曲線來適應我們的數據,通常我們須要先觀察數據然后再決定準備嘗試如何的模型。
另外,我們能夠將模型轉化為線性回歸模型。
例如以下圖 x->size:
注:假設我們採用多項式回歸模型,在執行梯度下降算法前,特征縮放很有必要。?
正規方程
到眼下為止。我們都在使用梯度下降算法,可是對于某些線性回歸問題,正規方程方法是更好的解決方式,它能夠直接解出參數。如:
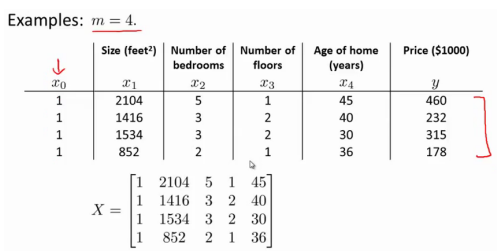
如果我們的訓練集特征矩陣為X(包括了 x0=1)而且我們的訓練集結果為向量 y。則利用正規方程解出向量:
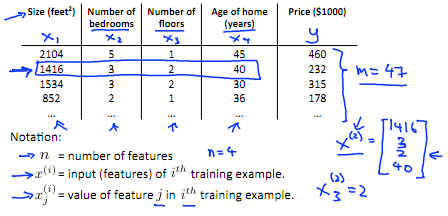
下面表示數據為例:
?
則依據公式: ?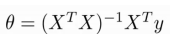
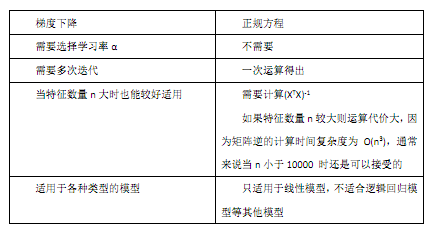
梯度下降與正規方程的比較:?
******************
作者:hao_09
時間:2015/8/9
文章地址:http://blog.csdn.net/lsh_2013/article/details/47374045
******************
??

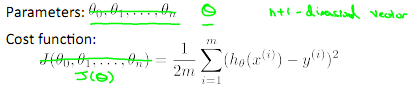

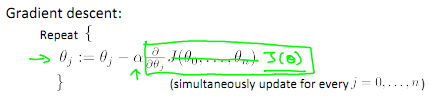

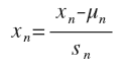

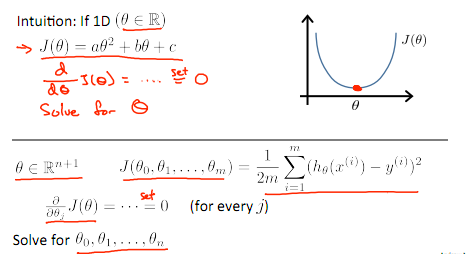

)






)

作用)


)





