? ? ? ? ? ? ? ?在橫斷面研究中，Log-binomial 模型能夠獲得研究因素與結局變量的關聯強度指標患病率比（PR），是一種研究二分類觀察結果與多因素之間關系的重要方法，在醫學研究等領域中得到了廣泛的應用。

采用log-binomial 模型可直接估計PR, ?log-binomial模型的因變量y服從二項分布 ，且因變量(y= 1)概率的對數與自變量呈線性關系：

?

其中，

?

β表示控制其他自變量時 ， 自變量X 與Y之間的回歸系數 ，PR = exp ( β)

01適用情形
?

但當事件的發生率較高(>10%)時 ，若仍用OR描述關聯強度，則會高估暴露與結局的關聯。因此，很多學者建議采用現患比（PR）描述暴露與結局的關聯強度。

?

當存在連續型自變量時，可能導致log-binomial 模型出現不收斂的情況，這是則可采用COPY方法（數據集擴充，后面會介紹）。

02案例分析

假設有因變量Y與自變量X1，X2, X3, X4 等；因變量Y（二分類）患病率大于20%，自變量X1 為年齡age（連續型變量），其他均為分類變量；

對于此案例，最直接的方法是采用logistic回歸模型，但是Y患病率大于20%，可能會高估OR值。因此，本例使用Log-binomial 模型的PR值來估計患病率與研究因素的關聯強度

03 SAS?程序實例
?

PROC GENMOD 的詳細使用可參照SAS help 手冊。

?

?

在SAS/STAT中，通過PROC GENMOD 程序實現

數據集名為Log_binomial，參數統計量輸出到Log_binomial _y中；

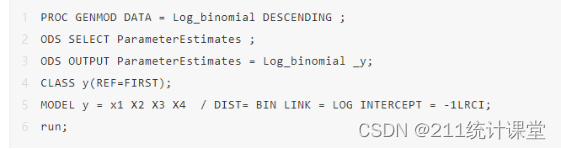
定義數據集OUT-para,? 計算PR, LPR, UPR; 并打印

?

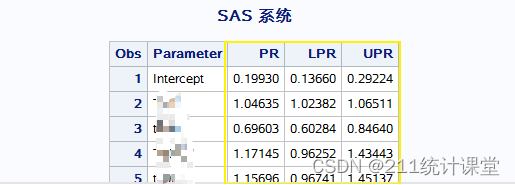
輸出結果

?

?

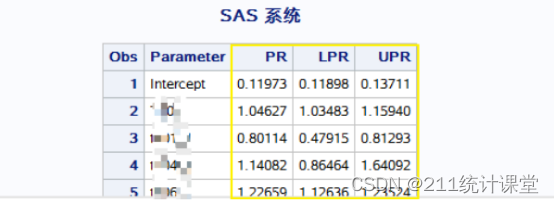
但是，日志中警告 模型出現不收斂。可能的原因與很多，其中連續型自變量age可能導致模型出現不收斂；
下面采用COPY方法對數據集進行擴張。

04 SAS程序示例—COPY方法
?

當存在連續型自變量時， MLE（maximum likelihood estimation）估計的參數通常在參數所限制范圍的邊界上 ，MLE得不到似然函數導數為零的極大值點，導致模型不能收斂。

Deddens等學者提出先對原始數據集調整擴充后再擬合 log-binomial模型，稱為COPY方法擴充原始數據集的步驟：當log-binomial 回歸模型不收斂時，將原始數據集中Y=1的個案增加 c-l倍 ，然后再將原始數據集Y值互換 ，將這兩個新的數據集合并成一個數據集， 即為復制(COPY )數據集 ，?再利用 COPY 數據集擬合log-binomial 回歸模型從而達到解決模型不收斂問題 。

通常C為常數 ，C越大(通常取1000) ，COPY數據集的偽似然估計值越接近于最大似然估計值 。在 SAS 軟件中， 可以利用 genmod 模塊中的加權log-binomial回歸模型實現COPY 數據集下的log-binomial回歸方法 。

---

對數據集log-binomial 進行復制，其中，c=1000;

?

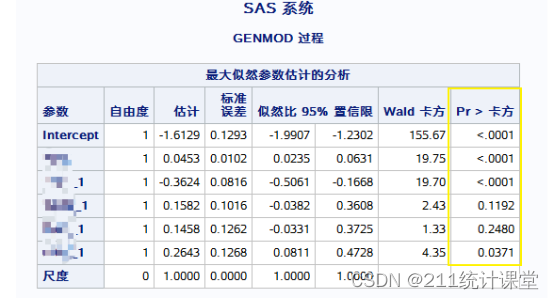
再對數據進行log-binomial模型分析,應特別注意需要對?w 進行加權處理

?

結果輸出

?

?

05 logistic回歸模型與log-binomial模型的對比
?

從調整OR值和PR值可看出，log-binomial模型計算出的PR值要更接近與1。

?