? ? ? ? 本文針對過去兩周的深度學習理論做階段性回顧，學習資料來自吳恩達老師的2021版deeplearning.ai課程，內容涵蓋深度神經網絡改善一直到ML策略的章節。視頻鏈接如下：吳恩達深度學習視頻鏈接

? ? ?（注：本文出自深度學習初學者，此文內容將以初學者的感悟與見解講述。當然我也會努力搜尋資料以彌補自身認知的不足，希望本文能對深度學習的其他初學者也有所幫助，文章若有不當之處，望大家在評論區多多指正，我將虛心接納，多謝！）

Charpter1: 改善神經網絡

1.訓練集，開發集，測試集

? ? ? ? 深度學習的關鍵組成部分是神經網絡，而神經網絡具有深層次的網絡結構，是一種依靠大量數據樣本，通過正向傳播、逆向傳播算法對數據進行訓練與學習，進而提取復雜數據特征與模式，從而完成指定任務的計算模型。正如小孩子通過體察世界、閱讀書籍等方式認知世界，機器的學習也需要借助學習原料，這些原料就是大量的樣本數據。（注：已有了解的同學可跳過段）

? ? ? ? 模型構建的過程常包括模型的訓練，模型參數的調整以及模型的精確度檢驗，對應的所需數據集合成為訓練集，開發集與測試集。

? ? ? ? 1.1三個數據集的基本概念

? ? ? ? 訓練集指構建深度學習模型的數據集，機器需要依靠大量數據來識別與認知這個世界，而訓練集就是機器的學習材料，使機器學習與認識輸入數據與對應數據的標簽輸出之間的關系，讓模型不斷通過優化迭代算法，調節模型的參數與權重，最大限度地減少模型在訓練集上地訓練誤差。

? ? ? ? 開發集用于調節與選擇模型的超參數與結構，機器在開發集上進行模型選擇、調整和驗證，評估模型的性能、進行參數調優，并避免對訓練集的過擬合，對于模型構建起到關鍵的評估與選擇的作用，從而提高模型在測試集上的泛化能力。

? ? ? ? 測試集用于最終評估模型的性能與泛化能力，衡量模型在真實環境下的效果與實際的預測能力。

? ? ? ? 三個數據集往往相互獨立，如果機器也能參加高考，那么三個數據集的作用比喻為：訓練集是機器學習的學習原材料，用于學習知識點與掌握考點；然而單憑學習還不足以證明你有所掌握，此時開發集就是檢驗你學習效果的模擬考試，機器在模擬考試之后也會查漏補缺（對應為模式選擇與參數調優等操作），從而擴充與鞏固知識點；測試集便是機器的高考，用于檢驗“高中三年”學習訓練的最終效果。若成績優良，那自然是皆大歡喜，否則只能含淚復讀了（重新訓練或則調節參數）。

1.2 偏差與方差

? ? ? ? 偏差與方差是機器學習中的兩個重要概念，用于衡量機器在訓練樣本與新樣本上的預測效果，與欠擬合與過擬合之間存在著密切的關系。

? ? ? ? 偏差是指模型對于訓練樣本的預測值與真實值之間的差距，比如貓識別器識別一張貓圖為非貓圖，則稱預測結果與真實值不符，存在偏差。高偏差通常意味著模型未能提取數據中的特征與模式，無法對數據的真實分布進行準確建模，導致欠擬合問題。

? ? ? ? 方差是指模型預測結果的變化程度，它反映了模型對訓練數據的敏感性和抗干擾能力，方差較高的模型對訓練集的小波動過度敏感，可能過度擬合訓練數據中的噪聲。低偏差與高方差的模型可能表現出良好1的擬合能力，當新數據上的泛化能力較差，導致過擬合。

2.欠擬合與過擬合

? ? ? ? 2.1判別擬合的方法

? ? ? ? 判別模型的擬合類別比較簡單，欠擬合的判斷方法是看模型在訓練集上的預測值與真實值上的差距，如果差距較大，出現了高偏差，那么說明模型出現了欠擬合問題，模型還沒能提取出數據的復雜特征模式。

? ? ? ? 判斷過度擬合的方式是，在模型出現低偏差的條件下，看模型是否在新的數據集上出現高方差，即模型雖然能夠很好地擬合訓練集上的數據，但對于新數據缺乏擬合能力，謂之模型出現了過擬合問題。可見，新數據可來源于開發集與測試集。

? ? ? ? 2.2 欠擬合與過擬合的圖解

欠（過）擬合

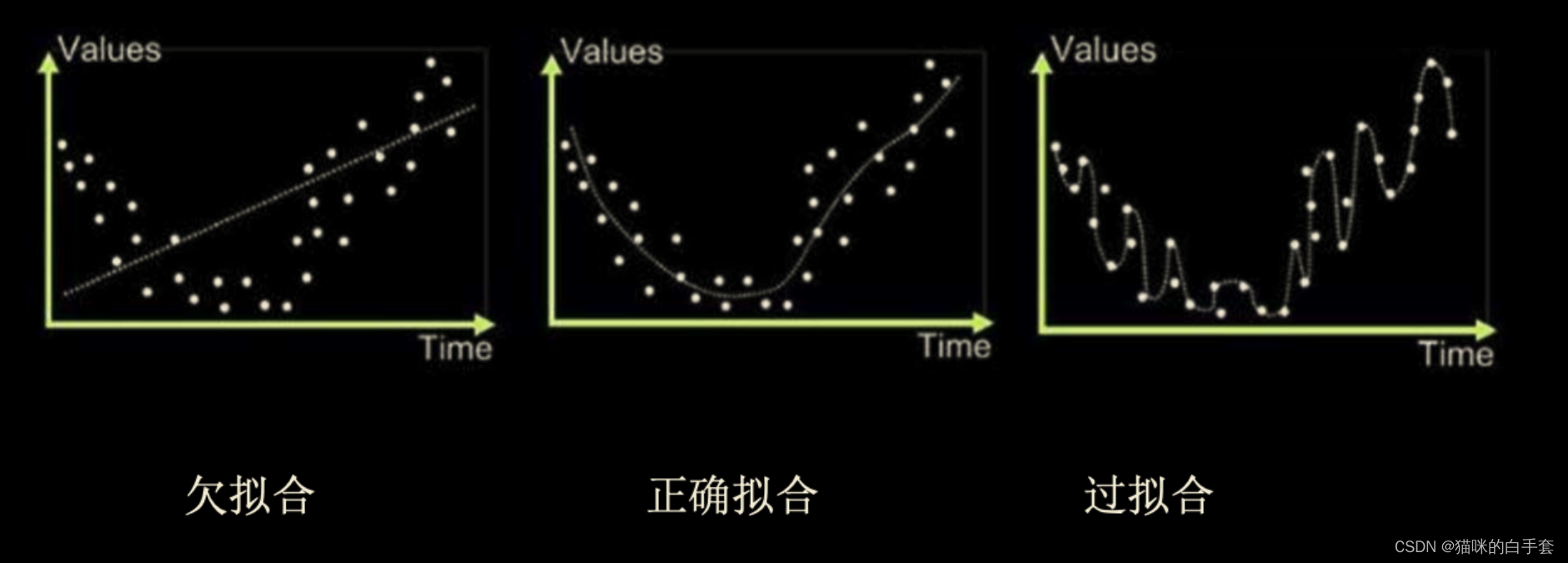
? ? ? ? （注：圖片來源于博客http://t.csdn.cn/lNUAn）?

? ? ? ? 上圖展示構建曲線擬合數據樣本點的特征，曲線一出現欠擬合問題，模型無法擬合訓練樣本的數據特征，預測值與真實值存在高偏差（高誤差），即模型出現欠擬合；曲線二則是恰當的擬合曲線，即模型能夠提取數據的模式并擬合出數據樣本的總體特征；曲線三出現了過擬合問題，模型學習訓練集時學得過于精細了（曲線經過了訓練數據的所有點），過度適應了訓練數據集合，導致模型在新的數據上缺乏預測能力。

? ? ? ? 2.3解決方法

? ? ? ? 解決欠擬合的方法有：增加模型復雜度、引入更多特征、增加訓練數據量等；

? ? ? ? 解決過擬合的方法有：降低模型復雜度、增加正則化技術、增加訓練數據等，以下將著重講解正則化技術。

3.正則化技術

? ? ? ? 正則化技術的用途在于解決模型的過擬合問題，而模型的過擬合問題常常來源于訓練數據不足、模型網絡過于復雜（學習能力太強了）、模型參數過多且權重過大、數據特征選擇不當、數據標注錯誤、訓練時間過長等原因，以下將講解正則化技術是如何解決過擬合問題。

? ? ? ? （注：本人對于正則化技術的理解來源于這位大佬的博客http://t.csdn.cn/TfZF0，所謂站在巨人的肩膀上才能學得更快，感興趣的同學可以通過該博客了解正則化技術，本博客畢竟也只是初學者的見解！）

? ?3.1 L1正則化

? ? ? ? 3.1.1 公式解釋

? ? ? ? $L1$ 正則化通過在損失函數中添加模型參數絕對值之和的懲罰項，將大部分參數壓縮為0，從而實現特征選擇和稀疏性。它傾向于生成稀疏權重向量，可以用于特征選擇，即通過減小不相關的特征的權重使其趨近于0.

? ? ? ?? $L1$ 正則化的損失函數： $Loss_{regulation} = Loss_{origin} + \frac{\lambda}{n}\sum_{i=1}^{n}|w_{i}|$

? ? ? ?? $L1$ 正則化的參數偏導： $dw_{regulation} = dw_{origin}+\frac{\lambda}{n}$

? ? ? ? 新的損失函數在原損失函數的基礎上添加了參數絕對值之和的懲罰項，其中 $\lambda$ 是懲罰系數， $\lambda$ 越大,懲罰就越狠。由于模型在梯度下降算法下，以損失函數最小化為目標，而新添的參數絕對值之和會增大損失函數，這意味著模型在訓練的過程中，傾向于把參數變小。而參數代表模型對于數據某個特征賦予的權重，當損失函數渴望變小的同時保留對于訓練數據的擬合能力，那么它就只能保留那些最重要且最能概括訓練數據特征的參數權重，其余代表復雜特征的參數權重統統置為0（或很小值），從而提高了模型的泛化能力，解決了過擬合問題。

? ? ? ? 3.1.2舉個栗子

? ? ? ? 舉個例子（當然大佬那篇博客的例子也很不錯，本人的例子不愿看可直接跳過），假設我們需要訓練一個貓識別器，且為了簡化問題只考慮貓的毛色與形態兩個特征。我們知道凡是貓都具有普遍的形態：體型小，全身毛被密而柔軟，鎖骨小，吻部短，眼睛圓，頸部粗壯，四肢較短，足下有數個球形肉墊，舌面被有角質層的絲狀鉤形乳突等等；但貓的毛色卻不盡相同，有白，黃，棕等等，屈指難數，如下為一些不同毛色貓貓的圖片：

???????

? ? ? ? ?當我們的訓練樣本較少（假設只有上面四張圖片）且網絡結構較復雜（識別復雜特征的能力較強）時，模型同時記住貓的形態與這些貓的各種膚色，此時便出現了過擬合。它會認為只有當新測試樣本（假設也是一貓但它的膚色不屬于上述任意一種）滿足貓的形態且貓的膚色滿足上述四種顏色時，這個測試樣本才會被判斷為貓。由于新樣本的膚色特征不符合模型要求，所以它被錯判為非貓了。

? ? ? ? 為了解決這種過擬合問題，我加入懲罰項，迫使模型忘記數據的復雜特征，而只記住普遍特征，于是機器就思考：由于貓的膚色各不相同，若學習這些膚色特征需要消耗大量成本（給每個復雜特征對應的參數賦予高權重，導致損失函數數值過大），但如果只單獨學習貓的形態其實便能判斷一個動物是否貓，因此它單獨學習貓的形態這一貓的普遍特征，因而當新的貓圖輸入時便能很自然被機器判斷為貓啦！

? ? ? ? 3.1.3 L1正則化求解稀疏解

? ? ? ? 關于L1正則化是如何產生稀疏解的疑問，我覺得大佬的那篇博客已經解釋得夠清楚，而本人由于數學能力有限在此也難做解釋，但也可以給出一些我的思考：由于模型訓練的本質就是調節參數，而損失函數是關于參數的函數，訓練目的在于找到損失函數的最優解。當我們限定參數的絕對值之和為一個定值時，由于訓練參數較多，高維參數的絕對值之和為定值在高維空間中的圖像是某個高維的幾何體，幾何體的端點比較突出，往往容易觸碰到損失函數的最優解領域，從而對于參數向量 $v = \{w_{1},w_2.\cdots,w_n\}$ 只有少部分分量大于0，而大部分分量等于0，因而得到稀疏解。（注：本人也自覺解釋得不到位，恰當的解釋還是建議看大佬的博客，或者也可以參考這篇博客：http://t.csdn.cn/9bjhl）

3.2 L2正則化

???????? $L2$ 正則化通過在損失函數中添加模型參數平方和的懲罰項，限制模型參數的值域大小。 $L2$ 正則化會使模型的參數接近于0，但不等于0，因此不會得到稀疏權重向量。它對異常值的敏感度較低，可以有效地防止過擬合。

? ? ? ? 3.2.1 公式解釋

???????? $L2$ 正則化損失函數： $Loss_{regulation} = Loss_{origin}+\frac{\lambda}{2n}\sum_{i=1}^{n}w_{i}^2$

? ? ? ?? $L2$ 正則化參數偏導： $dw_{regulation} = dw_{origin}+\frac{\lambda}{n}w$

? ? ? ? 關于 $L2$ 正則化如何通過懲罰項解決正則化問題，其道理與 $L1$ 正則化解決過擬合問題的道理是互通的，在此不多加解釋。

? ? ? ? 3.2.2 $L1$ 與 $L2$ 正則化的區別

計算方式的不同：兩者在損失函數與參數偏導上的所添加的公式不同；
參數限制程度： $L1$ 正則化鼓勵模型的參數稀疏性，即通過將一部分參數的權重推向零來減少特征的依賴性； $L2$ 正則化更傾向于將參數權重均勻地減小，但不會強制將其推向零。L2正則化會使得模型的參數權重趨向于較小的值，但不會稀疏參數；
形狀： $L1$ 正則化項形狀是由參數的絕對值之和構成的一個等邊矩形（L1范數的等值線為菱形），其對應的正則化項的圖像為“角”狀； $L2$ 正則化的正則化項形狀是由參數的平方和的平方根構成的一個球體（L2范數的等值線為圓），其對應的正則化項的圖像為“球”狀；

3.3 Dropout正則化?

? ? ? ? Dropout是一種特殊的正則化技術，其基本思想是在訓練過程中以一定的概率丟棄（置零）隨機選擇的隱藏層單元。這樣可以防止某些特征值過度依賴于特定的隱藏單元，并促使模型學習到多個獨立的特征表示。通過隨機丟棄隱藏層單元，正則化抑制可以減少模型對特定訓練樣例的過度依賴，從而提高泛化能力和魯棒性.

? ? ? ? 3.3.1 python代碼實現

? ? ? ? Dropout的正向傳播代碼:

# GRADED FUNCTION: forward_propagation_with_dropoutdef forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):"""Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.Arguments:X -- input dataset, of shape (2, number of examples)parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":W1 -- weight matrix of shape (20, 2)b1 -- bias vector of shape (20, 1)W2 -- weight matrix of shape (3, 20)b2 -- bias vector of shape (3, 1)W3 -- weight matrix of shape (1, 3)b3 -- bias vector of shape (1, 1)keep_prob - probability of keeping a neuron active during drop-out, scalarReturns:A3 -- last activation value, output of the forward propagation, of shape (1,1)cache -- tuple, information stored for computing the backward propagation"""np.random.seed(1)# retrieve parametersW1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]W3 = parameters["W3"]b3 = parameters["b3"]#原文有縮進問題，請注意！# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOIDZ1 = np.dot(W1, X) + b1A1 = relu(Z1)### START CODE HERE ### (approx. 4 lines)         # Steps 1-4 below correspond to the Steps 1-4 described above. # Step 1: initialize matrix D1 = np.random.rand(..., ...)#rand是隨機生成0~1之間的數D1 = np.random.rand(A1.shape[0],A1.shape[1])# Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)D1 = D1<keep_prob# Step 3: shut down some neurons of A1A1 = A1*D1# Step 4: scale the value of neurons that haven't been shut downA1/=keep_prob### END CODE HERE ###Z2 = np.dot(W2, A1) + b2A2 = relu(Z2)### START CODE HERE ### (approx. 4 lines)# Step 1: initialize matrix D2 = np.random.rand(..., ...)D2 = np.random.rand(A2.shape[0],A2.shape[1])# Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)D2 = D2<keep_prob# Step 3: shut down some neurons of A2A2 = A2*D2# Step 4: scale the value of neurons that haven't been shut downA2/=keep_prob### END CODE HERE ####輸出層只有一層，無需dropout,再dropout就沒意思了 ^_^Z3 = np.dot(W3, A2) + b3A3 = sigmoid(Z3)cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)return A3, cache

? ? ? ? Dropout的逆向傳播代碼實現:

# GRADED FUNCTION: backward_propagation_with_dropoutdef backward_propagation_with_dropout(X, Y, cache, keep_prob):"""Implements the backward propagation of our baseline model to which we added dropout.Arguments:X -- input dataset, of shape (2, number of examples)Y -- "true" labels vector, of shape (output size, number of examples)cache -- cache output from forward_propagation_with_dropout()keep_prob - probability of keeping a neuron active during drop-out, scalarReturns:gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables"""m = X.shape[1](Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = 1./m * np.dot(dZ3, A2.T)db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)dA2 = np.dot(W3.T, dZ3)### START CODE HERE ### (≈ 2 lines of code)# Step 1: Apply mask D2 to shut down the same neurons as during the forward propagationdA2 = dA2*D2# Step 2: Scale the value of neurons that haven't been shut downdA2/=keep_prob### END CODE HERE ####確保A2大于0dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = 1./m * np.dot(dZ2, A1.T)db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)dA1 = np.dot(W2.T, dZ2)### START CODE HERE ### (≈ 2 lines of code)# Step 1: Apply mask D1 to shut down the same neurons as during the forward propagationdA1 = dA1*D1# Step 2: Scale the value of neurons that haven't been shut downdA1/=keep_prob### END CODE HERE ###dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = 1./m * np.dot(dZ1, X.T)db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients

? ? ? ? 代碼來源于吳恩達的課后編程作業，上述代碼實現對3層神經網絡實施dropout操作。注意dropout在每一次迭代時會拋棄一部分神經元，被遺棄的神經元無需進行正向傳播與逆向傳播。

? 3.4?過擬合的原因解釋

? ? ? ??有了對于L1正則化如何解決過擬合問題的認識，便能很好地解釋出現過擬合原因的所以然，過擬合原因的解釋如下：

訓練數據不足：訓練數據不足的反面是訓練數據充足，眾所周知，模型的訓練數據量越大，模型的預測能力越強，泛化能力也越強，為什么呢？第一，訓練數據的增多意味著數據多樣性的增多，模型自然能見多識廣，捕捉罕見樣本，涵蓋更廣泛的場景；第二，當模型的復雜程度一定時，它學習特征與模式的能力也有限，當數據量很大時，模型自然無法對每個數據進行精細化的學習，為了降低損失函數數值，它只能在大量的數據中學習樣本的普遍特征，就好比如當樣本中有上億種貓的膚色時，模型學習這種特定特征的能力就有限了，因為它覺得去學習普遍特征更加值得，從而模型的泛化能力較強。反之亦然，當訓練的數據量較少時，模型便容易出現過擬合現象，道理都是互通的。（注：此處內容來源于在閱讀其他資料后思考得出的見解）
模型網絡過于復雜：同理，當思考復雜的模型網絡會引發過擬合前，，也需要控制其他變量，當數據量一定時，模型網絡結構過于復雜，它的特征識別能力也就過強了。（例如，小樣本訓練復雜模型）當機器“學有余力”時，它便會去提取數據特定的特征（例如，去學習貓的膚色），過度適應訓練樣本，導致在新數據上缺乏泛化能力。
模型參數過多且權重過大：道理都是互通的，當模型參數過多且權重過大時往往意味著模型網絡結構過于復雜，自然會導致過擬合。
數據特征選擇不當：道理都是互通的，訓練時模型選擇了不當的特征，比如選擇了事物的非普遍性特征，便會在預測新數據時出現過擬合問題。

? ? ??