目錄

?

基礎堆排序

一、概念及其介紹

二、適用說明

三、過程圖示

四、Java 實例代碼

src/runoob/heap/Heapify.java 文件代碼：

---

?

基礎堆排序

一、概念及其介紹

堆排序（Heapsort）是指利用堆這種數據結構所設計的一種排序算法。

堆是一個近似 完全二叉樹的結構，并同時滿足堆積的性質：即子結點的鍵值或索引總是小于（或者大于）它的父節點。

二、適用說明

我們之前構造堆的過程是一個個數據調用 insert 方法使用 shift up 逐個插入到堆中，這個算法的時候時間復雜度是 O(nlogn)，本小節介紹的一種構造堆排序的過程，稱為 Heapify，算法時間復雜度為 O(n)。

三、過程圖示

完全二叉樹有個重要性質，對于第一個非葉子節點的索引是 n/2 取整數得到的索引值，其中 n 是元素個數(前提是數組索引從 1 開始計算)。

?

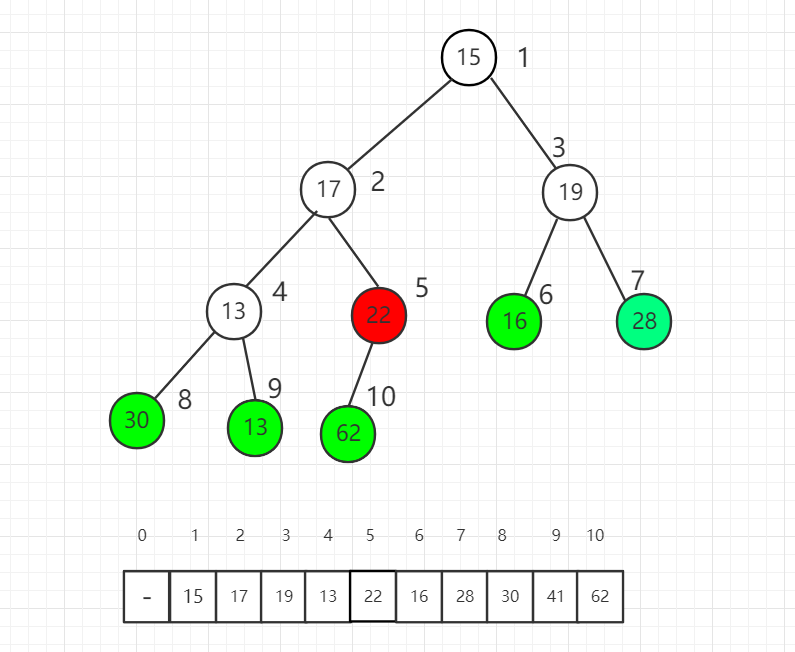
索引 5 位置是第一個非葉子節點，我們從它開始逐一向前分別把每個元素作為根節點進行 shift down 操作滿足最大堆的性質。

索引 5 位置進行 shift down 操作后，22 和 62 交換位置。

?

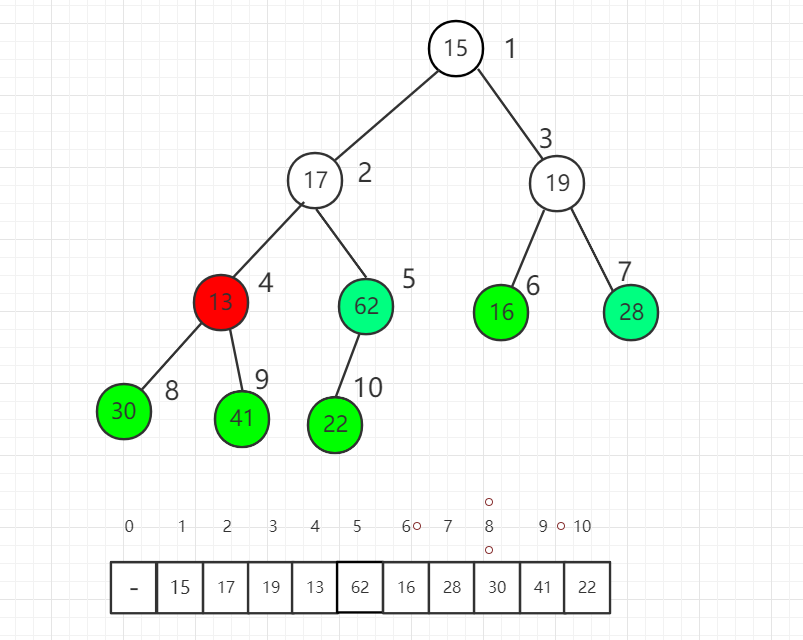
對索引 4 元素進行 shift down 操作

?

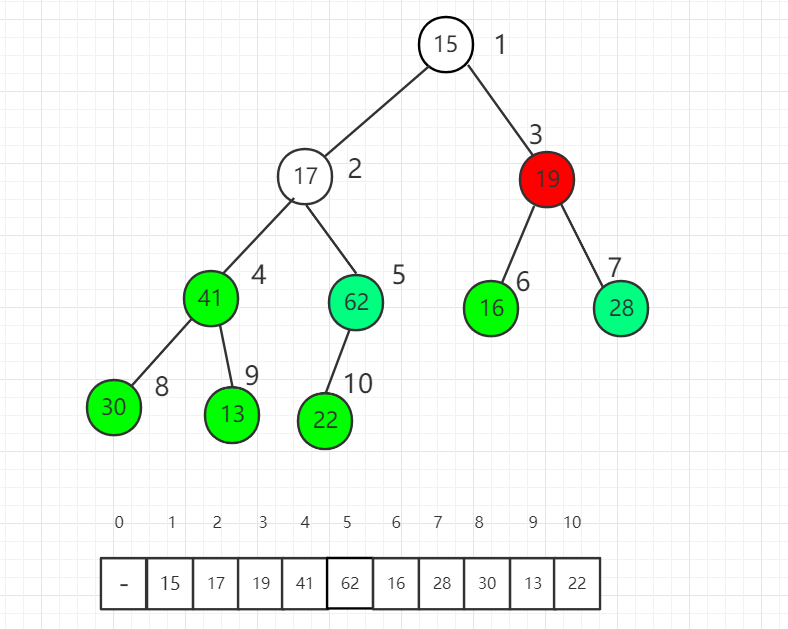
對索引 3 元素進行 shift down 操作

?

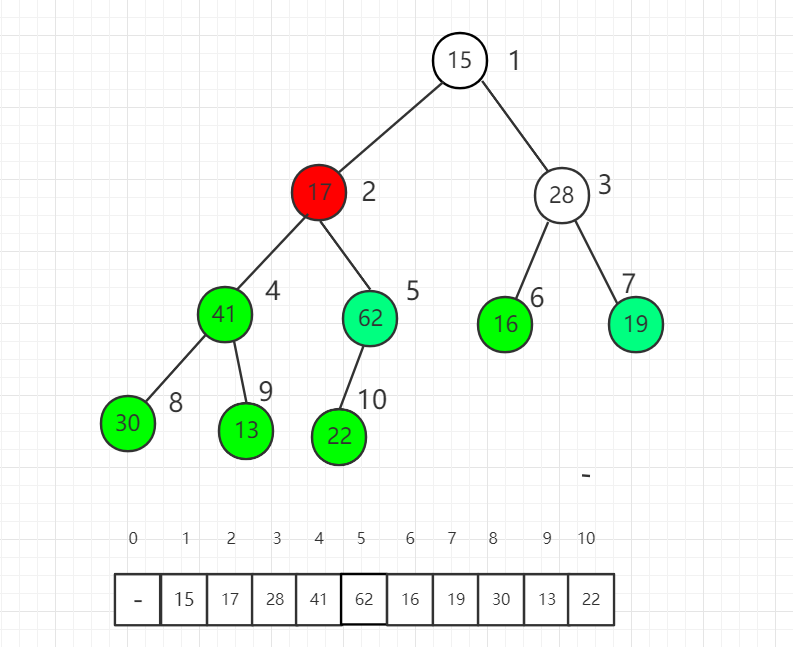
對索引 2 元素進行 shift down 操作

?

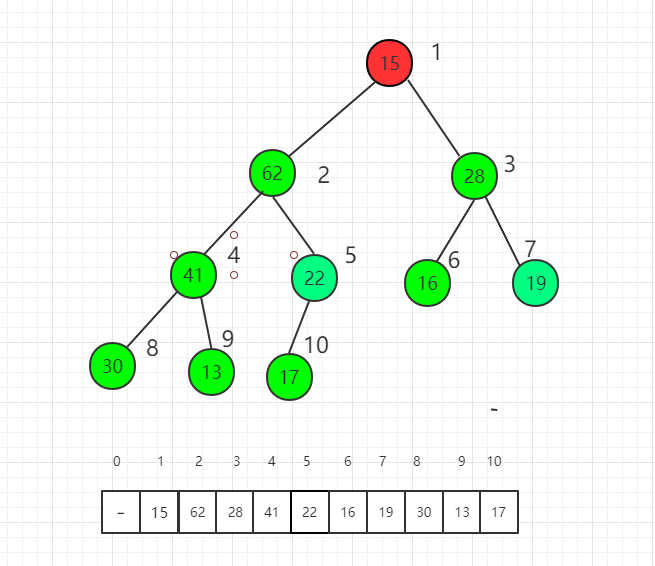
最后對根節點進行 shift down 操作，整個堆排序過程就完成了。

?

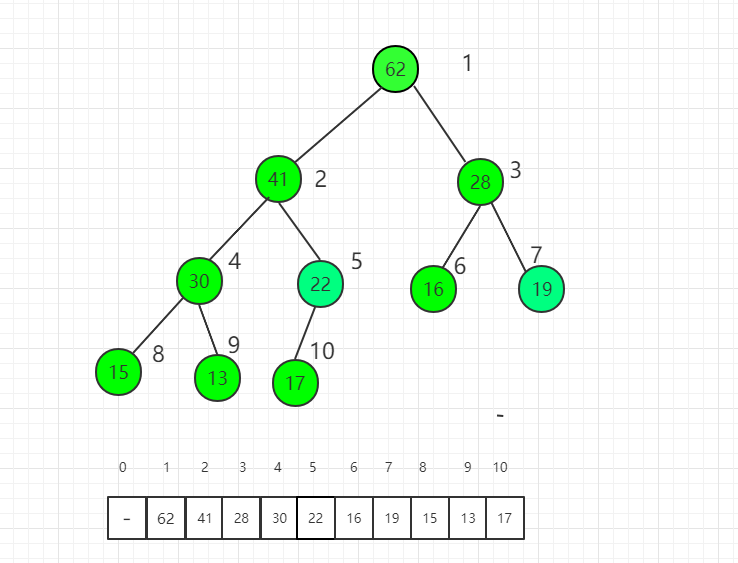
四、Java 實例代碼

源碼包下載：Downloadhttps://www.runoob.com/wp-content/uploads/2020/09/runoob-algorithm-Heapify.zip

src/runoob/heap/Heapify.java 文件代碼：

package runoob.heap;

import runoob.sort.SortTestHelper;

/**
?* 用heapify進行堆排序
?*/
public class Heapify<T extends Comparable> {

? ? protected T[] data;
? ? protected int count;
? ? protected int capacity;

? ? // 構造函數, 通過一個給定數組創建一個最大堆
? ? // 該構造堆的過程, 時間復雜度為O(n)
? ? public Heapify(T arr[]){

? ? ? ? int n = arr.length;

? ? ? ? data = (T[])new Comparable[n+1];
? ? ? ? capacity = n;

? ? ? ? for( int i = 0 ; i < n ; i ++ )
? ? ? ? ? ? data[i+1] = arr[i];
? ? ? ? count = n;
? ? ? ? //從第一個不是葉子節點的元素開始
? ? ? ? for( int i = count/2 ; i >= 1 ; i -- )
? ? ? ? ? ? shiftDown(i);
? ? }
? ? // 返回堆中的元素個數
? ? public int size(){
? ? ? ? return count;
? ? }
? ? // 返回一個布爾值, 表示堆中是否為空
? ? public boolean isEmpty(){
? ? ? ? return count == 0;
? ? }
? ? // 像最大堆中插入一個新的元素 item
? ? public void insert(T item){
? ? ? ? assert count + 1 <= capacity;
? ? ? ? data[count+1] = item;
? ? ? ? count ++;
? ? ? ? shiftUp(count);
? ? }
? ? // 從最大堆中取出堆頂元素, 即堆中所存儲的最大數據
? ? public T extractMax(){
? ? ? ? assert count > 0;
? ? ? ? T ret = data[1];
? ? ? ? swap( 1 , count );
? ? ? ? count --;
? ? ? ? shiftDown(1);
? ? ? ? return ret;
? ? }
? ? // 獲取最大堆中的堆頂元素
? ? public T getMax(){
? ? ? ? assert( count > 0 );
? ? ? ? return data[1];
? ? }


? ? // 交換堆中索引為i和j的兩個元素
? ? private void swap(int i, int j){
? ? ? ? T t = data[i];
? ? ? ? data[i] = data[j];
? ? ? ? data[j] = t;
? ? }

? ? //********************
? ? //* 最大堆核心輔助函數
? ? //********************
? ? private void shiftUp(int k){

? ? ? ? while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
? ? ? ? ? ? swap(k, k/2);
? ? ? ? ? ? k /= 2;
? ? ? ? }
? ? }

? ? private void shiftDown(int k){

? ? ? ? while( 2*k <= count ){
? ? ? ? ? ? int j = 2*k; // 在此輪循環中,data[k]和data[j]交換位置
? ? ? ? ? ? if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
? ? ? ? ? ? ? ? j ++;
? ? ? ? ? ? // data[j] 是 data[2*k]和data[2*k+1]中的最大值

? ? ? ? ? ? if( data[k].compareTo(data[j]) >= 0 ) break;
? ? ? ? ? ? swap(k, j);
? ? ? ? ? ? k = j;
? ? ? ? }
? ? }

? ? // 測試 heapify
? ? public static void main(String[] args) {
? ? ? ? int N = 100;
? ? ? ? Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
? ? ? ? Heapify<Integer> heapify = new Heapify<Integer>(arr);
? ? ? ? // 將heapify中的數據逐漸使用extractMax取出來
? ? ? ? // 取出來的順序應該是按照從大到小的順序取出來的
? ? ? ? for( int i = 0 ; i < N ; i ++ ){
? ? ? ? ? ? arr[i] = heapify.extractMax();
? ? ? ? ? ? System.out.print(arr[i] + " ");
? ? ? ? }

? ? ? ? // 確保arr數組是從大到小排列的
? ? ? ? for( int i = 1 ; i < N ; i ++ )
? ? ? ? ? ? assert arr[i-1] >= arr[i];
? ? }
}

?