一、數據類型詳細介紹

1、數據類型介紹

（1）基本的內置類型

//內置類型就是C語言自帶的類型char ? ? ? ?//字符數據類型
short ? ? ? //短整型
int ? ? ? ? //整形
long ? ? ? ?//長整型
long long ? //更長的整形
float ? ? ? //單精度浮點數
double ? ? ?//雙精度浮點數

注：C語言中沒有字符串類型。

（2）類型的意義

• 使用這個類型開辟內存空間的大小（大小決定了使用范圍）。
• 如何看待內存空間的視角。

---

2、類型的基本歸類?

（1）整型

charunsigned charsigned charshortunsigned short [int]signed short [int]intunsigned intsigned intlongunsigned long [int]signed long [int]

（2）浮點數

float
double

（3）構造類型

> 數組類型
> 結構體類型 struct
> 枚舉類型 enum
> 聯合類型 union

（4）指針類型

int* pi;
char* pc;
float* pf;
void* pv;

（5）空類型

void表示空類型（無類型）

通常應用于函數的返回類型、函數的參數、指針類型

---

二、整型在內存中的存儲

?原碼、反碼、補碼

計算機中的有符號數有三種表示方法，即原碼、反碼和補碼。

三種表示方法均有符號位和數值位兩部分，符號位都是用 0 表示 “正”，用 1 表示 “負”，而數值位三種表示方法各不相同。

?原碼

直接將二進制按照正負數的形式翻譯成二進制就可以。

?反碼

將原碼的符號位不變，其他位依次按位取反就可以得到了。

?補碼

反碼 +1 就得到補碼。

---

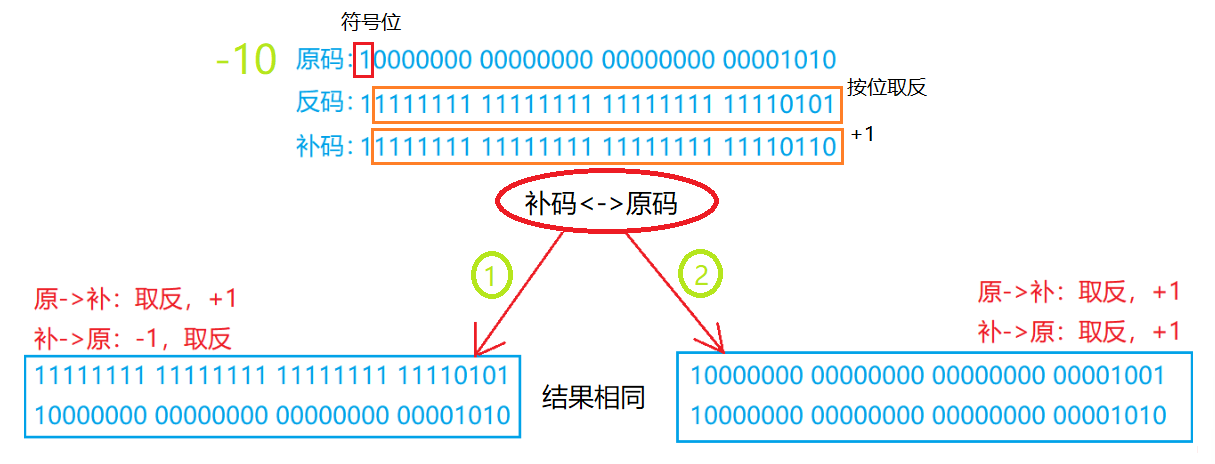
?正數的原、反、補碼都相同。

---

對于整形來說：數據存放內存中其實存放的是補碼。

在內存中的存儲：?

?

?

補碼：1111 1111 1111 1111?1111 1111 1111 0110 （-10的補碼）

f? ? ? ? f? ? ?? f? ? ? ?f? ? ? ?f? ? ? ? f? ? ? ?f? ? ? 6（-10的十六進制）

我們可以看到對于 a 和 b 分別存儲的是補碼。但是我們發現順序有點 不對勁， ?這是為什么呢？

---

三、大小端介紹

1、什么是大小端

• 大端（存儲）模式，是指數據的低位保存在內存的高地址中，而數據的高位，保存在內存的低地址中。
• 小端（存儲）模式，是指數據的低位保存在內存的低地址中，而數據的高位,，保存在內存的高地址中。

?

---

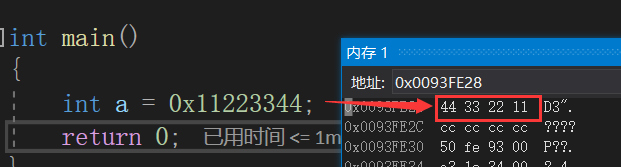2、為什么會有大端和小端呢？?

????????這是因為在計算機系統中，是以字節為單位的，每個地址單元都對應著一個字節，一個字節為 8 bit。但是在? C? 語言中除了? 8bit? 的? char? 之外，還有? 16bit? 的? short? 型， 32bit? 的? long? 型（要看具體的編譯器）。另外，對于位數大于 8? 位的處理器，例如? 16? 位或者? 32? 位的處理器，由于寄存器寬度大于一個字節，那么必然存在著一個如果將多個字節安排的問題。因此就導致了大端存儲模式和小端存儲模式。

????????例如一個 16bit 的 short 型 x ，在內存中的地址為 0x0010 ， x 的值為 0x1122 ，那么 0x11 為高字節， 0x22 為低字節。對于大端模式，就將 0x11 放在低地址中，即 0x0010 中， 0x22 放在高地址中，即 0x0011 中。小端模式，剛好相反。我們常用的 X86 結構是小端模式，而 KEIL C51 則為大端模式。很多的 ARM ， DSP 都為小端模式。有些ARM 處理器還可以由硬件來選擇是大端模式還是小端模式。

---

下面這段代碼會輸出什么呢？?

#include <stdio.h>int main()
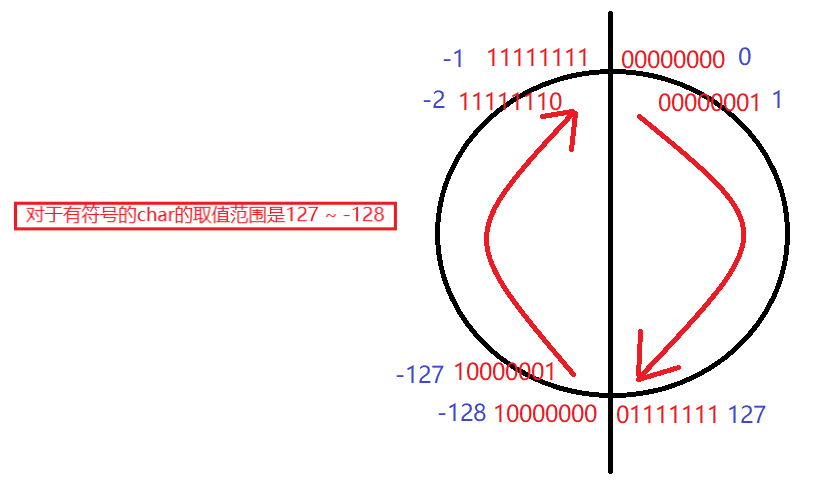
{char a= -1;signed char b=-1;unsigned char c=-1;printf("a=%d,b=%d,c=%d",a,b,c);return 0;
}

?

幫助理解：?

注：char 是 signed char 還是 unsigned char。C 語言并沒有規定，取決于編譯器(大多數編譯器下是 signed char)。

---

四、浮點型在內存中的存儲

1、常見的浮點數

3.14159 1E10 浮點數家族包括： float 、 double 、 long double 類型。

浮點數表示的范圍： float.h 中定義。????????????

---

2、標準規定?

根據國際標準?IEEE（電氣和電子工程協會） 754，任意一個二進制浮點數V可以表示成下面的形式（了解即可）：

• (-1)^S * M * 2^E
• (-1)^S?表示符號位，當 S=0，V為正數；當 S=1，V為負數。
• M?表示有效數字，大于等于1，小于2。
• 2^E?表示指數位。

舉例來說：

十進制的? 5.0 ，寫成二進制是 101.0 ，相當于 1.01×2^2 。 那么，按照上面 V 的格式，可以得出S =0 ，M=1.01， E=2 。

十進制的? -5.0 ，寫成二進制是 - 101.0 ，相當于 - 1.01×2^2 。那么，S =1 ， M=1.01 ， E=2 。

IEEE 754 規定：

對于? 32? 位的浮點數， 最高的?1?位是符號位 S，接著的?8?位是指數?E，剩下的?23?位為有效數字M 。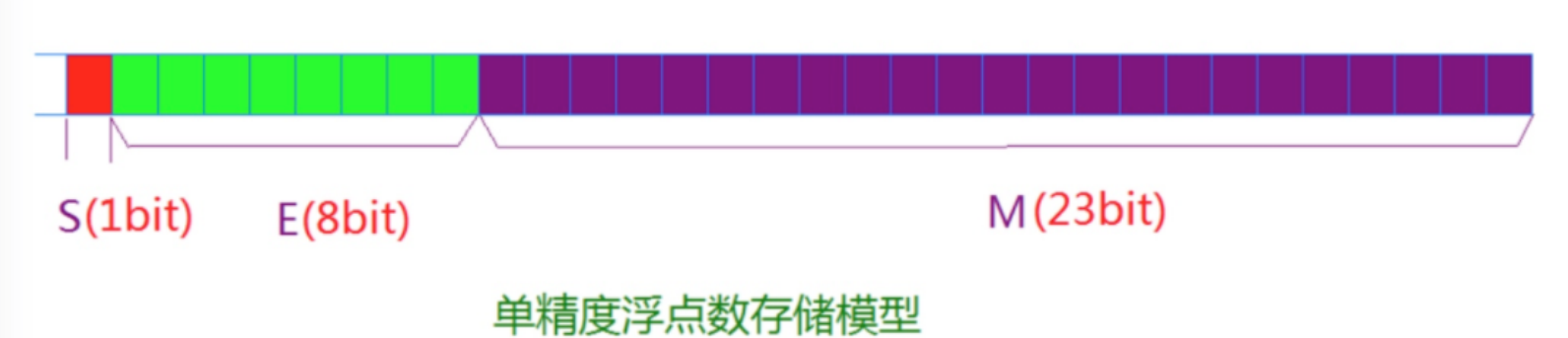

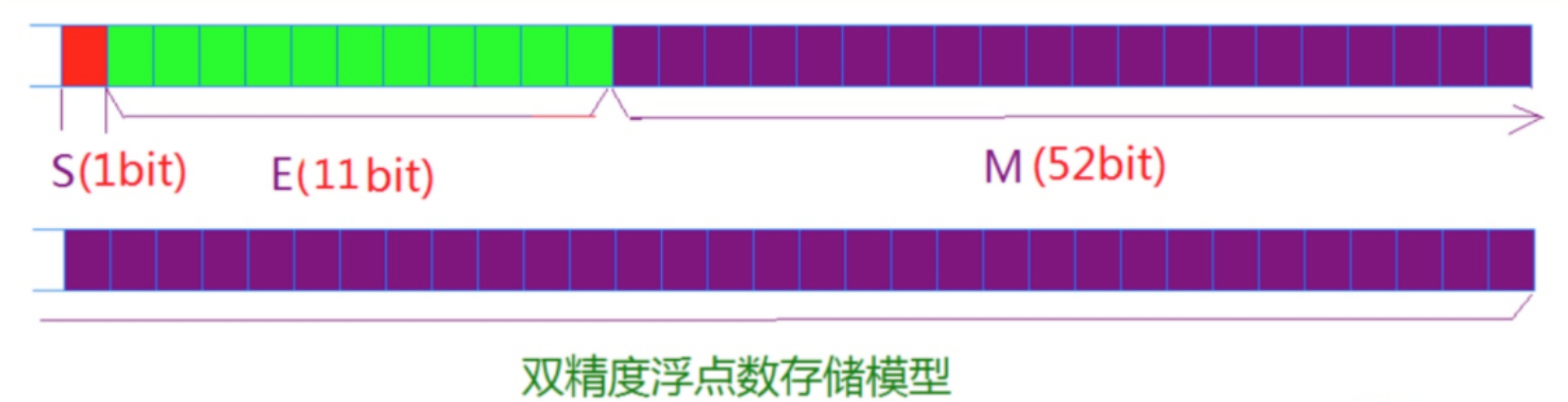
對于64位的浮點數，最高的1位是符號位S，接著的11位是指數E，剩下的52位為有效數字M。

?E全為1

這時，如果有效數字 M 全為 0，表示 ±無窮大（正負取決于符號位S）；

---

浮點數存儲的例子：

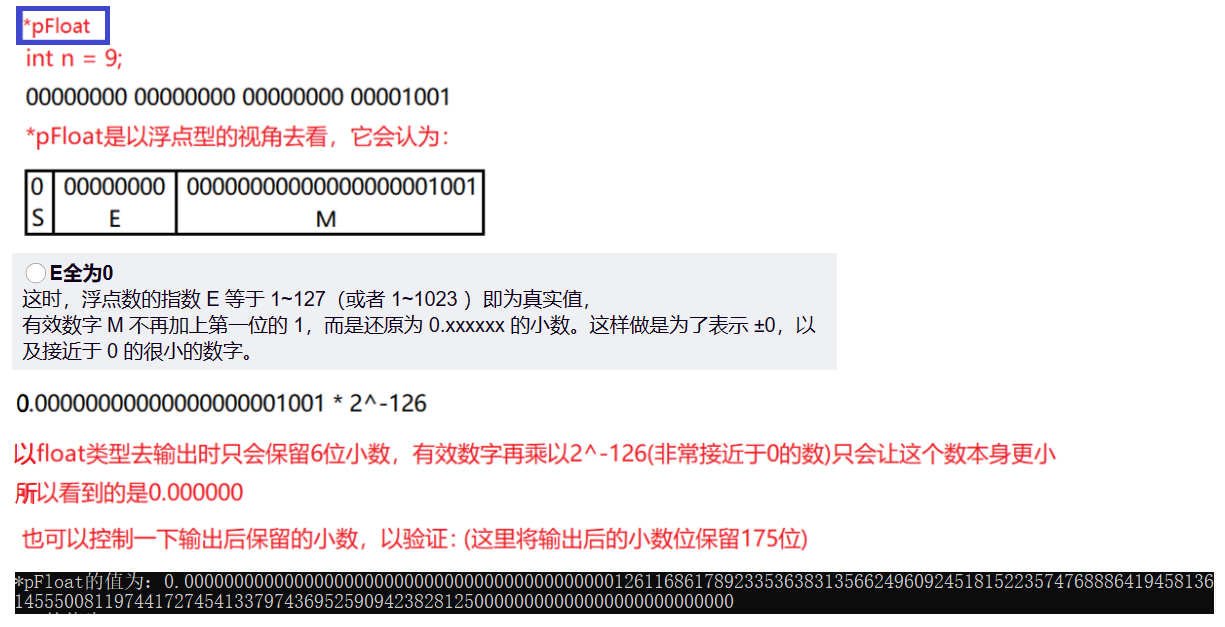
int main()
{int n = 9; //以整型的視角放入float *pFloat = (float *)&n;printf("n的值為：%d\n",n); //以整型的視角拿出printf("*pFloat的值為：%f\n",*pFloat); //以浮點型的視角拿出*pFloat = 9.0; //以浮點型的視角放入printf("num的值為：%d\n",n); //以整型的視角拿出printf("*pFloat的值為：%f\n",*pFloat); //以浮點型的視角拿出return 0;
}

?

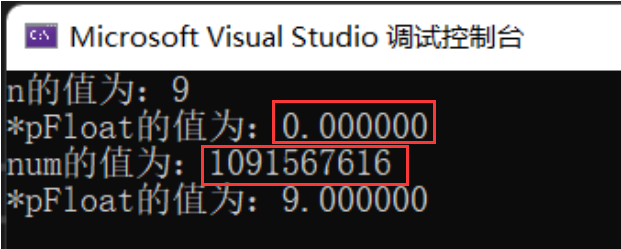?num 和 *pFloat 在內存中明明是同一個數，為什么浮點數和整數的解讀結果會差別這么大？

?分析如下：

?