1. 邏輯回歸

邏輯回歸（Logistic Regression）的模型是一個非線性模型，

sigmoid函數，又稱邏輯回歸函數。但是它本質上又是一個線性回歸模型，因為除去sigmoid映射函

數關系，其他的步驟，算法都是線性回歸的。

可以說，邏輯回歸，都是以線性回歸為理論支持的。

只不過，線性模型，無法做到sigmoid的非線性形式，sigmoid可以輕松處理0／1分類問題。

? ? ? ?首先，找一個合適的預測函數，一般表示為h函數，該函數就是需要找的分類函數，它用來預

測輸入數據的判斷結果。然后，構造一個Cost函數（損失函數），該函數表示預測的輸出（h）與

訓練數據類別（y）之間的偏差，可以是二者之間的差（h—y）或者是其他的形式。綜合考慮所有

訓練數據的“損失”，將Cost求和或者求平均，記為J（θ）函數，表示所有訓練數據預測值與實際類

別的偏差。顯然，J（θ）函數的值越小表示預測函數越準確（即h函數越準確），所以這一步需要

做的是找到J（θ）函數的最小值。找函數的最小值有不同的方法，Logistic Regression實現時有的

是梯度下降法（Gradient Descent )。

2. 二分類問題

二分類問題是指預測的y值只有兩個取值（0或1），二分類問題可以擴展到多分類問題。例如：我

們要做一個垃圾郵件過濾系統，x是郵件的特征，預測的y值就是郵件的類別，是垃圾郵件還是正常

郵件。對于類別我們通常稱為正類（positive class）和負類（negative class），垃圾郵件的例子

中，正類就是正常郵件，負類就是垃圾郵件。

應用舉例：是否垃圾郵件分類？是否腫瘤、癌癥診斷？是否金融欺詐？

3. logistic函數

如果忽略二分類問題中y的取值是一個離散的取值（0或1），我們繼續使用線性回歸來預測y的取

值。這樣做會導致y的取值并不為0或1。邏輯回歸使用一個函數來歸一化y值，使y的取值在區間

（0，1）內，這個函數稱為Logistic函數（logistic function），也稱為Sigmoid函數（sigmoid

function）。函數公式如下：

Logistic函數當z趨近于無窮大時，g（z）趨近于1；當z趨近于無窮小時，g（z）趨近于0。Logistic

函數的圖形如下：

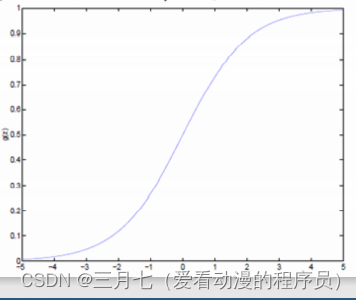
線性回歸模型幫助我們用最簡單的線性方程實現了對數據的擬合，然而，這只能完成回歸任務，無

法完成分類任務，那么 logistics regression 就是在線性回歸的基礎上添磚加瓦，構建出了一種分類

模型。如果在線性模型的基礎上做分類，比如二分類任務，即：y取值{0，1}，

最直觀的，可以將線性模型的輸出值再套上一個函數y = g（z），最簡單的就是“單位階躍函數”

（unit—step function），如下圖中紅色線段所示。

也就是把看作為一個分割線，大于 z 的判定為類別0，小于 z 的判定為類別1。

但是，這樣的分段函數數學性質不太好，它既不連續也不可微。通常在做優化任務時，目標函數最

好是連續可微的。這里就用到了對數幾率函數（形狀如圖中黑色曲線所示）。

它是一種"Sigmoid”函數，Sigmoid函數這個名詞是表示形式S形的函數，對數幾率函數就是其中最

重要的代表。這個函數相比前面的分段函數，具有非常好的數學性質，其主要優勢如下：使用該函

數做分類問題時，不僅可以預測出類別，還能夠得到近似概率預測。這點對很多需要利用概率輔助

決策的任務很有用。對數幾率函數是任意階可導函數，它有著很好的數學性質，很多數值優化算法

都可以直接用于求取最優解。

總的來說，模型的完全形式如下：，LR模型就是在擬合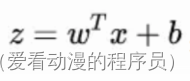

這條直線，使得這條直線盡可能地將原始數據中的兩個類別正確的劃分開。

對于線性邊界的情況，邊界形式如下：

構造預測函數為:

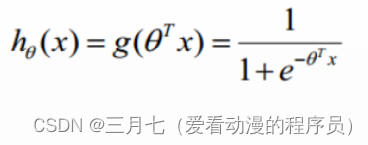
h(x)的值有特殊的含義，它表示結果取1的概率，因此對于輸入x分類結果為類別1和類別0的概率分

別為：

正例(y=1)? ?

負例(y=0)? ?

4. 損失函數

對于任何機器學習問題，都需要先明確損失函數，LR模型也不例外，在遇到回歸問題時，通常我

們會直接想到如下的損失函數形式（平均誤差平方損失MSE)：

但在LR模型要解決的二分類問題中，損失函數的形式是這樣的：

這個損失函數通常稱作為對數損失(logloss),這里的對數底為自然對數e，其中真實值 y 是有 0/1 兩

種情況，而推測值由于借助對數幾率函數，其輸出是介于0~1之間連續概率值。仔細查看，不難發

現，當真實值y=0時，第一項為0，當真實值y=1時，第二項為0，所以，這個損失函數其實在每次

計算時永遠都只有一項在發揮作用，那這就可以轉換為分段函數，分段的形式如下：

5. 優化求解?

現在我們已經確定了模型的損失函數，那么接下來就是根據這個損失函數，不斷優化模型參數從而

獲得擬合數據的最佳模型。

重新看一下損失函數，其本質上是 L 關于模型中線性方程部分的兩個參數 w?和 b 的函數：

?其中，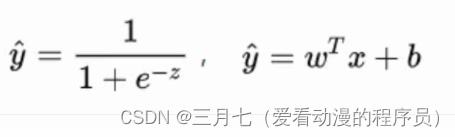

現在的學習任務轉化為數學優化的形式即為：

由于損失函數連續可微，我們可以借助梯度下降法進行優化求解，對于兩個核心參數的更新方式如

下：?

求得：

進而求得：

轉換為矩陣的計算方式為：

至此，?Logistic Regression模型的優化過程介紹完畢。

6. 梯度下降算法

梯度下降法求J（θ）的最小值，θ的更新過程：

要使得最大化，則運用梯度上升法，求出最高點：

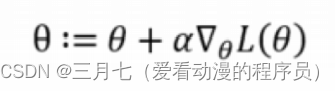
# 梯度上升，主要是采用了最大似然的推導
def gradAscent(dataMatIn,classLabels):dataMatrix = mat(dataMatIn)labelMat = mat(classLabels).transpose()m,n = shape(dataMatrix)  # n=3alpha=0.001  # 學習率maxCycles=500  # 循環輪數theta = ones((n,1))for k in range(maxCycles):h=sigmoid(dataMatrix * theta)error = (labelMat - h)theta = theta + alpha * dataMatrix.transpose()*errorreturn theta

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?

?