二叉搜索樹K和KV結構模擬

一什么是二叉搜索樹

? 這個的結構特性非常重要，是后面函數實現的結構基礎，二叉搜索樹的特性是每個根節點都比自己的左樹任一節點大，比自己的右樹任一節點小。

例如這個圖，

?41是根節點，要比左樹大，比右樹小，滿足但還不夠，還要去看看41的左子樹的根和右子樹的根是否滿足，更要判斷這棵樹上所有的根節點是不是都滿足。而這棵樹最厲害的地方之一我們用中序遍歷(順序左根右)便可以知道，遍歷結果為13,15,17,22,28,33,37,41,42,50,53,58,61,66,78，排序不就排好了嗎，復雜度可媲美快排和歸并。二叉搜索樹另一個功能那當然就是搜索了，例如我們要找66,66比根節點大，就不用去左子樹找了，一下子少遍歷一半，然后就去右子樹找，和根節點58比較，66比58大，再去右子樹找，再比較就找到了，最多查找高度次，滿二叉樹下為log(n)。而二叉搜索樹是不是完美無缺，我也以為已經完美了，不好意思，我太年輕了，直到我看到下面這顆樹。

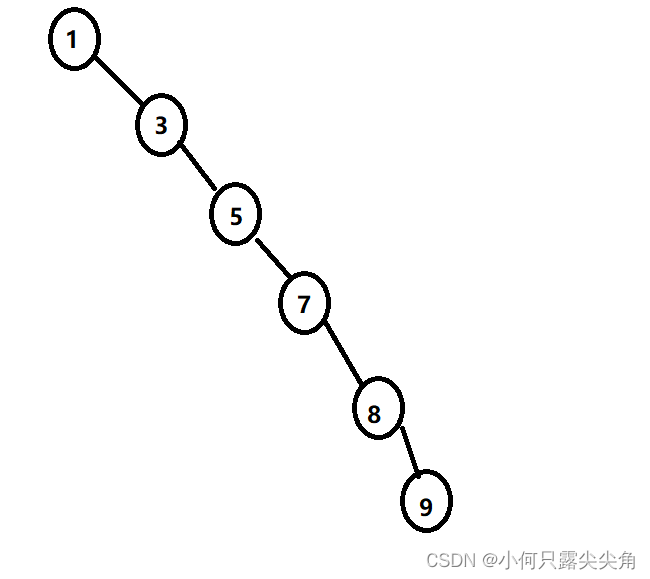
?這個查找一次的效率就退化為O(N)了，解決辦法：轉化為平衡二叉樹，通俗點就是換個根節點重新構造二叉樹，例如把5或者7換成根節點，大家可以試試練習一下構建二叉樹，構建完后的高度肯定比上圖低，查找效率不就高了嗎。

? ?在說二叉搜索樹的實現前，我們先說說什么是K結構，什么是KV結構，K結構就是只存一個數據，這個數據稱為關鍵碼，例如在英文詞庫里找一個英文單詞，就是用關鍵碼查找，需要的數據也是找到的關鍵碼，但是KV結構就不同了，例如，通過拼音找漢字，這個時候拼音就是關鍵碼，但是我們需要的數據不是拼音這個關鍵碼，而是與之對應的漢字，這就是KV結構。

二二叉搜索樹K結構實現

1 樹的節點類

template<class T>struct TreeNode{TreeNode(const T& val):_val(val)//_val可能為自定義類型，在初始化列表初始化方便調用構造函數{;}TreeNode* left = nullptr;TreeNode* right = nullptr;T _val;};

2 BinaryTree樹類

查找和排序都封裝到了BinaryTree類中，和list一樣，將節點類和樹類分開封裝。

?(1)?默認構造函數

template<class T>class BinaryTree{public:typedef TreeNode<T> Node;BinaryTree(Node*node=nullptr)  該構造函數是用節點指針初始化，也可以再寫個構造函數用個BinaryTree對象初始化:_root(node){;}private:Node* _root = nullptr;樹類只需根節點地址即可管理整棵樹};

? (2)? 拷貝構造函數

因為兩個copy函數都是用遞歸遍歷二叉樹，所以只能再寫一個子函數，畢竟外部無法傳_root指針。

void copy1(Node*tree)//前序遍歷加復用insert拷貝二叉樹{if (tree == nullptr)return;insert(tree->_val); 先插入根節點的值,再去左子樹和右子樹獲取節點的數值insert內部會開辟空間copy(tree->left);copy(tree->right);}方法二比較巧妙的是它的第一個參數,root是外部傳參_root的引用所以root=new node(),可以直接修改根節點而要拷貝左子樹就傳root->left的引用，這樣new出來的節點可以直接連接到根的_left指針上。右子樹同理。void copy2(Node*&root,Node*tree){if (tree== nullptr)return;root = new Node(tree->_val);copy2(root->left,tree->left);copy2(root->right,tree->right);}BinaryTree(const BinaryTree<T>&tree){//copy(tree._root);copy2(_root, tree._root);}

copy2函數傳指針引用我是受下面一個成員函數實現的啟發，這個傳引用一定要好好體會，方便理解后面的函數，非常巧妙。

(3)? 賦值

? ?用的是現代寫法，比如t1,t2是兩個BinaryTree對象，t1=t2就會調用下面的賦值函數，可是我的參數不是引用，那按規定自定義類型傳值傳參要用拷貝構造(我在類的成員函數博客曾提及)，t2傳參給tree就要調用拷貝構造，那tree就是一個新拷貝的對象，我們就可以用swap直接交換tree和t1的根節點指針，并且tree就是一個局部對象，函數調用完后會自動調用析構函數，省去了我們寫析構t1樹和創建新樹的功夫，都給編譯器做了。(string模擬的賦值也用到了現代寫法)

?void swap(BinaryTree<T>& tree){std::swap(_root, tree._root);}void operator=(BinaryTree<T> tree){swap(tree);}?

(4) find函數

搜索樹怎么能缺少搜索功能呢


這個是find函數的子函數，子函數原因和上面同理，都是一開始傳參外部無法獲取_root，因為遞歸遍歷代碼量少，所以我實現的是遞歸版本bool _findR(Node*root,const T& val){if (root == nullptr)return false;if (val > root->_val)//val比當前_val大，去右樹找{return _findR(root->right, val);}else if (val < root->_val)//val比當前_val小，去左樹找{return _findR(root->left, val);}else  {return true;//val和當前_val相等，返回true}}//下面這個是外部調用的find函數，只需要傳要查找的值即可  bool find(const T& val){return _findR(_root, val);}

我之前在寫find函數時，我還想著返回false是不是應該當左樹和右樹都沒找到才返回false,好一會才醒悟，我們之所以去左樹找，就是因為要找的val比根節點的值小，那右樹更不會有了，所以左樹找到nullptr就應該返回false，同理右樹找到nullptr也返回false。

(5) insert函數

因為要遞歸去找合適的位置插入，所以同樣要寫一個子函數  void _insertR(Node*& root, const T&val){if (root == nullptr)當找到空節點，就可以插入了，此時才是引用起作用的時候{root = new Node(val);  直接就可以修改了，因為root是上一個節點的left或者 right指針的引用。return;}Node* cur = root;if (val > cur->_val)//val大于當前根，插入到右樹去{_insertR(cur->right,val);}else if (val < cur->_val)//val小于當前根，插入到左樹去{_insertR(cur->left, val);}else{return;}}void insert(const T& val){_insertR(_root, val);}

(6) 中序遍歷

		void _Inorder(Node* root)//中序遞歸遍歷{if (root == nullptr)return;_Inorder(root->left);  一直往左子樹遞歸，直到左子樹為空,算訪問完，可以訪問根。cout << root->_val << " "; _Inorder(root->right); 然后去右子樹訪問，同樣分為左子樹，根，右子樹}void Inorder(){_Inorder(_root);//調用子函數,外部無法獲取私有成員_root}

(7) erase函數

     bool _Rerase(Node*&root,const T&val){if (root == nullptr)return false;Node* cur = root;if (val > root->_val)//用_val找節點{return _Rerase(root->right, val);}else if (val < root->_val){return _Rerase(root->left, val);}else//找到了{//該節點只有一個或者無子節點if (root->left == nullptr)  由于root是上一節點左指針或者右指針的別名，所以可以直接拿root->right來賦值給root，否則還要 判斷root->right是鏈接在上一節點的left指針還是 right指針。{root = root->right;}else if (root->right == nullptr){root = root->left;}else{刪除有兩個子節點的節點-替換法找該節點左子樹中最大的，或者右子樹中最小的來替換刪除節點Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}std::swap(leftMax->_val, root->_val);return _Rerase(root->left, val);調用_Rerase去刪除leftMax節點，這里必須要傳root->left，去左子樹刪除值為val的節點，不能傳root例如我們交換leftMax的7和root的8值，如果傳root,8的值比7大，就會去右樹刪，就找不到leftMax節點了，但是root的左子樹仍然滿足二叉搜索的特性，就可以找到leftMax節點并刪除。  }delete cur;  該處統一釋放刪除節點，并返回truereturn true;}}bool erase(const T& val)//刪除某個節點{return _Rerase(_root, val);}

三 kv結構實現

? ?本來我以為kv結構是要將K結構的樹大改，當我實現后才發現，賦值可以直接照搬，，find,insert，erase中大量的if判斷都是用關鍵碼判斷，根本不需要改動，中序遍歷也就多打印一個數據，還有insert和拷貝構造函數要在new一個節點的時候多傳一個參數。

接下來就看看一些比較重要的改動，在這里_key存關鍵碼，而我上面二叉樹K結構中是_val存的關鍵碼，不要搞混了。

1 樹的節點類

     template<class T,class K>struct TreeNode{TreeNode(const T& val,const K&key):_val(val),_key(key){;}             類內可不加模板參數，也就是說TreeNode等價于TreeNode<T,k>TreeNode* left = nullptr; TreeNode* right = nullptr;T _val;//存與關鍵碼對應的數據K _key;//_key存關鍵碼};

2 BinaryTree類

有了先前K結構樹的基礎，這里構造和析構函數我們就很好理解。

(1)構造和析構函數

template<class T, class K>class BinaryTree{public:typedef TreeNode<T,K> Node;BinaryTree(Node* node = nullptr)  默認構造無改變:_root(node){;}void _DestroyR(Node*&root)  遞歸釋放節點，采用后序遍歷的方式delete{if (root == nullptr)return;_DestroyR(root->left);_DestroyR(root->right);delete root;root = nullptr;}~BinaryTree(){_DestroyR(_root);}private:Node* _root = nullptr;   成員變量是不變的，畢竟kv結構的樹用根節點同樣可以管理};
}

(3)erase函數

  bool _Rerase(Node*& root, const T& key){if (root == nullptr)return false;Node* cur = root; //記錄節點，方便后面deleteif (key > root->_key){return _Rerase(root->right,key);}else if (key <root->_key){return _Rerase(root->left, key);}else//找到了{//該節點只有一個或者無子節點if (root->left == nullptr){root = root->right;}else if (root->right == nullptr){root = root->left;}else{Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}std::swap(leftMax->_val, root->_val); 在交換時要多交換一個值std::swap(leftMax->_key, root->_key);return _Rerase(root->left, key); 并且還是用key值去找leftMax刪}  刪除完leftMax后就直接return了，就不會重復刪除。delete cur;return true;}}bool erase(const T& val)//刪除某個節點{return _Rerase(_root, val);}

二叉搜索樹中最復雜的就是erase函數，大家在此處一定要畫圖理解。