💓博主個人主頁:不是笨小孩👀
?專欄分類:數據結構與算法👀 刷題專欄👀 C語言👀
🚚代碼倉庫:笨小孩的代碼庫👀
?社區:不是笨小孩👀
🌹歡迎大家三連關注,一起學習,一起進步!!💓

二叉樹
- 二叉樹的性質
- 二叉樹的鏈式結構
- 二叉樹的遍歷
- 前序遍歷
- 中序遍歷
- 后序遍歷
- 層序遍歷
- 二叉樹的銷毀
- 二叉樹的查找
二叉樹的性質
1.若規定根節點的層數為1,則一棵非空二叉樹的第i層上最多有2^(i-1) 個結點.
2. 若規定根節點的層數為1,則深度為h的二叉樹的最大結點數是 2^h-1.
3. 對任何一棵二叉樹, 如果度為0其葉結點個數為n0 , 度為2的分支結點個數為02 ,則有n0 =n2 +1
4. 若規定根節點的層數為1,具有n個結點的滿二叉樹的深度,h= . (ps: 是log以2為底,n+1為對數)
5. 對于具有n個結點的完全二叉樹,如果按照從上至下從左至右的數組順序對所有節點從0開始編號,則對于序號為i的結點有:
- 若i>0,i位置節點的雙親序號:(i-1)/2;i=0,i為根節點編號,無雙親節點
- 若2i+1<n,左孩子序號:2i+1,2i+1>=n否則無左孩子
- 若2i+2<n,右孩子序號:2i+2,2i+2>=n否則無右孩子
二叉樹的鏈式結構
一般來說,二叉樹分為二叉鏈和三叉鏈,二叉鏈就是結構里面一個左孩子節點,一個右孩子節點,三叉鏈多了一個父親節點,我們比較經常見的都是二叉鏈的,所以我們主要講的也是二叉鏈。
結構:
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;我們在看任意一顆二叉樹時,都可以將它分為三部分,根,左子樹,右子樹,左子樹也可看成根,左子樹,右子樹,右子樹也可看成根,左子樹,右子樹,因此二叉樹定義是遞歸式的,我們后面的代碼也是主要靠遞歸來實現的。
二叉樹的遍歷
二叉樹遍歷(Traversal)是按照某種特定的規則,依次對二叉樹中的節點進行相應的操作,并且每個節點只操作一次。
二叉樹的遍歷分為,前序遍歷、中序遍歷、后序遍歷、層序遍歷,其中前中后序遍歷是遞歸定義的,而層序遍歷是非遞歸遍歷的。
前序遍歷
前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點的操作發生在遍歷其左右子樹之前。前序先訪問根節點,再訪問左子樹,再訪問右子樹。
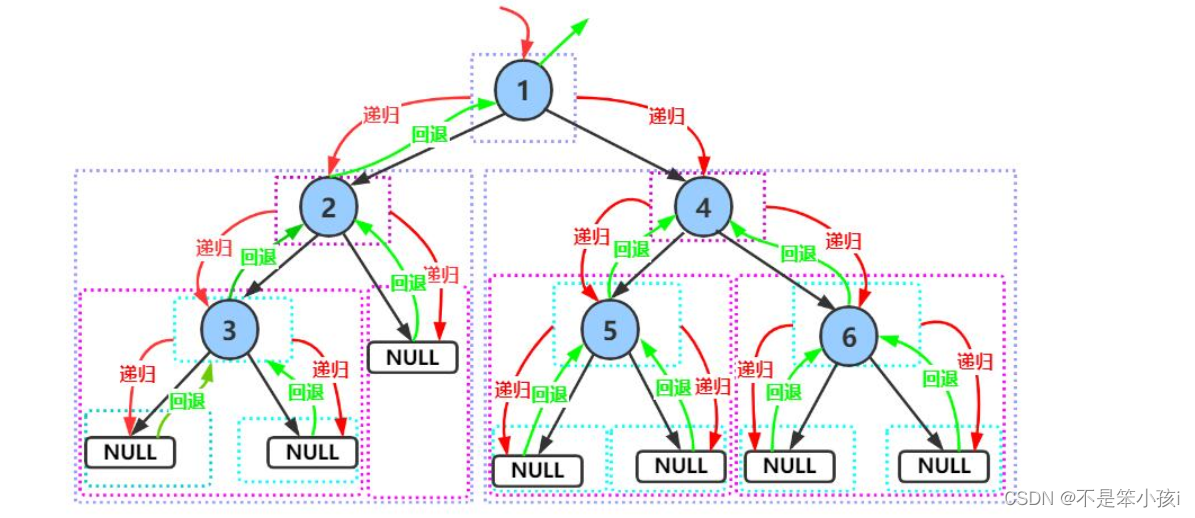
代碼如下:
// 二叉樹前序遍歷
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
遞歸圖:
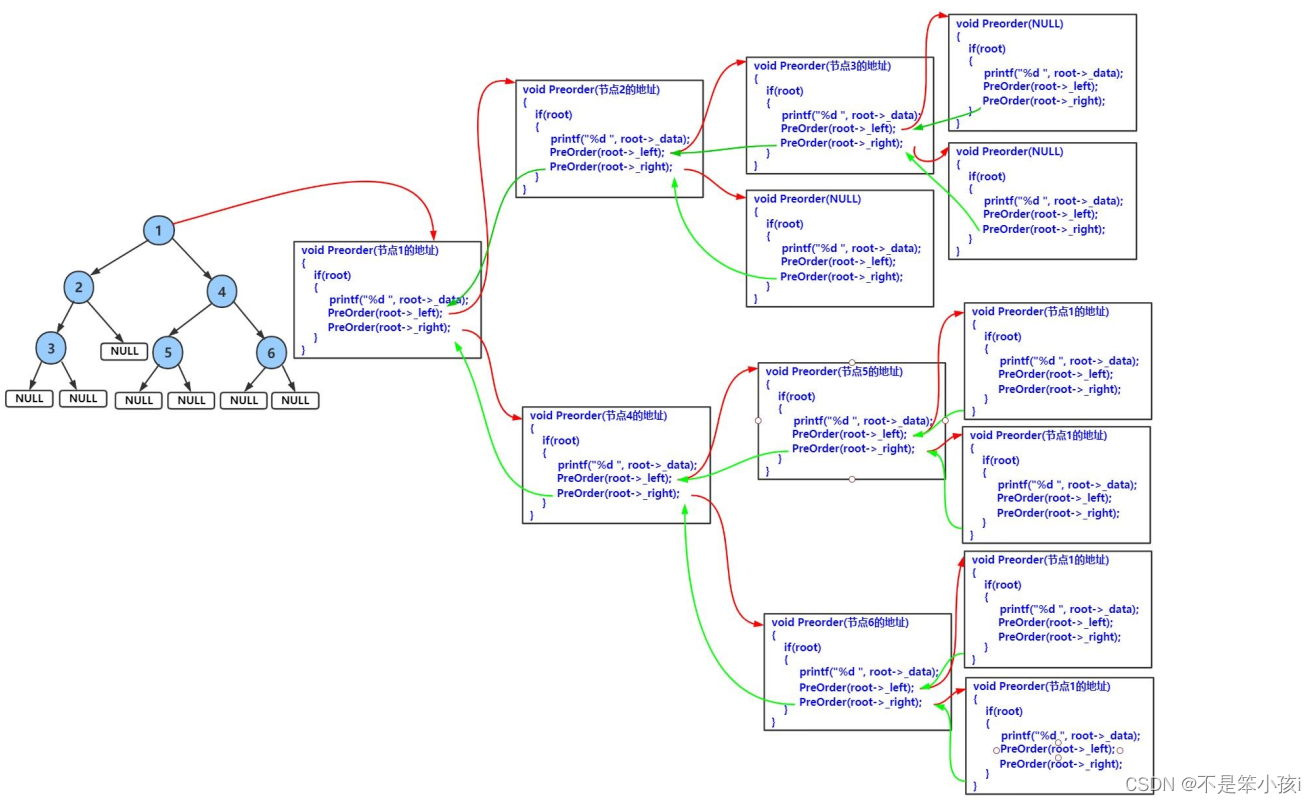
大家可以根據這個遞歸展開圖好好理解一下,后面的二叉樹基本操作都是需要用遞歸來實現的。
中序遍歷
中序遍歷(Inorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之中(間)。
代碼如下:
// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);}
后序遍歷
后序遍歷(Postorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之后。
代碼如下:
// 二叉樹后序遍歷
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}
這三種遍歷本質上都是一樣的,理解清楚一個,另外兩個就很簡單了。
層序遍歷
層序遍歷和其他三種都不一樣,設二叉樹的根節點所在層數為1,層序遍歷就是從所在二叉樹的根節點出發,首先訪問第一層的樹根節點,然后從左右訪問第2層上的節點,接著是第三層的節點,以此類推,自上而下,自左至右逐層訪問樹的結點的過程就是層序遍歷。
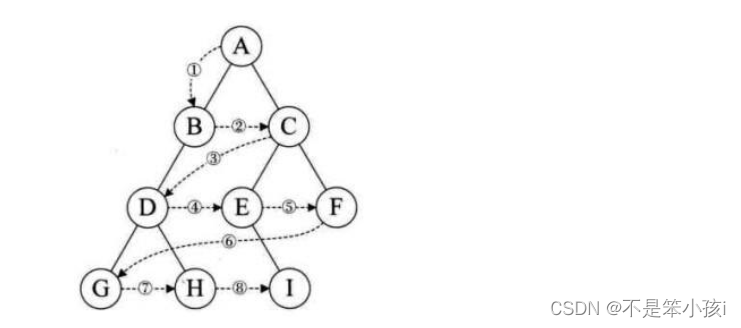
那這個要怎么實現呢?
我們需要借助我們的隊列,我們可以先把根節點入到隊列里,然后開始出隊列,只不過每次出的時候如果它的左孩子不為空就將左孩子入隊列,右孩子不為空就將右孩子入隊列,以此類推。我們就是利用了隊列的先進先出,我們就可以輕松地完成層序遍歷。
代碼如下:
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q,root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}printf("%d ", front->data);}printf("\n");
}
二叉樹的銷毀
二叉樹的銷毀很簡單,我們需要遍歷一遍二叉樹,但是我們用那種遍歷呢,如果用前序,那么就會銷毀根節點,就找不到它的左孩子和右孩子,明顯是不合適的,最好的情況就是我們先去銷毀它的左孩子,再去銷毀他的右孩子,然后再銷毀根節點,所以這里我們使用后序遍歷是比較合適的。
代碼如下:
// 二叉樹銷毀
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}
二叉樹的查找
二叉樹的查找的基本思路也是遍歷一遍二叉樹,但是我們需要返回這個節點,這就給我們的難度增加了很多,我們這里想的是先看根節點是不是,如果不是就去他的左子樹找,如果找到了就返回,否則就去它的右子樹找,找到就返回該節點,最后都找不到我們就返回NULL.
代碼如下:
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* left = BinaryTreeFind(root->left, x);if (left != NULL){return left;}BTNode* right = BinaryTreeFind(root->right, x);if (right != NULL){return right;}return NULL;
}
最后帶大家看一下會給我們帶來好運的樹:

今天的分享就到這里,感謝大家的關注和支持!



- 使用cookie避免重復登錄)




)



)






