?💥💥💞💞歡迎來到本博客????💥💥

🏆博主優勢：🌞🌞🌞博客內容盡量做到思維縝密，邏輯清晰，為了方便讀者。

??座右銘：行百里者，半于九十。

📋📋📋本文目錄如下：🎁🎁🎁

目錄

💥1 概述

📚2 運行結果

🎉3?參考文獻

🌈4 Matlab代碼實現

---

💥1 概述

在神經網絡訓練中，使用傳統的梯度下降法可能會受到局部極值問題的影響，導致訓練結果不夠穩定或收斂速度較慢。為了改進神經網絡的權值訓練，考慮結合灰狼優化（GWO）、帝國競爭算法（ICA）和粒子群優化（PSO）等優化算法。下面是方法：

初始化神經網絡： 首先，根據問題的特點和需求，設計并初始化神經網絡的結構，包括神經元層、激活函數等。

梯度下降法訓練： 使用傳統的梯度下降法對神經網絡進行初始訓練，以獲得一個基本的權值設置。

算法集成： 將灰狼優化（GWO）、帝國競爭算法（ICA）和粒子群優化（PSO）三種優化算法集成到神經網絡的權值調整過程中。

多種算法運行： 為了充分利用這些算法的優勢，可以采取以下策略：

在每次權值更新之前，使用三種算法分別對神經網絡權值進行優化，得到三組不同的權值。

將這三組權值分別代入神經網絡進行預測或訓練，得到對應的損失函數值。

根據損失函數值的大小，選擇其中表現最好的一組權值來更新神經網絡。

參數調整： 每個優化算法都有一些參數需要調整，如迭代次數、種群大小等。您可以通過實驗和交叉驗證來選擇最佳的參數組合，以達到更好的性能。

終止條件： 設置合適的終止條件，如達到一定的迭代次數或損失函數值足夠小。

結果分析： 最后，比較集成了三種優化算法的權值訓練方法與單獨使用梯度下降法的效果。分析哪種方法在收斂速度、穩定性和精度方面表現更好。

📚2 運行結果

?

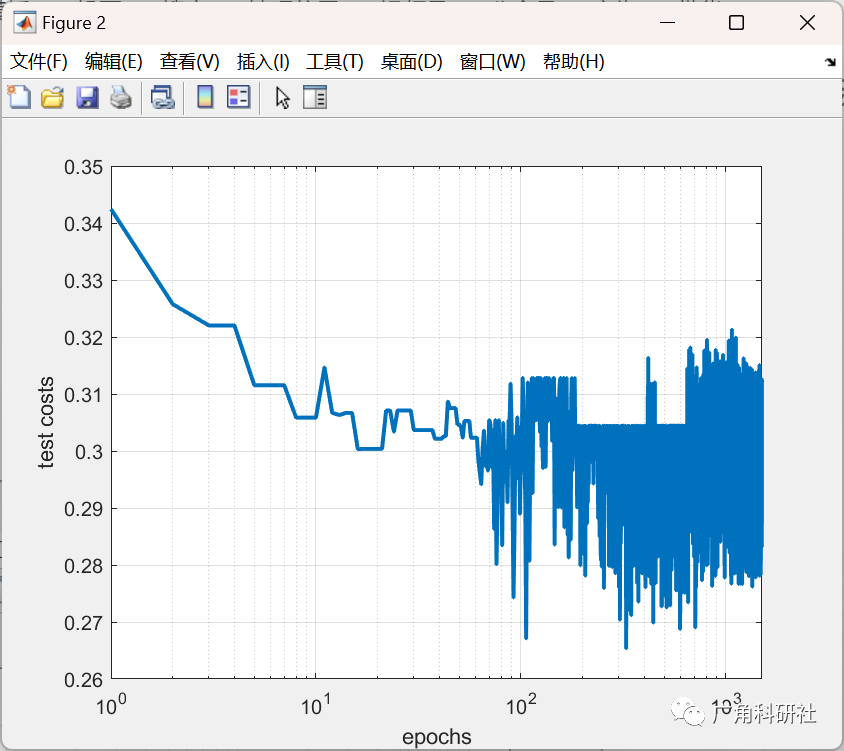
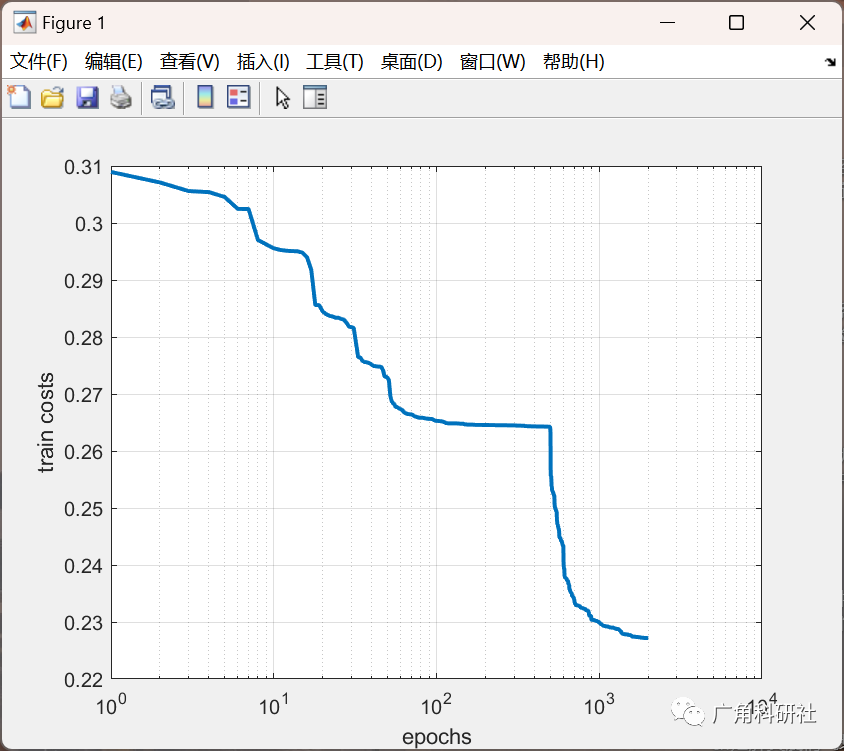
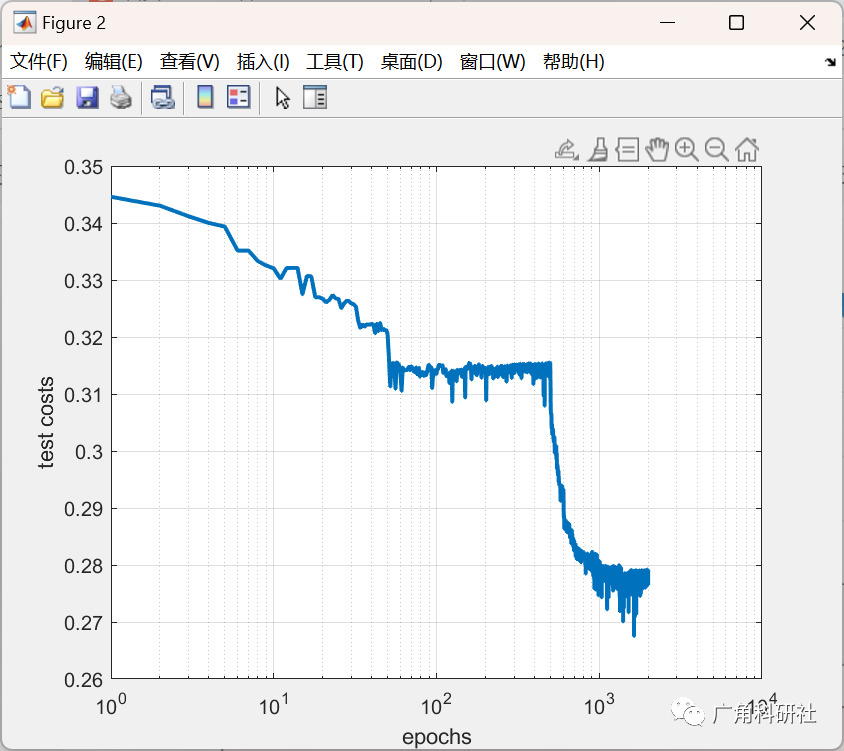
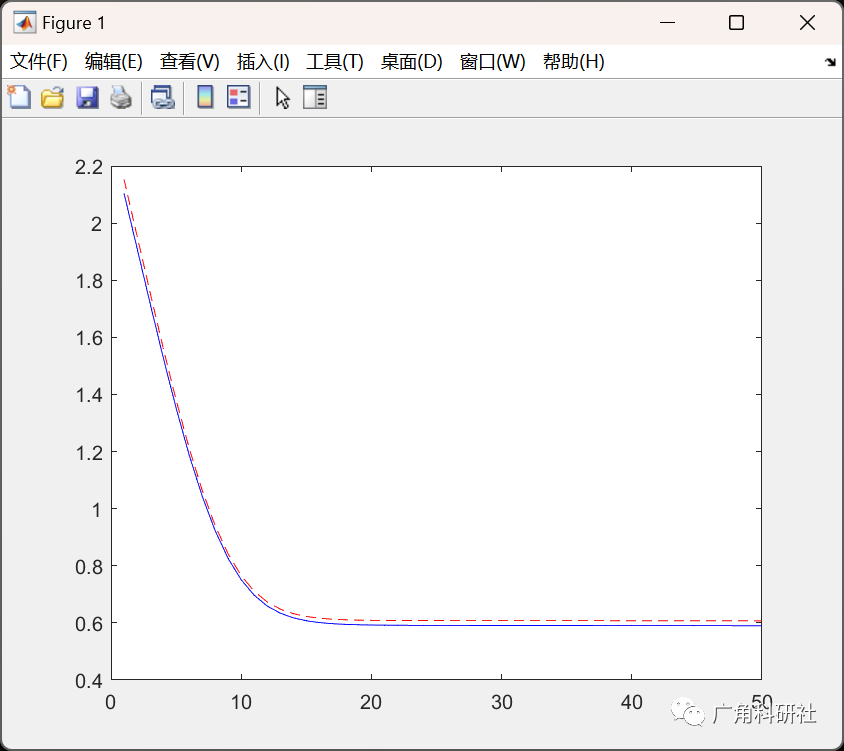
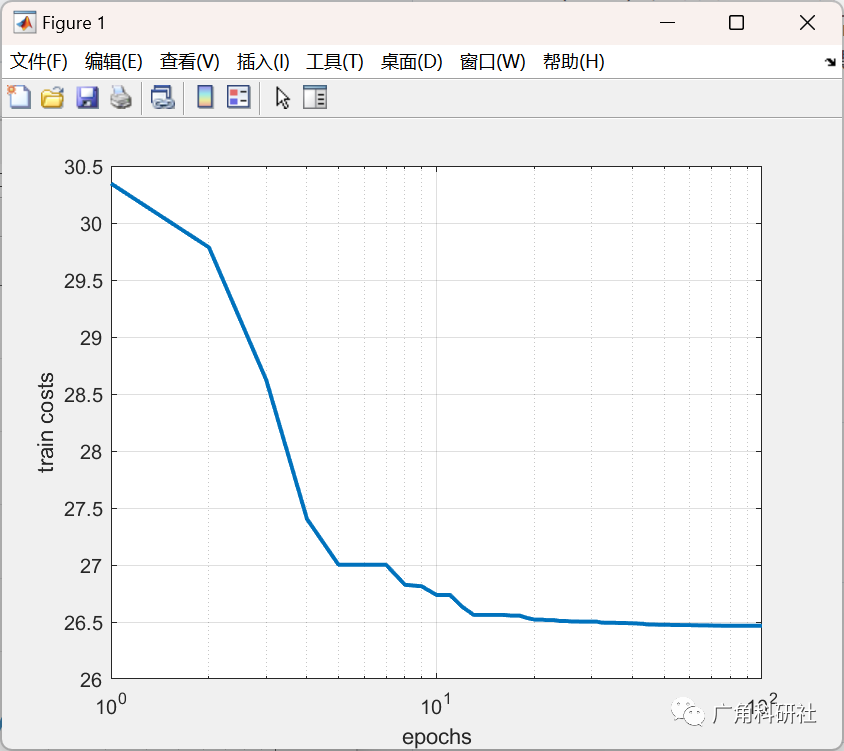
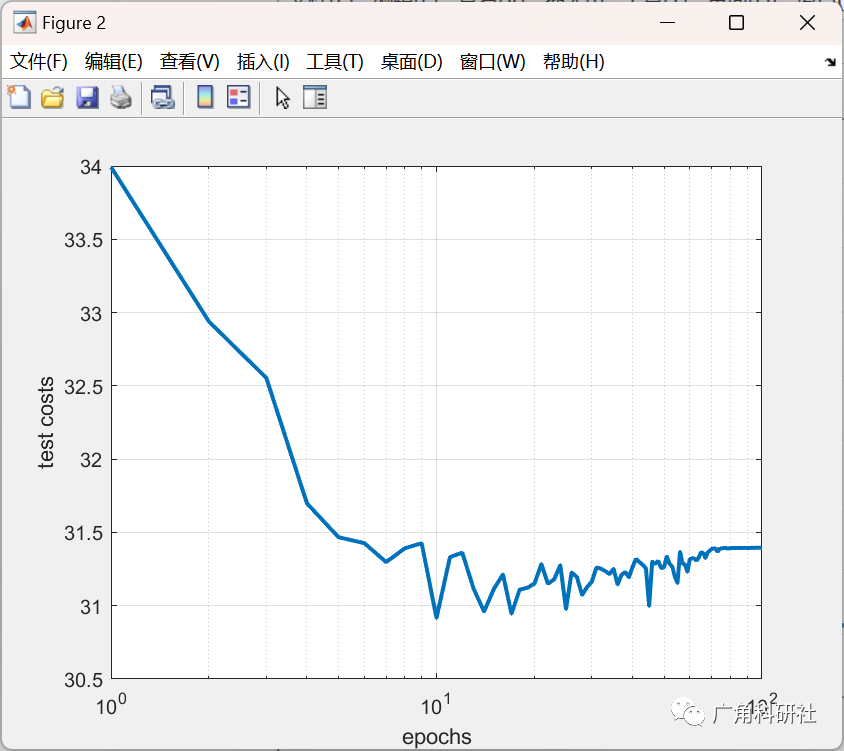
主函數部分代碼：

clc;
clear;
close all;
?
%% Problem Definition
%% loading dataset %%
load('Weight_mat.mat')
load('trainset.mat')
load('testset.mat')
?
var_num=71;            
VarSize=[1 var_num];  
VarMin=-5;        
VarMax= 5;       
%% PSO Parameters
max_epoch=100;      
ini_pop=50;        
?
% Constriction Coefficients
phi1=2.1;
phi2=2.1;
phi=phi1+phi2;
khi=2/(phi-2+sqrt(phi^2-4*phi));
w=khi;          % Inertia Weight
wdamp=0.99;        % Inertia Weight Damping Ratio
c1=khi*phi1;    % Personal Learning Coefficient
c2=khi*phi2;    % Global Learning Coefficient
?
% Velocity Limits
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
%% Initialization
?
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
?
particle=repmat(empty_particle,ini_pop,1);  
GlobalBest.Cost=inf;
Cost_Test= zeros(50,1);
for i=1:ini_pop% Initialize Positionparticle(i).Position= WEIGHTS(i ,:);% Initialize Velocityparticle(i).Velocity=zeros(VarSize);% Evaluationparticle(i).Cost=mape_calc(particle(i).Position,trainset);Cost_Test(i)=mape_calc(particle(i).Position,testset);% Update Personal Bestparticle(i).Best.Position=particle(i).Position;particle(i).Best.Cost=particle(i).Cost;% Update Global Bestif particle(i).Best.Cost<GlobalBest.CostGlobalBest=particle(i).Best;endend
?
BestCost_Train=zeros(max_epoch,1);
BestCost_Test=zeros(max_epoch,1);
[~, SortOrder]=sort(Cost_Test);
Cost_Test =Cost_Test(SortOrder);
%% PSO Main Loop
for it=1:max_epochfor i=1:ini_pop% Update Velocityparticle(i).Velocity = w*particle(i).Velocity ...+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ...+c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position);% Apply Velocity Limitsparticle(i).Velocity = max(particle(i).Velocity,VelMin);particle(i).Velocity = min(particle(i).Velocity,VelMax);% Update Positionparticle(i).Position = particle(i).Position + particle(i).Velocity;IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);% Apply Position Limitsparticle(i).Position = max(particle(i).Position,VarMin);particle(i).Position = min(particle(i).Position,VarMax);% Evaluationparticle(i).Cost = mape_calc(particle(i).Position,trainset);for l= 1:ini_popCost_Test(l)=mape_calc(particle(l).Position,testset);end[~, SortOrder]=sort(Cost_Test);Cost_Test =Cost_Test(SortOrder);BestCost_Test(it) = Cost_Test(1);% Update Personal Bestif particle(i).Cost<particle(i).Best.Costparticle(i).Best.Position=particle(i).Position;particle(i).Best.Cost=particle(i).Cost;% Update Global Bestif particle(i).Best.Cost<GlobalBest.CostGlobalBest=particle(i).Best;endendend

🎉3?參考文獻

文章中一些內容引自網絡，會注明出處或引用為參考文獻，難免有未盡之處，如有不妥，請隨時聯系刪除。

?[1]郭躍東,宋旭東.梯度下降法的分析和改進[J].科技展望,2016,26(15):115+117.

🌈4 Matlab代碼實現