滿足條件的01序列

假設長度為n個序列要求滿足題意1的前綴0的個數不能超過1的個數
將問題抽象為從(0, 0)到(n, n)
向上走一個代表這一步對應序列中的值是1，向右走代表序列中的值是0

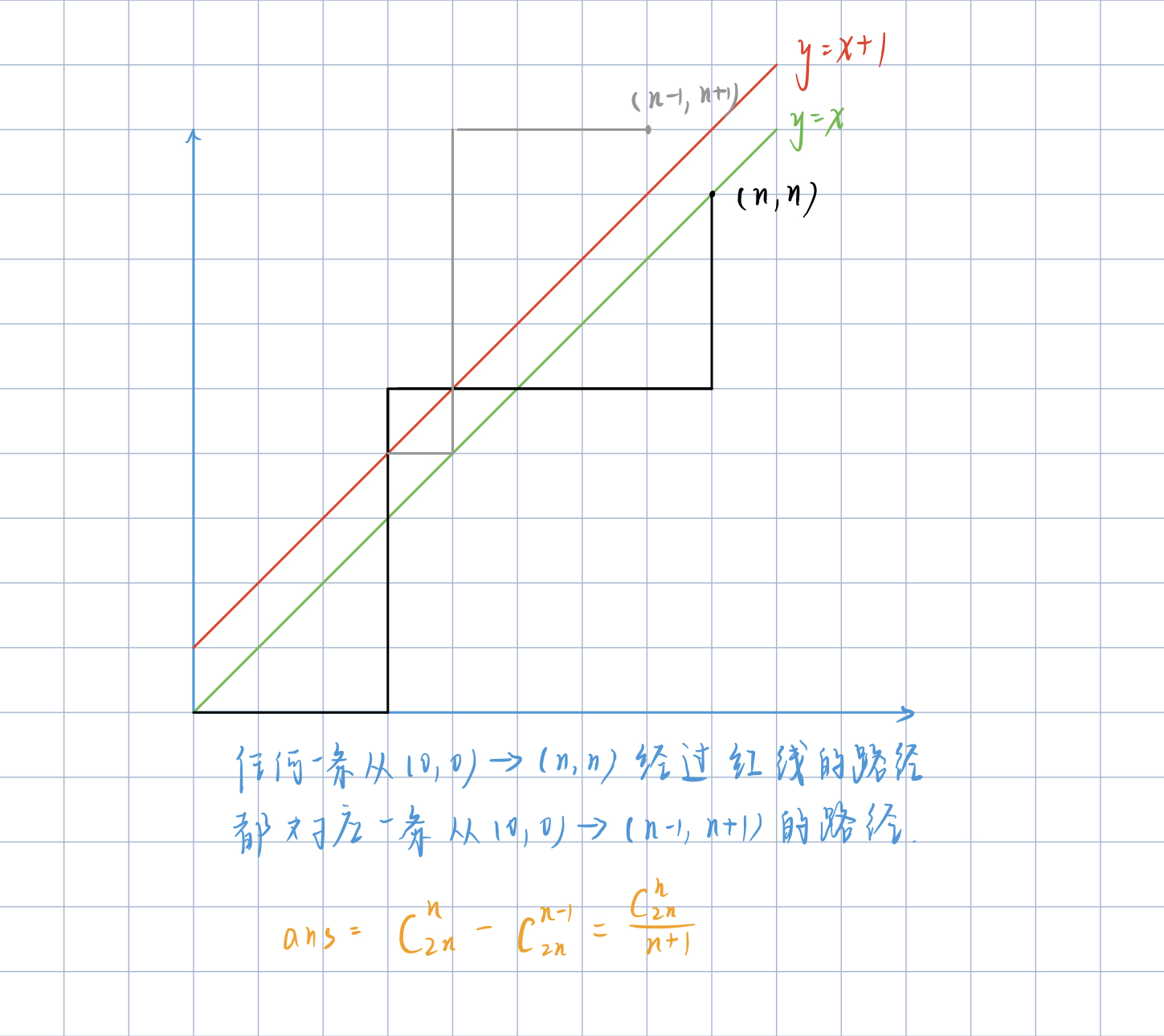
要想滿足1的前綴0的數量大于1的數量就需要滿足所有路過的途徑在y = x這個函數個下面
但是如何表達呢？
我們采用所有到(n, n)的方案的集合減去越過y = x + 1這個直線的方案集合
因為越過y = x + 1 這個直線的方案集合可以表示為從(0, 0)到(n - 1, n + 1){(n, n)關于 y = x + 1對稱的點}的方案集合
而這個答案$$C\left(\genfrac{}{}{0ex}{}{n}{2n}\right)?C\left(\genfrac{}{}{0ex}{}{n?1}{2n}\right)$$
$$=\frac{2n!}{n!?n!}?\frac{2n!}{(n+1)!(n?1)!}$$

$$=\frac{2n!?(n+1)}{n!?(n+1)!}?\frac{2n!?n}{n!?(n+1)!}$$

$$=\frac{1}{(n+1)}\frac{2n!}{n!?n!}$$
稱為卡特蘭數

$$=\frac{C\left(\genfrac{}{}{0ex}{}{n}{2n}\right)}{n+1}$$
2n是x的跨度和y的跨度的和

AcWing 889. 滿足條件的01序列

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;
int n;int qmi(int a, int b, int c)
{int res = 1;while (b){if (b & 1) res = (LL) res * a % mod;a = (LL) a * a % mod;b >>= 1;}return res;
}int main()
{scanf("%d", &n);int x = 1, y = 1;for (int i = 1; i <= 2 * n; i ++) x = (LL)x * i % mod;for (int i = 1; i <= n; i ++) y = (LL)y * i % mod;//要注意除(n + 1) 也要求逆元因為后面還要% modprintf("%lld", (LL) x * qmi(y, mod - 2, mod) % mod * qmi(y, mod - 2, mod) % mod * qmi(n + 1, mod - 2, mod) % mod);return 0;
}