今天距離2024年的AMC8美國數學競賽舉辦已不足一個月了，趕緊利用周末的時間刷刷真題，查漏補缺吧！如果您有任何關于AMC8比賽的任何問題都可以問我，關于題目的解析也可以交流。

今天我們來看看2005年AMC8競賽的五道典型考題。歡迎您查看歷史文章了解之前各年的真題解析，本系列會持續更新，直到大家參加完2024年的比賽。

好消息！為幫助孩子們更便捷地做真題，六分成長獨家將AMC8競賽2000-2023年的所有真題制作了在線版本，適合各種終端和設備利用碎片化時間，快速、反復做題，提高最后一個月的備考效率，而且這些真題文檔和在線練習題會不斷更新。

2005年AMC8數學競賽真題、考點和解析：第3題

這道題的考點是平面幾何的軸對稱。

如下圖所示，為使得圖形關于BD對稱，則編號為1,2,3,4的方塊均需要被涂成黑色，因此總共4個，選D。這種題目需要有一定的空間（平面）想象力，建議在圖上，或者電腦上截圖畫一畫，比較快。

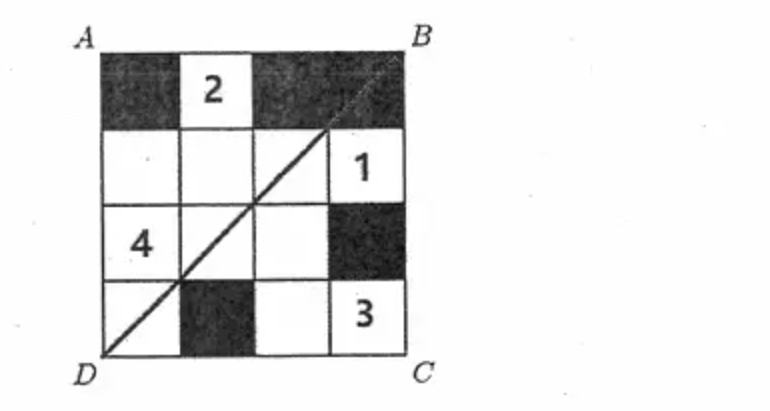
2005年AMC8數學競賽真題、考點和解析：第8題

這道題的考點是數論之奇數和偶數。

直接對各個選項逐個分析：

• 選項A：因為m是奇數，3n也是奇數，那么m+3n就是偶數。
• 選項B：因為3m和n都是奇數，所以3m-n是偶數。
• 選項C：m是奇數，那么m的平方也是奇數，3*m的平方也是奇數，所以兩項相加是偶數。
• 選項D：因為n*m和3都是奇數，所以n*m+3是偶數，則(n*m+3)的平方也為偶數。
• 選項E：因為m和n都是奇數，所以3*m*m也是奇數。符合題意，所以這道題選E。

六分成長提醒：這道題目需要了解奇數、偶數的一些特點和性質，如果記不住也沒關系，直接假設mn分別為1和3，代入各個選項用排除法也很快。

2005年AMC8數學競賽真題、考點和解析：第12題

這道題的考點是等差數列，

假設5月5日這天吃了x根香蕉，則從5月5日到5月1日，依次吃了x,x-6x-12,x-18,x-24根香蕉，它們和為100，即x+（x-6）+（x-12）+（x-18）+（x-24）=100。化簡為，5x=160，x=32，選D。

六分成長提醒：這種題目也可以直接將選項往里面代入計算，先去中間值30，然后根據計算的結果再代入另一個，也能很快得到答案。這就是選擇題的好處。

2005年AMC8數學競賽真題、考點和解析：第20題

這道題的考點是數論的倍數。

假設經過m個回合后，他們停在同一個點上，則Alice總共順時針移動了5m個點，而Bob總共逆時針移動了9m個點，因為他們停在同一個點上，所以他們移動的總點數是12的倍數，即5m+9m=14m需要是12的倍數。因為14有2這個因子，所以m必須有6這個因子，m最小為6。所以選A。

2005年AMC8數學競賽真題、考點和解析：第25題，壓軸題

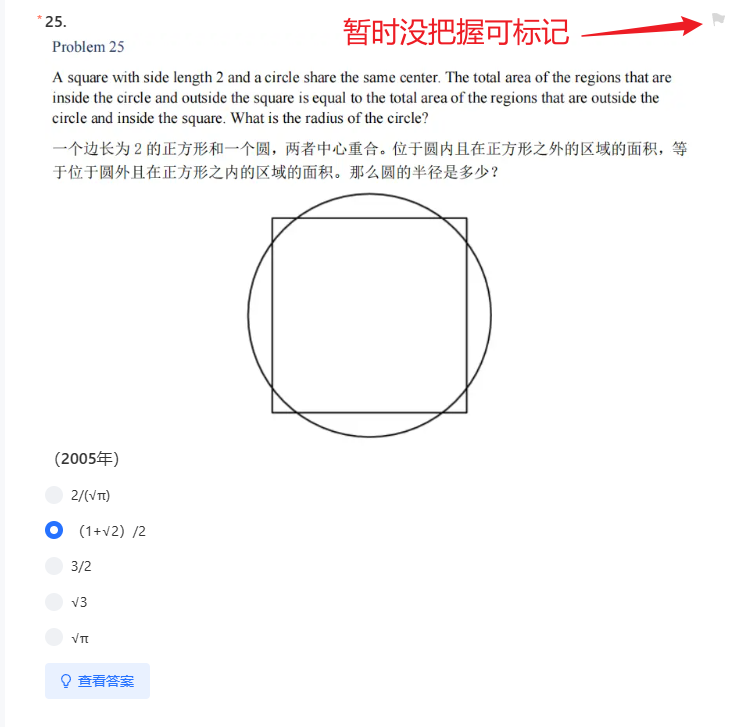
這道題的考點是平面幾何的面積。

如上圖，在圓內而在正方形之外的區域是圖中4塊黑色月牙形區域。而在正方形內圓之外的區域如圖中灰色部分所示。這2部分面積相等，意味著黑色區域從面積上恰好可以填充灰色區城，也即：圓的面積等于正方形面積。所以πr^2=2^2，計算這個算式：

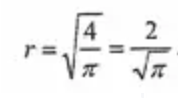
六分成長提醒：這道題目看起來很復雜，想明白了其實很簡單。不要被壓軸題嚇壞了，因為AMC8競賽的時間有限，所以題目往往不會很偏、很鉆，多思考一些巧的方法，尋找規律。當然了，這些都是建立在對題目熟悉的基礎上。

六分成長針對2024年AMC8備考資源

為幫助孩子更好地復習和備考AMC8競賽，六分成長獨家制作了豐富的在線練習真題集和備考文檔、視頻資料。無論孩子是參加了機構培訓班作為輔助學習資源，還是完全自學（實踐證明是可行的），都能大幅提高效率。如果您興趣，歡迎私信與我溝通和交流。

科學備考，利用碎片化時間再沖刺二十多天，收獲好成績！

加油！