GOOD NIGHT
前言
上一篇中,我們已經了解到了索引的基本概念和一些用法。那索引為什么會提升查詢的速度,以及索引究竟是怎么工作的呢?也許大家心里還是有一些迷茫,這一切,還要從索引背后的算法說起。
GOOD NIGHT
概述
大家知道數據庫的索引和數據,一般都是存儲在硬盤中的,這樣利于數據的持久化和永久保存。因此在我們查找數據的時候,就會產生硬盤的I/O操作。而硬盤相較于內存而言,速度是比較慢的,所以如何減少硬盤的I/O操作,就是索引背后的算法存在的意義。
GOOD NIGHT
二分法
二分法是一種常用的查找算法,相較于逐個遍歷查找而言,二分法的時間復雜度為O(log2n)。為了幫助大家理解和回憶二分查找,我畫了一張二分查找的流程圖:
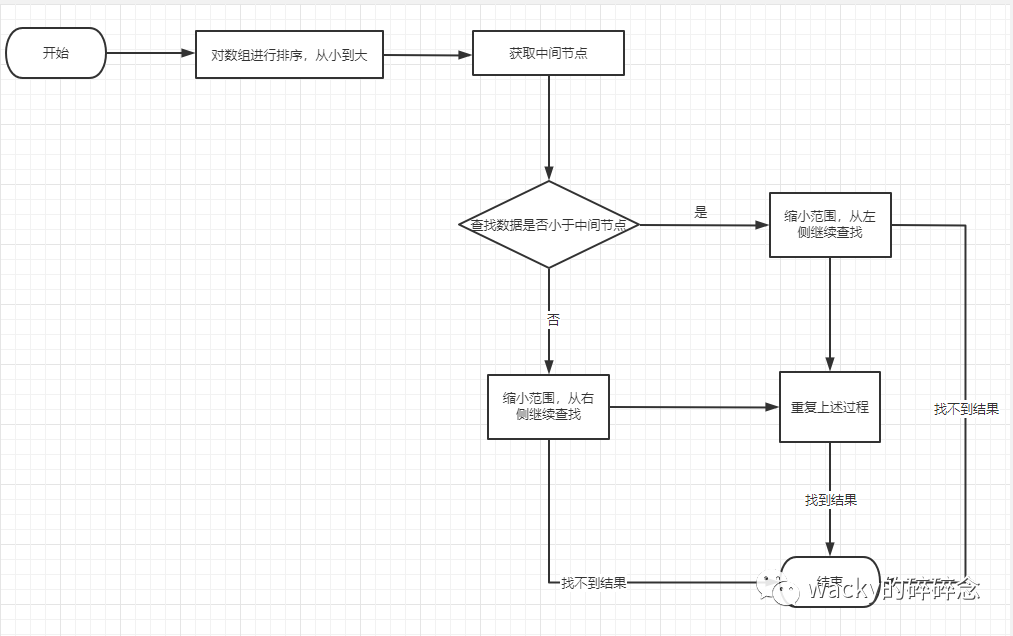
從上述流程來看,我們要事先對要查找的數組或集合進行排序,而且每次會尋找中間節點進行范圍的劃分和對數字的比較。那么我們能不能把這個過程進行簡化呢?二叉搜索樹(Binary Search Tree)會給你答案。
GOOD NIGHT
二叉搜索樹
如上文所述,二叉搜索樹的特征是有序,且預先把數據進行分段存儲,并且將中間節點作為樹的根節點,那么我們會得到如下的二叉樹結構,這里以數組[7,25,36,50,64,78,87]為例,創建出來的二叉樹如下所示:
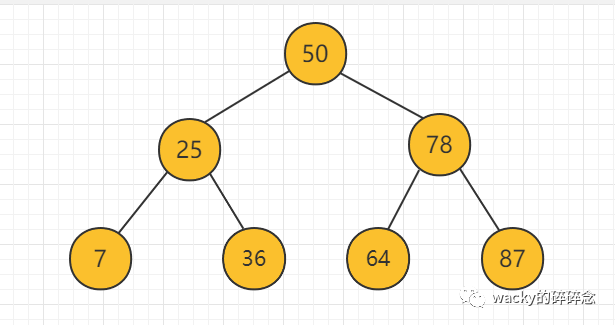
我們可以看出一些特征:對于每個節點而言,它的左孩子都小于它的父節點,而右孩子,都大于它的父節點。所以我們把這樣的二叉樹,叫做二叉搜索樹(Binary Search Tree)。
二叉搜索樹,重復利用了二分法的思想來查找數據,但有時由于構造樹時產生問題,導致同樣的數據插入順序不一樣,二叉搜索樹就會變成如下結構:
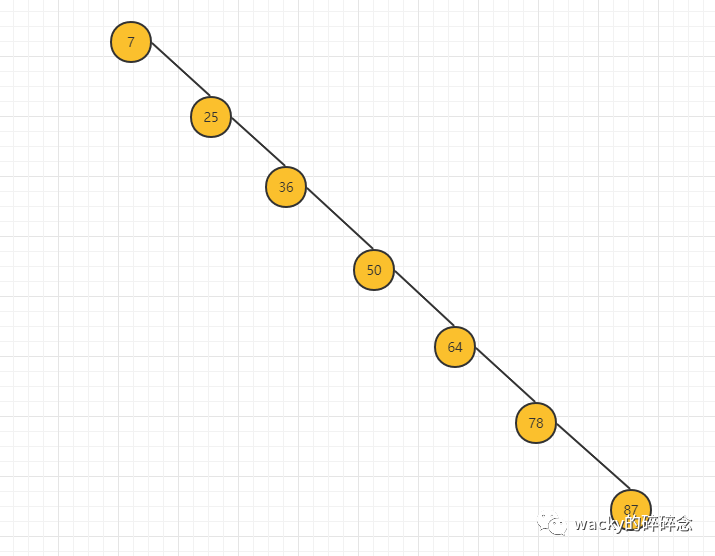
從兩張圖的比較中我們不難看出,圖一的樹高度為3,也就是最多只需要3次比較,就能找出節點,而圖二的樹的結構會變成線性,需要7次比較,查找時的復雜度也會瞬間提升為O(n)。
所以為了解決二叉樹不平衡的問題,人們又提出了新的數據結構,叫做平衡二叉搜索樹(AVL樹)。
GOOD NIGHT
平衡二叉搜索樹
剛才我們提出了,要解決二叉樹的不平衡問題,就需要一個可以在每次插入或者刪除節點時,都可以做到自動平衡的二叉樹結構,也叫平衡二叉搜索樹。
平衡二叉搜索樹的核心思想就是計算每個節點的平衡因子(balance factor),平衡因子的定義是一個節點的左孩子的高度減去其右孩子的高度,這里的高度(height)就是指從一個節點出發到達最遠葉子節點所經過的最長路徑。如我們上述的圖一中,從根節點50,到達子節點36的高度即為2。
通過上面的概念,我們可以發現,當一個節點的平衡因子絕對值大于等于1時,樹就不再平衡,所以這里平衡二叉樹還包含了一個旋轉的機制,在此不表,感興趣的同學可以自行查找進行理解。
那么我們在講了這么多之后,平衡二叉搜索樹是不是就可以作為索引背后的數據結構來進行存儲了呢?這里再使用一張圖來直觀說明一下:
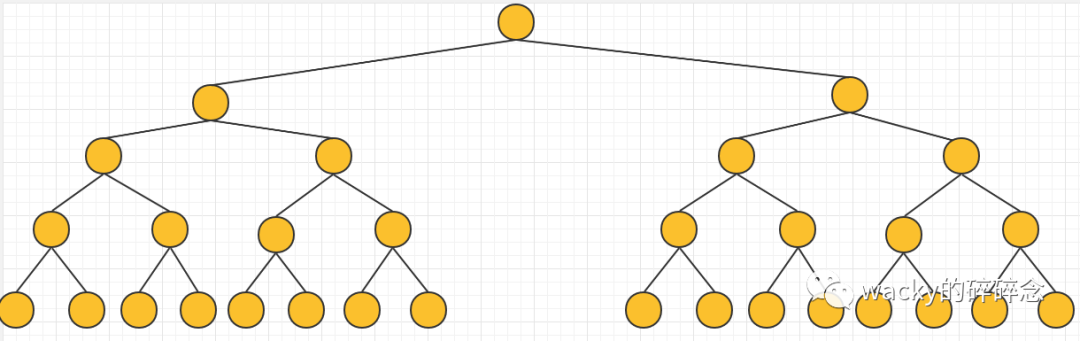
我們前文提到了查找數據是走了硬盤的I/O操作,那么對于這棵二叉樹來說,樹的高度為5,最壞的情況下,需要查找5次。這就意味著,如果樹的高度越高,那么硬盤的I/O次數也會越多。
所以我們有沒有辦法去降低樹的高度呢?可以遵循這樣的思路去思考,如果一個節點下不止2個子節點,而是多個,那么整體的高度就可以降低。比如我們將二叉樹,改為三叉樹:
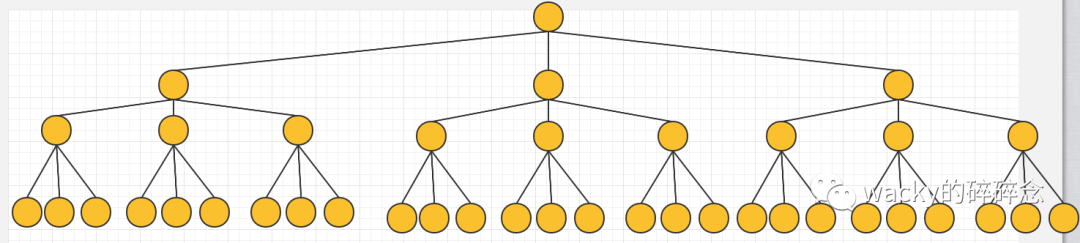
這個時候,同樣的節點數量,我們的樹高度則降為了4,也就是說,最多需要4次I/O即可找到需要查找的內容。
所以我們可以將二叉樹改為M叉樹(M>2),即一個節點下有M個子節點,這樣當數據量大小為N時,M叉樹的高度將會遠遠小于二叉樹的高度,這樣就引申出了B樹的概念。
GOOD NIGHT
什么是B樹?
B樹的英文全名為Banlance Tree,翻譯過來為平衡多路搜索樹,我們從上文中已知,當一個節點有多個子節點時,高度會下降,因此B樹很適合用于查詢,在文件系統和數據庫系統中的索引,常常會使用B樹來實現。在這里有一個概念糾正下,有些書中或博客會提到B-樹,而實際上B-樹和B樹是同一種結構,只是翻譯名稱上存在一些誤解。
B樹的結構如圖所示:
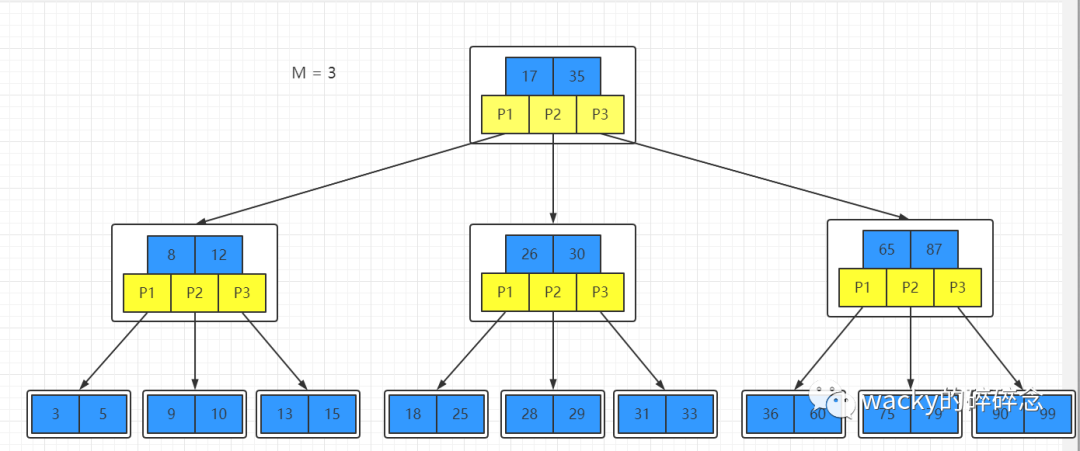
B 樹作為平衡的多路搜索樹,它的每一個節點最多可以包括 M 個子節點,M 稱為 B 樹的階。每個節點中,都存儲了關鍵字和子節點的指針。對于一個 100 階的 B 樹來說,如果有 3 層的話最多可以存儲約 100*100* 100=100 萬的索引數據。
B樹的特性有以下幾點:
1、所有節點關鍵字是按遞增次序排列,并遵循左小右大原則。
2、樹中的每個節點至多有M個子節點,即至多有M-1個關鍵字(二叉樹有2個子節點和1個關鍵字)。
3、除根節點外,其他節點至少有M/2個子節點。
4、若根節點不是葉子節點,則根節點至少有2個子節點。
5、所有葉子節點均在同一層,所以B樹是一個所有平衡因子均為0的多路查找樹。
以上圖為例,根節點中有2個關鍵字:17和35,以及3個子節點指針:P1、P2和P3。而且在第二層最左側的子節點中,有2個關鍵字8和12,包含了3個子節點。子節點1中的關鍵字為3和5,都小于8,而子節點2中的關鍵字為9和10,大于8小于12,子節點3中的關鍵字為13和15,均大于12,都符合我們上述提到的特性。
如果我們使用B樹進行查找關鍵字9,那么可以分為以下幾步:
1、先與根節點進行比較,9小于17,那么我們可以得到指針P1,繼續從子節點中進行查找;
2、在子節點中,9大于8而小于12,此時可以得到指針P2,繼續往下查找;
3、在最后一層的子節點中,找出關鍵字9,結束查找。
可以看出,相較于平衡二叉樹而言,B樹查找時的磁盤I/O要少,整體查詢效率也要高出很多。看到這里相信大家已經大致明白了索引背后的工作原理,B樹已經很適合作為索引的算法。但實際上,在MySQL中,還會使用B+樹索引,這又是為什么呢?
GOOD NIGHT
B+樹的改進
相較于B樹而言,B+樹在兩個方面又做出了改進和提升,一方面是查詢的穩定性,另一方面是查詢的效率更高。
B+樹的結構如下圖所示:
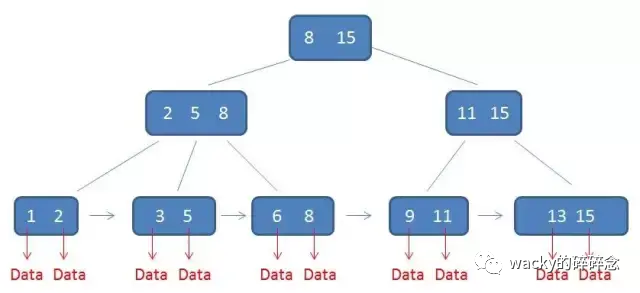
與B樹相比,B+樹的非葉子節點不保存具體的數據,而只保存關鍵字的索引,所有的數據都會保存至葉子節點。因為所有數據必須要到葉子節點才能獲取到,所以每次數據查詢的次數都一樣,這樣一來B+樹的查詢速度也就會比較穩定。
在B+樹中,非葉子節點的子節點數=關鍵字數,如上圖所示,根節點有2個關鍵字,對于的也有2個子節點。這樣的好處是一個節點可以存儲更多的關鍵字,階數會更大,高度會更低,查詢效率也就更高。
B+樹查找關鍵字的方式與B樹類似,先從關鍵字中找出范圍和指針,然后找到對應的子節點,一級一級往下查詢,直到最終的葉子節點查出所需要的數據。
由于B+樹的數據都存儲在葉子節點,所以更有利于數據庫做全表掃描,不需要像B樹一樣逐層掃描,而是直接遍歷所有的葉子節點即可。
GOOD NIGHT
總結
今天我們從最基本的二分查找開始,逐步分析了各種查找樹的工作原理和優缺點,不斷改進,從而挖掘出最終的B樹和B+樹算法,深刻理解了索引背后的工作原理。雖然傳統的二叉樹查詢的效率也很高,但是很容易增加磁盤I/O的次數,影響索引使用的效率,所以我們最終會采用降低樹高度的方式來構造索引。
在實際工作中,我們使用索引也許不會直接去編寫B樹和B+樹的算法。但是學習這些算法,會有助于我們增強邏輯思考的能力,還可以提升一些設計方面的能力,對于“修煉內功”會很有幫助,希望大家可以在這條路上持之以恒。
下一期將是索引系列的最終篇章,我們會結合實際工作中的復雜SQL場景,合理使用索引和改寫原有語句以避免全表掃描來對數據庫進行優化,敬請期待!
您的點贊和在看是我創作的最大動力,感謝支持



公眾號:wacky的碎碎念
知乎:wacky






-上篇)
![[轉]微服務的4個設計原則和19個解決方案](http://pic.xiahunao.cn/[轉]微服務的4個設計原則和19個解決方案)
oracle)

)
![[轉]GitBook使用教程收藏](http://pic.xiahunao.cn/[轉]GitBook使用教程收藏)







