一道神題,兩種神做法。
?
Description
捉迷藏 Jiajia和Wind是一對恩愛的夫妻,并且他們有很多孩子。某天,Jiajia、Wind和孩子們決定在家里玩捉迷藏游戲。他們的家很大且構造很奇特,由N個屋子和N-1條雙向走廊組成,這N-1條走廊的分布使得任意兩個屋子都互相可達。游戲是這樣進行的,孩子們負責躲藏,Jiajia負責找,而Wind負責操縱這N個屋子的燈。在起初的時候,所有的燈都沒有被打開。每一次,孩子們只會躲藏在沒有開燈的房間中,但是為了增加刺激性,孩子們會要求打開某個房間的電燈或者關閉某個房間的電燈。為了評估某一次游戲的復雜性,Jiajia希望知道可能的最遠的兩個孩子的距離(即最遠的兩個關燈房間的距離)。 我們將以如下形式定義每一種操作: C(hange) i 改變第i個房間的照明狀態,若原來打開,則關閉;若原來關閉,則打開。 G(ame) 開始一次游戲,查詢最遠的兩個關燈房間的距離。
Input
第一行包含一個整數N,表示房間的個數,房間將被編號為1,2,3…N的整數。接下來N-1行每行兩個整數a, b,表示房間a與房間b之間有一條走廊相連。接下來一行包含一個整數Q,表示操作次數。接著Q行,每行一個操作,如上文所示。
Output
對于每一個操作Game,輸出一個整數,表示最遠的兩個關燈房間的距離。若只有一個房間是關著燈的,輸出0;若所有房間的燈都開著,輸出-1。
Sample Input
8
1 2
2 3
3 4
3 5
3 6
6 7
6 8
7
G
C 1
G
C 2
G
C 1
G
Sample Output
4
3
3
4
HINT
N ≤100000, M ≤500000。
?
Solution
一道很好的裸題,可以讓你初步了解括號序列和動態點分治的用法。
先說說比較好理解的動態點分治吧:
動態點分治,顧名思義就是將點分治加上修改操作(權值修改等)并支持在線詢問。
這里說的動態不是完全動態,至少樹的整個形態是要提前知道的。
我們仔細想想最基本的點分治怎么做:
在當前的分治結構里把所有的點到分治根結點的距離處理出來,每兩條不在同一棵子樹內的距離構成一條鏈。
因此找經過分治根結點的最長的一條鏈就是到分治根結點的最長距離加上次長距離。當然這兩個距離不能在同一棵子樹內。你懂的。
然后怎么讓這個點分治“動”起來?當然是選擇數據結構啊。
清點一下,我們要維護的信息有:
①分治結構中分治根結點的某個子樹內所有的點到分治根結點的距離,目標是求最大值;
②由①得出的,分治結構中分治根結點的每個子樹內的距離最大值,目標是求最大值和次大值;
③由②得出的,每個分治結構中過分治根結點的鏈的長度,目標是求最大值(即答案)。
都是維護單點修改求整體最值!用什么?線段樹?當然是堆啊!
你可能會對①產生疑問,一個分治根結點難道要維護它的所有子樹的距離信息?一個結點開多個堆??
當然不是啊!反過來想,改成維護該分治結構中所有的點到分治父節點的距離,就完美解決了上面的問題。
除了“維護什么”,還有“怎么維護”。
這是一個典(sang)型(bing)的維護堆套堆套堆,從最低一級的堆開始,每次堆頂有變,就要往上一級更新,小C不再贅述。
手寫堆可能會寫得你欲仙欲死,這時候需要想辦法用上PQ。(如果你是Pascal黨當我沒說)
PQ是無法對堆內部的節點進行修改的,所以我們需要一些經典Trick。
用兩個堆來表示,一個用來存節點,一個用來打刪除標記。每次取top的時候把打了刪除標記的堆頂清理一下。
取次大的就把最大pop掉再push進來即可。這些具體可以看小C的代碼。
說完“怎么維護”,還有“為什么可以這樣維護”。
動態點分治的時空復雜度是以點分治為基礎的,由于分治根結點都是重心。每個結點最多只會出現在log個分治結構中。
由于所有的信息都要維護,空間和時間復雜度起步都是O(nlogn)。
如果要開線段樹,就要動態開點,空間復雜度O(nlog2n),這時就需要注意空間上的限制了。
所以無需注意標號和空間占用小的靈活的堆成為了很好的選擇。
空間復雜度O(nlogn),時間復雜度O(nlog2n)。
 發張圖輕松一下~~
發張圖輕松一下~~
?
接著小C來講講神一般的括號序列做法:
我們先引入一個大佬的博客:http://www.shuizilong.com/house/archives/bzoj-1095-zjoi2007hide-捉迷藏/
括號序列是什么?你只要寫過樹剖就會很熟悉。因為括號序列本身就是由dfs序的開頭和結尾組成的。
dfs的開頭作為左括號,結尾作為右括號,節點編號緊挨著左括號。
如下圖,可以表示為:[1[2[3][5[4]]]]。
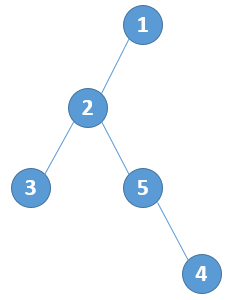
然后這樣表示有什么用呢?括號序列的作用之一就是可以配合線段樹查詢兩點之間即一條鏈上的信息。
詢問點對(1,4)的距離,1、4之間的括號串為“[2[3][5[”;
去掉數字:“[[][[”,再去掉匹配的括號:“[[[”,右括號代表向上,左括號代表向下,
這也就意味著節點1向下走3步就可以走到節點4。
所以樹上任意兩點間的距離可以用數對(a,b)表示,其中a為失配的右括號數,b為失配的左括號數,則兩點間距離為a+b。
每一段括號序列都有它的(a,b),也就是說,只要求出兩點間的括號序列的a+b即為距離。
現在進入正題了,如何用線段樹求a+b呢?
考慮左(a1,b1)右(a2,b2)兩個區間合并:若b1<a2,則為(a1+a2-b1,b2);若b1>a2,則為(a1,b2+b1-a2)。
由此我們從已知a1,b1,a2,b2可以得出以下關于新區間(a,b)的顯而易見的等式:
①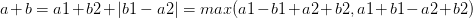
②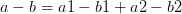
③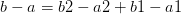
我們發現,新的a+b和a-b都是由舊的a+b和a-b通過加減運算得來。
所以設一段括號序列的a+b為plus,a-b為minus1,b-a為minus2。
進一步,題目要我們求的是兩個黑點之間的a+b,我們同樣可以通過維護以下信息求得:
①sum:表示區間中兩個黑點之間的括號序列的a+b的最大值;
②left_plus:表示區間中一個黑點左側的括號序列的b+a的最大值;
③left_minus:表示區間中一個黑點左側的括號序列的b-a的最大值;
④right_plus:表示區間中一個黑點右側的括號序列的a+b的最大值;
⑤right_minus:表示區間中一個黑點右側的括號序列的a-b的最大值;
注意上面的變量如果不存在(即黑點數不足時),都要設為-INF。
剩下的就是各種區間的合并,“兩點之間”、“左側”、“右側”實際上都是區間,根據上面的等式可以很容易求得:
①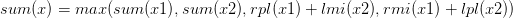
②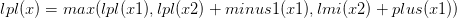
③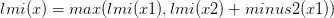
④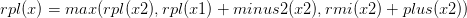
⑤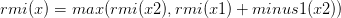
然后就開開心心地寫一寫線段樹就可以了啊。
時間復雜度O(nlogn),比動態點分治快到不知道那里去。
?
動態點分治:
#include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <vector> #define INF 0x3FFFFFFF #define MN 100005 using namespace std; struct queue {priority_queue <int> A,B;void push(int x) {if (x!=-INF) A.push(x);}void delet(int x) {if (x!=-INF) B.push(x);}int top(){while (!B.empty()&&A.top()==B.top()) A.pop(),B.pop();if (!A.empty()) return A.top(); else return -INF;}int two(){if (A.size()-B.size()<2) return -INF;register int x,y;x=top(); A.pop(); y=top(); A.push(x); return x+y;} }q[MN],q1[MN],q2; struct edge{int nex,to;}e[MN<<1]; vector <int> td[MN]; int siz[MN],hr[MN],fa[MN]; int mnz,mni,n,m,pin,gs; bool bj[MN],hu[MN];inline int read() {int n=0,f=1; char c=getchar();while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();}while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();}return n*f; }inline void ins(int x,int y) {e[++pin]=(edge){hr[x],y}; hr[x]=pin;} void getsiz(int x,int fat) {siz[x]=1;for (register int i=hr[x];i;i=e[i].nex)if (e[i].to!=fat&&!bj[e[i].to])getsiz(e[i].to,x),siz[x]+=siz[e[i].to]; } void getdp(int x,int fat,int depth,int dest) {q[dest].push(depth);td[x].push_back(depth);for (register int i=hr[x];i;i=e[i].nex)if (e[i].to!=fat&&!bj[e[i].to])getdp(e[i].to,x,depth+1,dest); } void getrt(int x,int fat,int tot) {register int i,mxz=0;for (i=hr[x];i;i=e[i].nex){if (e[i].to==fat||bj[e[i].to]) continue;getrt(e[i].to,x,tot);mxz=max(mxz,siz[e[i].to]);}mxz=max(mxz,tot-siz[x]);if (mxz<mnz) mnz=mxz,mni=x; }void dfs(int x,int fat) {bj[x]=true; fa[x]=fat;q1[x].push(0);for (register int i=hr[x];i;i=e[i].nex){if (bj[e[i].to]) continue;getsiz(e[i].to,x); mnz=n; getrt(e[i].to,x,siz[e[i].to]);getdp(e[i].to,x,1,mni);q1[x].push(q[mni].top());dfs(mni,x);}q2.push(q1[x].two()); }void setrev(int x) {register int ck,nck,cck,ncck,y,i;ck=q1[x].two();if (hu[x]) q1[x].delet(0); else q1[x].push(0);nck=q1[x].two();if (ck!=nck) q2.delet(ck),q2.push(nck);for (y=x,i=td[x].size()-1;fa[y];y=fa[y],--i){ck=q[y].top();if (hu[x]) q[y].delet(td[x][i]); else q[y].push(td[x][i]);nck=q[y].top();if (ck==nck) continue;cck=q1[fa[y]].two();q1[fa[y]].delet(ck); q1[fa[y]].push(nck);ncck=q1[fa[y]].two();if (cck!=ncck) q2.delet(cck),q2.push(ncck);} }int main() {register int i,x,y;char c[5];n=read();for (i=1;i<n;++i){x=read(); y=read();ins(x,y); ins(y,x);}for (i=1;i<=n;++i) hu[i]=true;getsiz(1,0); mnz=n; getrt(1,0,n); dfs(mni,0);m=read(); gs=n;while (m--){scanf("%s",c);if (c[0]=='C'){x=read(); setrev(x);gs+=hu[x]?-1:1; hu[x]^=1;}else if (c[0]=='G')if (gs==0) puts("-1");else if (gs==1) puts("0");else printf("%d\n",q2.top());} }
?
括號序列(畫風略清奇):
#include <cstdio> #include <algorithm> #include <cstring> #define l(a) (a<<1) #define r(a) (a<<1|1) #define O(a) (a!=-INF) #define INF 100000007 #define MM 800005 #define MN 200005 using namespace std; struct node{int lpl,lmi,rpl,rmi,sum;}T[MM]; struct meg{int x,y;}t[MM]; struct edge{int nex,to;}e[MN]; bool u[MN]; int kh[MN][2],hr[MN]; int dfn,n,m,pin,gs;inline int read() {int n=0,f=1; char c=getchar();while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();}while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();}return n*f; }inline void ins(int x,int y) {e[++pin]=(edge){hr[x],y}; hr[x]=pin;} void dfs(int x,int fat) {u[kh[x][0]=++dfn]=true;for (register int i=hr[x];i;i=e[i].nex)if (e[i].to!=fat) dfs(e[i].to,x);kh[x][1]=++dfn; }void update(node& C,const node& A,const node& B,const meg& a,const meg& b) {C.sum=max(A.sum,B.sum); if (O(A.lpl)&&O(B.lpl)) C.sum=max(C.sum,max(A.rpl+B.lmi,A.rmi+B.lpl));C.lpl=A.lpl; if (O(B.lpl)) C.lpl=max(C.lpl,max(B.lpl-a.y+a.x,B.lmi+a.y+a.x));C.rpl=B.rpl; if (O(A.lpl)) C.rpl=max(C.rpl,max(A.rpl-b.x+b.y,A.rmi+b.x+b.y));C.lmi=A.lmi; if (O(B.lpl)) C.lmi=max(C.lmi,B.lmi+a.y-a.x);C.rmi=B.rmi; if (O(A.lpl)) C.rmi=max(C.rmi,A.rmi+b.x-b.y); } inline void setin(int x) {T[x].lpl=T[x].lmi=1; T[x].rpl=T[x].rmi=0;} inline void setout(int x) {T[x].lpl=T[x].lmi=T[x].rpl=T[x].rmi=-INF;} void getcg(int x,int L,int R,int q) { if (L==R) {if (O(T[x].lpl)) setout(x); else setin(x); return;}int mid=L+R>>1;if (q<=mid) getcg(l(x),L,mid,q); else getcg(r(x),mid+1,R,q);update(T[x],T[l(x)],T[r(x)],t[l(x)],t[r(x)]); } void build(int x,int L,int R) {if (L==R){T[x].sum=-INF;if (!u[L]) t[x].x=1,setout(x); else t[x].y=1,setin(x);return;}int mid=L+R>>1;build(l(x),L,mid); build(r(x),mid+1,R);t[x].x=t[l(x)].x; t[x].y=t[r(x)].y;if (t[l(x)].y<t[r(x)].x) t[x].x+=t[r(x)].x-t[l(x)].y;else if (t[l(x)].y>t[r(x)].x) t[x].y+=t[l(x)].y-t[r(x)].x;update(T[x],T[l(x)],T[r(x)],t[l(x)],t[r(x)]); }int main() {register int i,x,y;char c[5];n=read();for (i=1;i<n;++i){x=read(); y=read();ins(x,y); ins(y,x);}dfs(1,0); build(1,1,n<<1); gs=n; m=read();while (m--){scanf("%s",c);if (c[0]=='C'){x=read(); gs+=u[kh[x][0]]?-1:1;u[kh[x][0]]^=1; getcg(1,1,n<<1,kh[x][0]);}else if (c[0]=='G')if (gs==1) puts("0");else if (gs==0) puts("-1");else printf("%d\n",T[1].sum);} }
?
Last Word
動態點分治寫起來就像吃了那啥一樣難受,還好最后把代碼壓縮到小C容易接受的地步。
括號序列是真的厲害,不知道以后能不能看到它更多的妙用。



















