通過上篇文章的學習,我們知道,相比于單個核函數,多核模型可以具有更高的靈活性。經過多個核函數映射后的高維空間是由多個特征空間組合而成的組合空間,而顯然組合空間可以組合各個子空間不同的特征映射能力,能夠將異構數據中的不同特征分量分別通過最合適的單個核函數進行映射,最終使得數據在新的組合空間中能夠得到更加準確、合理的表達,進而提高樣本數據的分類正確率或預測精度。
多核學習方法根據不同的分類標準有不同的分類方式,按照多核函數的構造方法和特點的不同,可以將多核學習方法大致分成三大類別:合成核方法、多尺度核方法、無限核方法。
一、合成核方法
把具有不同特性的多個核函數進行組合,就會得到包含各個單核函數的總體特性的多核函數。多核函數形成的方式本身就使得多核函數具有更加準確、更加強大的映射能力或者分類能力,特別是對于實際應用中樣本數據具有比較復雜分布結構的分類、回歸等學習問題,多核學習的優點非常明顯。
(1)多核線性組合合成方法
多核線性組合方法是將基本核函數進行線性組合,用表達式可以如下所示描述:
假設變量 x,z ∈X,其中 X 屬于 R(n)空間,非線性函數Φ能夠實現輸入空間 X到特征空間 F 的映射,其中 F ∈R(m),m>>n。假設已知的基本核函數為k (x,z) ,再將其進行歸一化為?k(x,z),則可以通過以下方式進行線性組合得到多核函數:
直接求和核其中, 其中 ?k(x,z) 為第 i 個基本核函數。
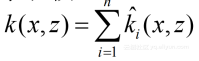
加權求和核,其中βi為第 i 個核函數的權值。

多項式加權擴展核,其中kp(x,z)是k (x,z) 的多項式擴展。
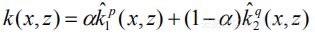
(2)多核擴展合成方法
上述描述的多核組合方法主要是基于將基本核函數直接求和或者加權求和的思想實現多個核函數的結合,但這樣的方法最大的問題是可能丟失原始數據的某些特征信息,比如數據分布的某塊區域包含很多信息并且是多變的,當使用平均或者加權平均的方式將該部分數據“平滑”之后,能夠表示多變信息的數據很有可能被不用的核函數給平滑掉,有可能導致最終的特征信息不完整,降低分類器的分類能力和準確性,基于上述考慮,產生了將原有多核矩陣進行擴展合成的方法,也就是最終能夠使用的多核矩陣是由原先的單個核矩陣和其核矩陣共同構成的。因此, 原始核函數的性質得以保留。該合成核矩陣的形式為:
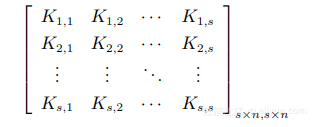
可以看出, 原始核矩陣位于新矩陣的對角線上. 其他所有元素是定義為 (Kp,p0 )i,j = Kp,p0 (xi , xj ) 的兩個不同核矩陣的混合, 可由如下公式求得 (以兩個 高斯核為例):
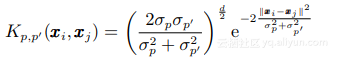
很明顯,當p = p 0 時, Kp,p ≡ Kp.實驗結果顯示,當數據集具有變化的局部數據分布時,這種合成核方法將是更好的選擇.此外, 通常核組合方法在很大程度上依靠訓練數據,并且必須通過學習獲取一些權系數,以標識每個核的重要性.
(3)非平穩多核學習
前邊的多核線性組合方法都是對核函數的平穩組合, 即對所有輸入樣本, 不同的核對應的權值是不變的, 無形中對樣本進行了一種平均處理.Lewis 提出了一種多核的非平穩組合方法, 對每個輸入樣本配以不同的權值系數.如常規 SVM判別函數為:
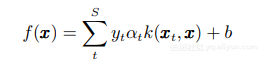
引入不同的加權系數, 典型的合成核 SVM 的判別函數可以改寫為:
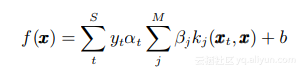
在最大熵判別框架下, 通過使用一種大間隔隱變量生成模型, 使得隱參數估計問題可以通過變化邊界和一個內點優化過程來表示, 并且相應的參數估計可以通過快速的序列最小優化算法實現。
(4)局部多核學習
針對多核學習在整個輸入空間中對某個核都是分配相同權值的問題, 利用一種選通模型 (Gating model) 局部地選擇合適核函數, 提出了一種局部多核學習算法. 在SVM 框架下, 其判別函數形如:
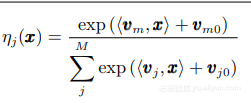
這里的vm 和vm0 是選通模型參數, 可以在多核學習過程中通過梯度下降法獲得.將局部選通模型和基于核的分類器相結合,優化問題可以用一種聯合的方式加以解決。
二、多個尺度的多核學習: 多尺度核方法
合成核方法雖然有了一些成功應用,但都是根據簡單核函數的線性組合, 生成滿足Merce條件的新核函數;核函數參數的選擇與組合沒有依據可循,對樣本的不平坦分布仍無法圓滿解決,限制了決策函數的表示能力。在此情況下,出現了多核學習的一種特殊化情形,即將多個尺度的核進行融合。這種方法更具靈活性, 并且能比合成核方法提供更完備的尺度選擇.此外,隨著小波理論、多尺度分析理論的不斷成熟與完善,多尺度核方法通過引入尺度空間,使其具有了很好的理論背景。
多尺度核方法的基礎就是要找到一組具有多尺度表示能力的核函數. 在被廣泛使用的核函數中, 高斯徑向基核是最受歡迎的, 因為它們具有通用普遍的近似能力,同時它也是一種典型的可多尺度化核. 以此核為例,將其多尺度化 (假設其具有平移不變性):
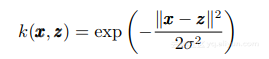
其中, σ1 < · · · < σm. 可以看出, 當σ較小時, SVC可以對那些劇烈變化的樣本進行分類; 而當σ較大 時, 可以用來對那些平緩變化的樣本進行分類, 能得到更優的泛化能力. 具體實現時,σ的取值可以借鑒 小波變換中尺度變化的規律, σ可由下式定義:
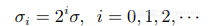
對多尺度核的學習方法:
很直觀的思路就是進行多尺度核的序列學習. 多尺度核序列合成方法。簡單理解就是先用大尺度核擬合對應決策函數平滑區域的樣本, 然后用小尺度核擬合決策函數變化相對劇烈區域的樣本, 后面的步驟利用前面步驟的結果,進行逐級優化,最終得到更優的分類結果。考慮一個兩尺度核 k1 和 k2 合成的分類問題. 我們要得到合成的決策函數:
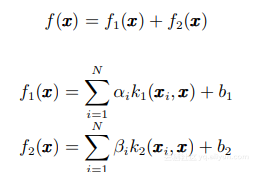
設想k1是一個大尺度的核函數(如σ較大的徑 向基函數),相關的核項系數 αi 選擇那些決策函數f(x)光滑區域對應的支持向量而k2是小尺度核函數,核項系數βi選擇那些決策函數f(x)劇烈變化區域對應的支持向量.具體方法是: 首先通過大尺度的單核 k1 構造函數f1(x),這樣,該函數可以很好地擬合光滑區域,但在其他地方存在顯著誤差,可以使用相對較小的松弛因子來求取αi;然后,在 f1(x)基礎上使用小尺度的核 k2 構造 f2(x), 使得聯合函數 f1(x) + f2(x)比f1(x) 具有更好的擬合性能.這種方法實際上是多次使用二次規劃以實現參數的獲取,運算復雜度較高, 同時支持向量的數量大量增加。
三、從有限向無限核的擴展 : 無限核方法
合成核與多尺度核方法都是在有限個核函數線性組合前提下加以討論的。但對一些大規模問題,基于有限個核的多核處理方法不一定有效,多核融合的決策函數的表示能力也不能達到處處最優。 此外,在一個多尺度核函數族中, 有限個核函數的選 擇并不唯一,并且其不能完備地表征這個核函數族.因此,將有限核向無限核的擴展也是一個重要的方向。
無限核是從由多個基本核函數的合法集合所構成的一個凸殼中找到某個核,使其能最小化凸正則化函數.與其他方法相比,這個方法有一個獨有的特征, 即上述基本核的個數可以是無限多個, 僅僅需要這些核是連續參數化的.此外,用半無限規劃解決來自通用核類型的核函數學習問題。
IKL 可以比SVM/MKL 大大提高分類正確率, 在這些情況下,IKL 能保持它的實用性, 而交叉驗證和 MKL 都是不實用的。
原文發布時間為:2018-08-06
本文作者:Walker
本文來自云棲社區合作伙伴“磐創AI”,了解相關信息可以關注“磐創AI”。





![[HDU517] 小奇的集合](http://pic.xiahunao.cn/[HDU517] 小奇的集合)













