今天來學習歸并排序算法。

分而治之

歸并算法的核心思想是分而治之，就是將大問題轉化為小問題，在解決小問題的基礎上，再去解決大問題。將這句話套用到排序中，就是將一個大的待排序區間分為小的待排序區間，對小的排序區間進行排序，然后再去解決大區間的排序，而對小區間進行排序的時候可以繼續使用該方法，將小的待排序區間分為小小的待排序區間... ...依次往復。最終將排序區間分到只有一個元素，這個時候，因為一個元素已經就是排好序的，無需繼續切分了，然后我們再依照此結果去解決大區間的排序。

假設我們現在有[53, 89, 32, 45, 67, 2, 32, 89, 65, 54]這么一個數組，我們要對它進行歸并排序(從小到大排序，此文中均為從小到大排序)，整體的過程如下圖所示：

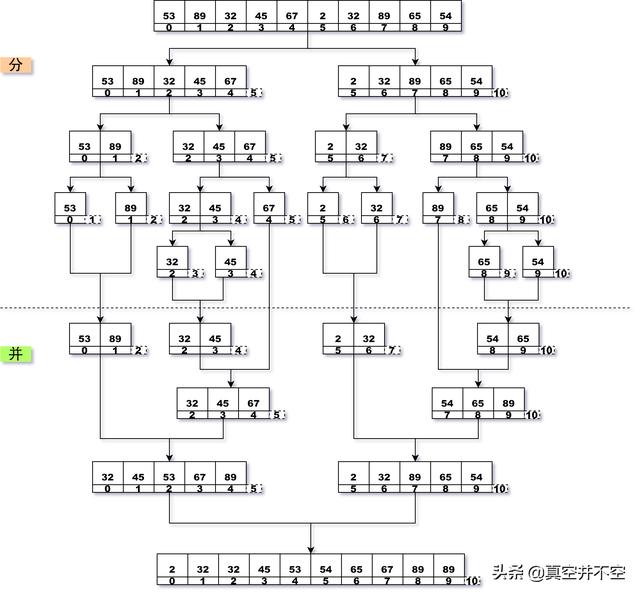
歸并排序算法完整過程

整個算法分為兩大階段，分割階段和歸并階段。

分割階段

1. [53, 89, 32, 45, 67, 2, 32, 89, 65, 54]分為[53, 89, 32, 45, 67]和[2, 32, 89, 65, 54]。

2. [53, 89, 32, 45, 67]分為[53, 89]和[32, 45, 67]， [2, 32, 89, 65, 54]分為[2, 32]和[89, 65, 54]。

4. ... ...

5. 數組分割完畢，所有小數組依次為[53]，[89] ，[32] ，[45]，[67]，[2]，[32]，[89]，[65]，[54]。

歸并階段

1. [53]，[89]歸并為[53, 89]，[32] ，[45]歸并為[32, 45]，[2]和[32]歸并為[2, 32]，[65]和[54]歸并為[54, 65](這一步中，[67]和[89]沒有歸并，因為在最后一步分割過程中，它們被單獨分開了)。

2. [32, 45]和[67]歸并為[32, 45, 67]，[89]和[54, 65]歸并為[54, 65, 89]。

3. [53, 89]和[32, 45, 67]歸并為[32, 45, 53, 67, 89]，[2, 32]和[54, 65, 89]歸并為[2, 32, 54, 65, 89]。

4. [32, 45, 53, 67, 89]和[2, 32, 54, 65, 89]歸并為[2, 32, 32, 45, 53, 54, 65, 67, 89, 89](其中兩個32和兩個89，在歸并的過程中保留它們的原始順序)。

整個分而治之的過程我們已經清楚了，可還有一個問題沒有解決，就是具體應該怎么去歸并呢，即如何將兩個排序子數組(或子區間)合并為大的排序好的數組(或區間)呢？

我們可以先舉個簡單的例子：現在有[2]和[1]兩個數組，我們如何把它們合并為[1, 2]整個數組呢？很簡單，我們首先會把這兩個元素取出來，對比一下，取出2和1，我們一對比，發現1小于2，所以我們在結果數組中先放入1，然后再放入2。可以發現，我們就是將兩個子數組中的元素取出來比較了一下，哪個小就把哪個先放入結果數組中。

從上面的例子中我們可以得到大概的思路就是，針對兩個有序的子數組(或子區間)，我們可以從頭依次取兩個子數組(或子區間)的首元素(因為從小到大排序后首元素肯定最小)，然后作對比，把小的元素放入結果數組中，并且這個元素在下次選取的時候剔除，下一個元素也應用同樣的方法得到，放入結果數組中，依次進行，直到兩個數組的元素都取完為止，如果發現其中一個子數組(或子區間)率先取完，就直接將另外一個子數組(或子區間)中剩下的元素全部放入結果數組中即可。具體步驟描述如下：

1. 判斷兩個子數組(或子區間)是否含有剩余元素，如果都有剩余元素，進入第2步；如果只有一個有剩余元素，進入第5步；如果沒有，則退出。

2. 取出左子數組(或左子區間)的首個元素和右子數組(或右子區間)的首個元素。

3. 兩個元素對比，將小的元素放入結果數組，并且從對應數組中剔除該元素。

4. 回到第1步(上一步選中的元素已被剔除)。

5. 將剩余元素直接全部放入結果數組中，退出(因為元素全部移動完畢)。

其中，剔除這一步在代碼實現中可看成索引的移動。

上述這個過程我們取[53, 89]和[32, 45, 67]這兩個子數組的合并來描述一下，如圖所示：

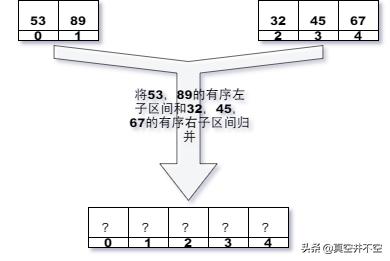
歸并

1. 取出左子數組中的首個元素53和右子數組中的首個元素32，兩個作對比，發現32 < 53，所以我們將32放入結果數組：

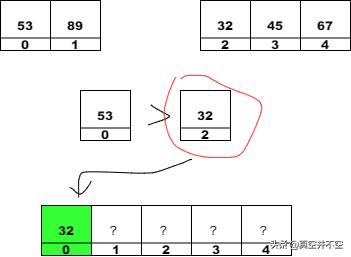
2. 取出左子數組中的首個元素53和右子數組中的首個元素45，兩個作對比，發現45 < 53，所以我們將45放入結果數組：

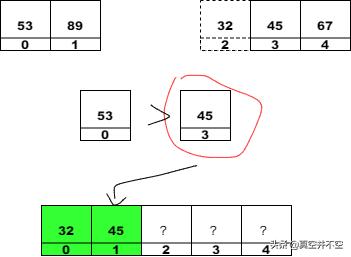
3. 取出左子數組中的首個元素53和右子數組中的首個元素67，兩個作對比，發現53 < 67，所以我們將53放入結果數組：

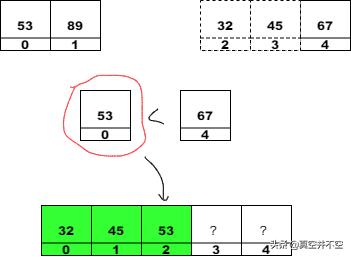
4. 取出左子數組中的首個元素89和右子數組中的首個元素67，兩個作對比，發現67 < 89，所以我們將67放入結果數組：

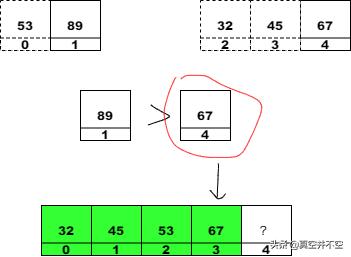
5. 此時我們發現只有左子數組存在元素，所以直接將左子數組的剩下所有元素，此時只有89放入結果數組：

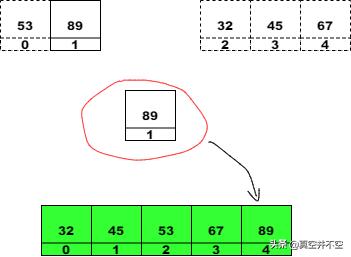
6. 至此，所有元素移動完畢，退出。

通過以上分析，我們可以知道整個歸并排序算法總體上分為一個整體的大邏輯(分而治之)和一個局部的小邏輯(歸并)，在大邏輯(分而治之，將整個數組切分，并在確認子數組有序后歸并)的基礎上，結合使用小邏輯(歸并，將兩個有序子數組歸并為一個大的有序數組)即可實現對整個數組的排序。

最終代碼實現如下：

/** * 數組的歸并排序算法 * * @param nums 數組 * @param lo 區間的lo索引(包含) * @param hi 區間的hi索引(不包含) */public static void mergeSort(int[] nums, int lo, int hi) {    // 數組為null則直接返回    if (nums == null) {        return;    }    // 索引檢查    if (lo < 0 || nums.length <= lo) {        throw new IllegalArgumentException("lo索引必須大于0并且小于數組長度，數組長度：" + nums.length);    }    if (hi < 0 || nums.length < hi) {        throw new IllegalArgumentException("hi索引必須大于0并且小于等于數組長度，數組長度：" + nums.length);    }    if (hi <= lo) {        // lo索引必須小于hi索引(等于也不行，因為區間是左閉右開，如果等于，區間內元素數量就為0了)        throw new IllegalArgumentException("lo索引必須小于hi索引");    }    if (lo + 1 >= hi) {        // 區間元素個數最多為1        // 無需排序        return;    }    int mid = (lo + hi) / 2;    // 對左子區間排序    mergeSort(nums, lo, mid);    // 對右子區間排序    mergeSort(nums, mid, hi);    // 對兩個排序好的子區間歸并，得到一個整體有序的區間    merge(nums, lo, mid, hi);}public static void merge(int[] nums, int lo, int mid, int hi) {    // 這里不用檢查索引，調用方已經決定了索引是有效的    // 結果區間和右子區間使用原有數組    // 左子區間使用臨時數組(因為結果區間可能會覆蓋左子區間的元素，所以需要開辟新數組保存)    int leftLen = mid - lo;    int[] left = new int[leftLen];    System.arraycopy(nums, lo, left, 0, leftLen);    // 左子區間索引    int leftIdx = 0;    // 右子區間索引    int rightIdx = mid;    // 結果區間索引    int resultIdx = lo;    while (true) {        if (leftIdx < leftLen && rightIdx < hi) {            // 兩個子區間都存在元素            // 取兩個子區間的有效首元素對比            if (left[leftIdx] <= nums[rightIdx]) {                // 左子區間首元素小于右子區間首元素                // 將左子區間首元素放到結果位置，同時更新索引位置                nums[resultIdx++] = left[leftIdx++];            } else {                // 右子區間首元素小于左子區間首元素                // 將右子區間首元素放到結果位置，同時更新索引位置                nums[resultIdx++] = nums[rightIdx++];            }        } else {            if (leftIdx < leftLen) {                // 左子區間還有剩余元素                // 直接將左區間所有元素一起移動到結果位置                System.arraycopy(left, leftIdx, nums, resultIdx, leftLen - leftIdx);            } else {                // 右子區間還有剩余元素                // 因為經過上一次判斷，左子區間和右子區間只會有一個存在剩余元素                // 直接將右區間所有元素一起移動到結果位置                System.arraycopy(nums, rightIdx, nums, resultIdx, hi - rightIdx);            }            // 全部元素移動完畢，退出            break;        }    }}

測試代碼如下：

List numList = IntStream.range(0, 10).boxed().collect(Collectors.toList());for (int i = 1; i <= 5; i++) {    System.out.println("================第" + i + "次================");    Collections.shuffle(numList);    int[] nums = new int[numList.size()];    for (int j = 0; j < nums.length; j++) {        nums[j] = numList.get(j);    }    System.out.println("排序前：" + Arrays.toString(nums));    mergeSort(nums, 0, numList.size());    System.out.println("排序后：" + Arrays.toString(nums));}

運行結果如下：

================第1次================排序前：[8, 4, 1, 6, 7, 0, 5, 9, 2, 3]排序后：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]================第2次================排序前：[2, 5, 6, 7, 9, 4, 3, 1, 0, 8]排序后：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]================第3次================排序前：[2, 0, 5, 6, 7, 3, 4, 9, 8, 1]排序后：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]================第4次================排序前：[4, 0, 3, 8, 1, 5, 9, 7, 2, 6]排序后：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]================第5次================排序前：[7, 9, 8, 2, 0, 5, 6, 3, 4, 1]排序后：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

測試代碼中5次隨機將數組打亂，然后運行我們的歸并排序算法，均得到有序結果，符合我們的預期。